Abstract
The work or energy W, which is necessary to move a unit mass in a force field \(\varvec{F}\) or \(\varvec{G}\), is usually depending on the chosen path \(\varvec{\Psi }(t)\) between the points \(\varvec{A}\) and \(\varvec{B}\). The work is then evaluated by a line integral
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Author information
Authors and Affiliations
Corresponding author
Appendices
Exercises
Line Integral within a Vector Field
-
27.
A unit mass is moved in the two-dimensional vector field \( \varvec{F}= \begin{pmatrix} \frac{1}{1+y^2},&-x \end{pmatrix}^\top \) along the curve \( \varvec{\Psi } (t)= \begin{pmatrix} \text {e}^{2t}-\text {e}^{t},&\text {e}^{t} \end{pmatrix}^\top \).
-
(a)
Determine the work/energy for moving a unit mass along the curve between \(t\in [0,\ln 4].\)
-
(b)
Verify – without using the curl operator – that the work is path-dependent and so the vector field cannot be conservative.
-
(a)
-
28.
Calculate the work for moving a unit mass along the curve \( \varvec{\Psi }(t) = \begin{pmatrix} \frac{3t^2}{1+t^3},&\frac{3t}{1+t^3} \end{pmatrix}^\top \) for \( t \in [0,\infty [ \) in the force field \(\varvec{F} = \begin{pmatrix}-y,&x \end{pmatrix}^\top \).
-
29.
Calculate the work for moving a unit mass in the non-conservative vector field
$$\begin{aligned} \bar{\varvec{G}}(r,\vartheta ,\lambda )&= \frac{1}{r^2} \,\hat{\varvec{h}}_r - \cos \lambda \sin \vartheta \,\hat{\varvec{h}}_\vartheta +\sin 2\vartheta \sin \lambda \,\hat{\varvec{h}}_\lambda \end{aligned}$$(of exercise 19) along the intersection curve of a circular cylinder \(\mathcal {Z}\! :\!\Big \{\varvec{x}\in \mathbb {R}^3\! :\! \left( y-\frac{1}{2}\right) ^2\!+x^2\! =\! \frac{1}{4}\!\Big \}\) and the surface \(\Sigma _+\! =\! \Big \{\varvec{x}\in \mathbb {R}^3\! :\! \Vert \varvec{x}\Vert {\hbox { = 1}}, z\,{\ge }\, 0\Big \}\).
-
30.
Calculate the energy W for moving a unit mass in the vector field \(\varvec{F} = \begin{pmatrix} x,&y,&y\ln (x^2+y^2) \end{pmatrix}^\top \) along the curve \(\varvec{\Psi }(t)\) which is defined by the intersection of the plane \(\mathcal {E} : 1-\frac{x}{2} = z\) and the cylinder \(\mathcal {Z}\!:\!\Big \{\varvec{x}\in \mathbb {R}^3: x^2+y^2 = R^2\Big \}.\) Evaluate the energy for the two cases \(R= 1\) and \(R = 2\).
Potential and Gradient
-
31.
Calculate the energy W for moving a unit mass along the curve \(\varvec{\Psi }(t) = \begin{pmatrix} t^2,&\cos t^2,&t^2 \end{pmatrix}^\top \) with \(t \in \left[ 0,\sqrt{\pi }\right] \) in the radial-dependent vector field \(\varvec{G}(r,\vartheta ,\lambda ) = \dfrac{(r+1)(3r-1)}{r^3+r^2-r+100}\,\hat{\varvec{h}}_r\) in spherical coordinates.
-
32.
Determine the parameters \(\{a,b,c, d\}\) in such a way that the vector field
$$\begin{aligned}\varvec{F} = \frac{1}{(x+y+z)^3}\begin{pmatrix} x+y-3z\\ ax+by+cz\\ dx+3y-z \end{pmatrix}\end{aligned}$$is conservative and derive also the corresponding potential.
-
33.
The vector field
$$\begin{aligned} \varvec{G}(r,\vartheta ,\lambda ) = \text {e}^{\lambda +\vartheta }\,\hat{\varvec{h}}_r + \Big (\text {e}^{\lambda +\vartheta }+\frac{2}{r}\Big )\,\hat{\varvec{h}}_\vartheta + \frac{\text {e}^{\lambda +\vartheta }+\frac{1}{r}}{\sin \vartheta }\,\hat{\varvec{h}}_\lambda \end{aligned}$$is given in spherical coordinates. Find the corresponding potential.
-
34.
A vector field is given in cylindrical coordinates by
$$\begin{aligned}\varvec{G}_\eta (\rho ,\phi , z) =&-\sin \phi \tanh \rho \,\hat{\varvec{h}}_\rho + \Big (\ln | \cosh z| + \eta \ln |\cosh \rho |\Big )\frac{\cos \phi }{\rho }\,\hat{\varvec{h}}_\phi \\&+\sin \phi \tanh z\,\hat{\varvec{h}}_z\end{aligned}$$with \(\eta \in \mathbb {R}\).
-
(a)
Determine the parameter \(\eta \) in such a way, that the vector field is conservative and find the corresponding potential \(\Phi (\rho ,\phi , z)\).
-
(b)
Find the work for moving a unit mass along the curve \(\varvec{\Psi } = 2\,\hat{\varvec{h}}_\rho +2\,\hat{\varvec{h}}_z\) with \(\phi \equiv t\) and fix the parameter to \(\eta = 0\) and \(\eta =- 1\), respectively.
-
(a)
-
35.
Parabolic coordinates are given by the relationship
$$\begin{aligned} x = \alpha \beta \cos \gamma ,\qquad y = \alpha \beta \sin \gamma ,\qquad z&= \frac{\alpha ^2-\beta ^2}{2} \end{aligned}$$with \(\gamma \in [0,2\pi ],\quad \alpha ,\beta \in \mathbb {R}^+\).
-
(a)
Determine the ‘frame vectors’ \(\,\hat{\varvec{h}}_{q_i}\) and the gradient in this system.
-
(b)
Assume the vector field
$$\begin{aligned} \varvec{G}(\alpha ,\beta ,\gamma ) = \frac{1}{\alpha ^2} \,\hat{\varvec{h}}_\alpha -\frac{1}{\alpha \beta } \,\hat{\varvec{h}}_\beta +\frac{1}{\alpha \beta } \,\hat{\varvec{h}}_\gamma \end{aligned}$$to be conservative and calculate the corresponding potential \(\Phi \).
-
(a)
-
36.
A modified spherical coordinate system is defined by
$$\begin{aligned}x&= {\sqrt{2}}^\alpha \Big (\sin \beta -\cos \beta \Big )\frac{1}{\cosh \gamma } \\ y&= {\sqrt{2}}^\alpha \Big (\cos \beta +\sin \beta \Big )\frac{1}{\cosh \gamma } \\ z&= {\sqrt{2}}^{\alpha +1}\tanh \gamma \end{aligned}$$with \(\alpha ,\gamma \in \mathbb {R}\) and \(\beta \in [-\pi ,\pi )\).
-
(a)
Calculate the normalized and simplified ‘frame vectors’ \(\{\,\hat{\varvec{h}}_\alpha , \,\hat{\varvec{h}}_{\beta },\,\hat{\varvec{h}}_\gamma \}\).
-
(b)
Derive the gradient in this system.
-
(c)
Assume the vector field
$$\begin{aligned} \varvec{G}(\alpha ,\beta ,\gamma ) = \frac{\cosh \gamma }{ {\sqrt{2}}^{\alpha +1} \cos {\beta }}\, \,\hat{\varvec{h}}_\beta + \frac{\sinh \gamma }{{\sqrt{2}}^{\alpha +1} }\, \,\hat{\varvec{h}}_\gamma \end{aligned}$$to be conservative and determine the corresponding potential \(\Phi \).
-
(a)
Solutions
3.27. Work in a Non-Conservative Vector Field \(\varvec{F} = \Big ( \frac{1}{1+y^2},\quad -x \Big )^\top \)
a. Work for the Curve \(\varvec{\Psi } (t)= \Big ( \text {e}^{2t}-\text {e}^{t},\quad \text {e}^{t} \Big )^\top \)
We evaluate the vector field along the curve and multiply with the tangent vector
The work of moving a unit mass is found by the line integral
b. Non-Conservative Vector Field
In case of a conservative vector field, the following statements are equivalent:
-
1.
Each conservative vector field has a corresponding potential.
-
2.
The field is curl-free for every point in space.
-
3.
The work for moving a unit mass between two points is independent of the chosen path.
-
4.
For every closed curve, the work for moving a unit mass will vanish.
The given vector field is non-conservative if we can prove one of these conditions wrong. According to the question we should not use the curl, but we can calculate the work along different paths (Fig. 3.1).
An independent path is the straight line between the start point \(\varvec{A} = \begin{pmatrix} 0,&1 \end{pmatrix}^\top \) and the end point \(\varvec{B} = \begin{pmatrix} 12,&4 \end{pmatrix}^\top \):
As the work
differs from the previous results, this field is non-conservative.
3.28. Work Along the Curve \(\varvec{\Psi }(t) = \left( \frac{3t^2}{1+t^3},\quad \frac{3t}{1+t^3}\right) ^\top \) in the Force Field \(\varvec{F} = (-y,\quad x)^\top \)
We calculate the tangent vector
and evaluate the vector field along the curve
The work is determined by the line integral
-
The curve \(\varvec{\Psi }(t) = \begin{pmatrix} \frac{3t^2}{1+t^3},&\frac{3t}{1+t^3} \end{pmatrix}^\top \) is a parametric representation of the
 .
. -
This particular parametrization has a discontinuity in the origin \(\varvec{0}\), which is hidden in the double point of Fig. 3.2.
3.29. Work in a Non-Conservative Vector Field in Cylindrical Coordinates
To determine the curve, we use polar coordinates in the plane \(z=0\):
Hence, the projection of the cylinder onto the plane \(z = 0\) is represented by \(\rho = \sin \phi \) with \(\phi \in [0,\pi ]\). For the z-component we consider, that the curve is lying on the unit sphere:
Similar to the arc length we have to consider the modulus here. The effect of the modulus is shown by the black and the gray curve in Fig. 3.3b.
We split the curve into two parts
depending on the sign of the cosine-term.
In cylindrical coordinates, the tangent vectors are
We insert the curve into the vector field – expressed in cylindrical coordinates (cf. exercise 20) and consider \(\sqrt{\rho ^2+z^2} = r = 1\) and \(\lambda = \phi \):
To avoid mistakes with the modulus, we solve the two intervals separately. The first interval is limited by \(\phi \in \left[ 0,\frac{\pi }{2}\right] \) with the integrand:
and the work
Analogous, we calculate for the second interval \(\phi \in \left[ \frac{\pi }{2},\pi \right] \)
and
The total work is then the sum of its components:
-
Although the vector field is non-conservative (cf. exercise 19), the energy values in this closed curve and also in the two parts are zero. However, other closed curves with non-vanishing work must exist as well.
-
The intersection of a sphere and a cylinder – in the given geometrical relationship – leads to the so-called
 , also known as
, also known as  or
or  . The curve in this exercise consist in the upper part of this figure.
. The curve in this exercise consist in the upper part of this figure. -
Depending on the context, also the partial surface on the sphere might be called Viviani’s window (cf. Fig. 3.3).
3.30. Work in a Non-Conservative Field
The intersection of a plane and a circular cylinder leads to a conic section as well. In a geometrical parametrization, we would prove via eigen values that the intersection curve is an ellipse and determine dimension and rotation (Fig. 3.4).
In the algebraic method, we parametrize the cylinder with \(x = R \cos t\) and \(y = R\sin t\) and insert into the equation of the plane \(z = 1-\frac{R \cos t}{2}\) to derive the tangent vector:
Now we evaluate the vector field along curve and multiply with the tangent vector
We obtain the energy via the line integral
The work along this closed curve is depending on the radius R of the cylinder \(\mathcal {Z}\). By inserting \(R=1\), we find the work \(W = 0\), while for the radius \(R =2\) the work is equal to \(W = \pi 4\ln 2\).
3.31. Radial-Dependent Vector Field
-
Every radial-dependent vector field of the form \(\varvec{G} = f(r)\varvec{h}_r\) in spherical coordinates is conservative with the potential \(\Phi (r) = \int f(r) \mathrm {d}r \).
We recognize that the denominator is the derivative of the nominator:
The work of moving a unit mass is equal to the potential difference between start and end point of the curve, unless the curve is passing a singularity of the field. The given field has no singularity as the nominator has only complex or negative roots, while the spherical radius is positive.
The parameter \(t = 0 \) is equivalent to the point \(\varvec{A} = \varvec{\Psi }(0) = \begin{pmatrix} 0,&1,&0 \end{pmatrix}^\top \) with the radius \(r = 1\). Analogous, we obtain the point \(\varvec{\Psi }(\sqrt{\pi }) = \begin{pmatrix} \pi ,&-1,&\pi \end{pmatrix}^\top \) with the radius \(r = \sqrt{2\pi ^2+1}\) for the value \(t = \sqrt{\pi }\).
For computing the energy, we insert the 2 radii into the potential difference:
3.32. Finding a Potential in Cartesian Coordinates
To determine the coefficients, we derive the curl of the vector field:
The condition of a curl-free field leads to a set of linear equations for the unknowns. We solve the linear equations by the values \(\{a=1,b=1,c=-3,d=3\}\) and obtain a conservative vector field
a. Potential
First we integrate the gradient component \(\frac{\partial {\Phi }}{\partial {x}}\) via partial fraction decomposition
with a ‘constant’ depending on (y, z). Then we differentiate our result w.r.t. the coordinate y and compare with the gradient’s component:
We repeat the previous step for the z-component:
By combining we find the potential
corresponding to the vector field
3.33. Finding a Potential in Spherical Coordinates
For the potential, we compare the gradient (on the left) and the given vector field (on the right):
First we integrate the gradient component \(\frac{\partial {\Phi }}{\partial {r}}\)
with a ‘constant’ depending on \((\lambda ,\vartheta )\). Then we differentiate our result w.r.t. the coordinate \(\vartheta \) and compare with the gradient’s component:
We repeat the previous step for the \(\lambda \)-component:
By combining we find the potential
corresponding to the vector field
-
The order of integration and differentiation can be chosen freely. It is recommended to start with the simplest integral.
-
In this particular example, all three integrations are necessary to find the potential. In many cases, the potential is derived already after the first or second integration step.
3.34. Finding a Potential in Cylindrical Coordinates
a. Conservative Vector Field and its Potential
To find a conservative vector field, we investigate the curl:
To obtain a curl-free vector field with a potential \(\Phi \), we have to set \(\eta = -1\).
For the potential, we compare the gradient (on the left) and the given vector field (on the right):
First we integrate the gradient component \(\frac{\partial {\Phi }}{\partial {\rho }}\)
with a ‘constant’ depending on \((\phi , z)\). Then we differentiate our result w.r.t. the coordinate z and compare with the gradient’s component:
We repeat the previous step for the \(\phi \)-component:
By combining we find the potential
b. Work
The curve \(\varvec{\Psi } = 2\,\hat{\varvec{h}}_\rho +2\,\hat{\varvec{h}}_z\) is part of a circle in the plane \(\mathcal {E}: z = 2\) with radius \(\rho = 2\).
case 1: \(\eta = -1\)
In the case \(\eta = -1\), we find a conservative vector field with the corresponding potential \(\Phi = \sin \phi \ln |1|+\mathop {\mathrm {const.}}\nolimits \) and obtain the work \(W_{\eta = -1} = 0\) for all parts of the path.
case 1: \(\eta = 0\)
We evaluate the non-conservative field along the curve (with \(\rho = 2\) and \(z = 2\))
and insert it into the line integral with the tangent vector \(\varvec{T} = 2\,\hat{\varvec{h}}_\phi \):
For all intervals \(\phi _B = \phi _A+k\pi , k\in \mathbb {N}\) the energy will also vanish!
-
The work vanishes for the vector fields \(\varvec{G}_{\eta = 0}\) and \(\varvec{G}_{\eta = -1}\) for all closed circles \(\varvec{\Psi } = 2\,\hat{\varvec{h}}_\rho +2\,\hat{\varvec{h}}_z\).
-
In case of a conservative vector field with \(\eta = -1\), the work is always zero, when start and end point of the curve are lying on the cone \(\mathcal {C} :\Big \{\varvec{x}\in \mathbb {R}^3:\, x^2+y^2=z^2\Big \}\) due to the factor \(\ln \left| \frac{\cosh z}{\cosh \rho }\right| \) in the potential.
3.35. Finding a Potential in Parabolic Coordinates
a. ‘Frame Vectors’ and Gradient of Parabolic Coordinates
The ‘frame vectors’ have been derived in exercise 14 and we can directly write down the gradient
b. Potential
For the potential, we compare the gradient (on the left) and the given vector field (on the right):
First we integrate the gradient component \(\frac{\partial {\Phi }}{\partial {\gamma }}\)
with a ‘constant’ depending on \((\alpha ,\beta )\). Then we differentiate our result w.r.t. the coordinate \(\alpha \) and compare with the gradient’s component:
We repeat the previous step for the \(\beta \)-component:
By combining we find the potential
corresponding to the vector field
in the parabolic coordinate system.
3.36. Finding a Potential in Modified Spherical Coordinates
a. ‘Frame Vectors’ and Gradient
The ‘frame vectors’ have been derived in exercise 16. We insert them into the formula for the gradient:
b. Potential
For the potential, we compare the gradient (on the left) and the given vector field (on the right):
The corresponding potential has no terms of variable \(\alpha \), hence, only two integrations are necessary.
First we integrate the gradient component \(\frac{\partial {\Phi }}{\partial {\gamma }}\)
with a ‘constant’ depending on \((\alpha ,\beta )\). Then we differentiate our result w.r.t. the coordinate \(\beta \) and compare with the gradient’s component:
By combining we find the potential
-
In geosciences, the integral
$$\begin{aligned} \int \frac{1}{\cos {\beta }} \mathrm {d}\beta = \ln \left| \tan \left( \frac{\pi }{4}+\frac{\beta }{2}\right) \right| \end{aligned}$$is sometimes called
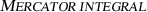 . The solution can be used to figure out isometric coordinates on the sphere or ellipsoid.
. The solution can be used to figure out isometric coordinates on the sphere or ellipsoid. -
The integral can be solved in many different ways, e.g. the substitution of Weierstraß, trigonometric identities, integration by parts or simply by expanding. The given solution is preferred for the isometric coordinates.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Antoni, M. (2019). Work, Line Integral and Potential. In: Calculus with Curvilinear Coordinates. Springer, Cham. https://doi.org/10.1007/978-3-030-00416-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-00416-3_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00415-6
Online ISBN: 978-3-030-00416-3
eBook Packages: EngineeringEngineering (R0)




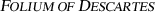 .
.
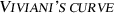 , also known as
, also known as 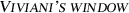 or
or  . The curve in this exercise consist in the upper part of this figure.
. The curve in this exercise consist in the upper part of this figure.
 . The solution can be used to figure out isometric coordinates on the sphere or ellipsoid.
. The solution can be used to figure out isometric coordinates on the sphere or ellipsoid.