Abstract
Dodis and Yu (TCC 2013) studied how the security of cryptographic primitives that are secure in the “ideal” model in which the distribution of a randomness is the uniform distribution, is degraded when the ideal distribution of a randomness is switched to a “real-world” (possibly biased) distribution that has some lowerbound on its min-entropy or collision-entropy. However, in many constructions, their security is guaranteed only when a randomness is sampled from some non-uniform distribution (such as Gaussian in lattice-based cryptography), in which case we cannot directly apply the results by Dodis and Yu.
In this paper, we generalize the results by Dodis and Yu using the Rényi divergence, and show how the security of a cryptographic primitive whose security is guaranteed when the ideal distribution of a randomness is a general (possibly non-uniform) distribution Q, is degraded when the distribution is switched to another (real-world) distribution R. More specifically, we derive two general inequalities regarding the Rényi divergence of R from Q and an adversary’s advantage against the security of a cryptographic primitive. As applications of our results, we show (1) an improved reduction for switching the distributions of distinguishing problems with public samplability, which is simpler and much tighter than the reduction by Bai et al. (ASIACRYPT 2015), and (2) how the differential privacy of a mechanism is degraded when its randomness comes from not an ideal distribution Q but a real-world distribution R. Finally, we show methods for approximate-sampling from an arbitrary distribution Q with some guaranteed upperbound on the Rényi divergence (of the distribution R of our sampling methods from Q).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In a non-cryptographic context, it is typical to define the \(\alpha \)-Rényi divergence as the logarithm of the quantity \(\mathtt {RD}_{\alpha }\) defined here [23].
- 2.
- 3.
We can also obtain the proof of the case \(\alpha = 2\) of our first lemma by setting \(c = 0\) in this proof. Setting other values for c does not seem to give us any merit.
- 4.
In [11], r was called a “secret key”. Since r can be any value sampled in the security game, we call it just a “parameter”.
- 5.
Resource of an adversary abstractly models all of an adversary’s efficiency measures, e.g. the running time, the circuit size, the number of oracle queries, etc.
- 6.
Note that for unpredictability applications, the absolute value of an adversary \(\mathsf {A}\)’s advantage can be removed.
- 7.
Note that the first bound does not involve the (non-square) advantage
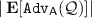 , and hence is true regardless of the (non-square) security of \(\varPi \) in the \(\mathcal {Q}\)-model.
, and hence is true regardless of the (non-square) security of \(\varPi \) in the \(\mathcal {Q}\)-model. - 8.
A failure predicate models the restrictions in a security game that typically prevent an adversary from winning the game trivially, e.g., submitting the challenge ciphertext as a decryption query in the IND-CCA security game of an encryption scheme.
- 9.
This is to offset an adversary’s advantage in case it violates the failure predicate F. How an adversary’s advantage is affected in case it violates the failure predicate F is not explicit in the definition of [11], and thus we adopt (seemingly) the most natural choice which is also convenient for our purpose.
- 10.
We stress that \(\mathsf {S}\) is not given as input the parameter r used to generate a sample x, but may instead infer whatever it needs to know from x for generating \(x'\).
- 11.
If we adopt the approach of Micciancio and Walter [18] that regards
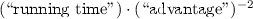 (which corresponds to the steps needed to solve a distinguishing problem with a constant advantage) of the best adversary as the “bit security” of a problem, the difference between our reduction and that of Bai et al. will be even larger.
(which corresponds to the steps needed to solve a distinguishing problem with a constant advantage) of the best adversary as the “bit security” of a problem, the difference between our reduction and that of Bai et al. will be even larger.
References
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange - a new hope. In: Proceedings of USENIX Security 2016, pp. 327–343. USENIX Association (2016)
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Bai, S., Langlois, A., Lepoint, T., Stehlé, D., Steinfeld, R.: Improved security proofs in lattice-based cryptography: using the Rényi divergence rather than the statistical distance. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 3–24. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_1
Barak, B., et al.: Leftover hash lemma, revisited. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 1–20. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_1
Barak, B., Shaltiel, R., Tromer, E.: True random number generators secure in a changing environment. In: Walter, C.D., Koç, Ç.K., Paar, C. (eds.) CHES 2003. LNCS, vol. 2779, pp. 166–180. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45238-6_14
Bogdanov, A., Guo, S., Masny, D., Richelson, S., Rosen, A.: On the hardness of learning with rounding over small modulus. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part I. LNCS, vol. 9562, pp. 209–224. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_9
Chaudhuri, K., Sarwate, A.D., Sinha, K.: Near-optimal differentially private principal components. In: Proceedings of NIPS 2012, pp. 998–1006 (2012)
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Dodis, Y., Ristenpart, T., Vadhan, S.: Randomness condensers for efficiently samplable, seed-dependent sources. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 618–635. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_35
Dodis, Y., Yao, Y.: Privacy with imperfect randomness. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 463–482. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_23
Dodis, Y., Yu, Y.: Overcoming weak expectations. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 1–22. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_1
Dwork, C.: Differential privacy. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006, Part II. LNCS, vol. 4052, pp. 1–12. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_1
Dwork, C., Kenthapadi, K., McSherry, F., Mironov, I., Naor, M.: Our data, ourselves: privacy via distributed noise generation. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 486–503. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_29
Dwork, C., McSherry, F., Nissim, K., Smith, A.: Calibrating noise to sensitivity in private data analysis. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 265–284. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_14
Gentry, C., Halevi, S.: Implementing Gentry’s fully-homomorphic encryption scheme. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 129–148. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_9
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of STOC 2008, pp. 197–206. ACM (2008)
Micciancio, D., Walter, M.: Gaussian sampling over the integers: efficient, generic, constant-time. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 455–485. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_16
Micciancio, D., Walter, M.: On the bit security of cryptographic primitives. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 3–28. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_1
Prest, T.: Sharper bounds in lattice-based cryptography using the Rényi divergence. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part I. LNCS, vol. 10624, pp. 347–374. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_13
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of STOC 2005, pp. 84–93. ACM (2005)
Rényi, A.: On measures of entropy and information. In: Proceedings of Fourth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 547–561. University of California Press (1961)
Takashima, K., Takayasu, A.: Tighter security for efficient lattice cryptography via the Rényi divergence of optimized orders. In: Au, M.-H., Miyaji, A. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 412–431. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26059-4_23
van Erven, E., Harremoës, P.: Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 60(7), 3797–3820 (2014)
Yao, Y., Li, Z.: Overcoming weak expectations via the Rényi entropy and the expanded computational entropy. In: Padró, C. (ed.) ICITS 2013. LNCS, vol. 8317, pp. 162–178. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04268-8_10
Acknowledgement
The authors would like to thank the anonymous reviewers of PKC 2019 for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Lemma 9
Let \(k \in \mathbb {N}\) and \(A = (a_1,\dots , a_k) \in (\mathbb {R}_{\ge 0})^k\) such that \(\sum _{i \in [k]} a_i \in \mathbb {N}\). For each \(i \in [k]\), let \(\delta _i := \lceil a_i \rceil - a_i\). Also, define
Note that since \(\sum _{i \in [k]} a_i \in \mathbb {N}\) and \(\delta _i \in [0,1)\) for every \(i \in [k]\), the definition of \(\varDelta \) implies \(\varDelta \in \mathbb {Z}_{\ge 0}\) and \(\varDelta < k\). Furthermore, let \(\mathcal {S}_{\mathtt {up}}\) and \(\mathcal {S}_{\mathtt {low}}\) be subsets of [k] satisfying the following four conditions:
-
(1) \(\mathcal {S}_{\mathtt {up}}\cup \mathcal {S}_{\mathtt {low}}= [k]\)
-
(2) \(\mathcal {S}_{\mathtt {up}}\cap \mathcal {S}_{\mathtt {low}}= \emptyset \)
-
(3) \(|\mathcal {S}_{\mathtt {up}}| = \varDelta \)
-
(4) \(\max \{\delta _i | i \in \mathcal {S}_{\mathtt {low}}\} \le \min \{\delta _i|i \in \mathcal {S}_{\mathtt {up}}\}\).
Using them, define the vector \(B = (b_1,\dots , b_k)\) such that for every \(i \in [k]\),
By definition, every \(b_i\) is an integer. Since \(a_i \in \mathbb {R}_{\ge 0}\) for every \(i \in [k]\), we have \(b_i \in \mathbb {Z}_{\ge 0}\) for every \(i \in \mathcal {S}_{\mathtt {low}}\). Note also that by the definitions of \(\varDelta \) and \(\mathcal {S}_{\mathtt {up}}\), we have \(|\{i \in [k]| \delta _i > 0\}| \ge \varDelta = |\mathcal {S}_{\mathtt {up}}|\), and thus \(a_i > 0\) holds for every \(i \in \mathcal {S}_{\mathtt {up}}\), which implies \(b_i = \lceil a_i \rceil - 1 \ge 0\) for every \(i \in \mathcal {S}_{\mathtt {up}}\). Hence, we have \(B = (b_1,\dots , b_k) \in (\mathbb {Z}_{\ge 0})^k\).
In the following we confirm that the vector B defined above satisfies both of the properties. Regarding the first property, we have
where the equality (*) uses \(|\mathcal {S}_{\mathtt {up}}| = \varDelta \). Hence, B satisfies the first property.
It remains to show that B satisfies the second property. For each \(i \in [k]\), let
Recall that \(\delta _i \in [0,1)\) holds for every \(i \in [k]\). Thus, we have \(|d_i| \le 1\) for all \(i \in [k]\). Furthermore, for every \((i,j) \in [k]^2\), we have
From the above, it is immediate that \(|d_i - d_j| \le 1\) holds for the cases \((i,j) \in (\mathcal {S}_{\mathtt {low}})^2\) and \((i,j) \in (\mathcal {S}_{\mathtt {up}})^2\). Also, for the case \((i, j) \in \mathcal {S}_{\mathtt {low}}\times \mathcal {S}_{\mathtt {up}}\), we have \(\delta _i \le \delta _j\) due to the condition (4) of \(\mathcal {S}_{\mathtt {low}}\) and \(\mathcal {S}_{\mathtt {up}}\), and thus we have \(|1-(\delta _j - \delta _i)| \le 1\). Similarly, for the case \((i, j) \in \mathcal {S}_{\mathtt {up}}\times \mathcal {S}_{\mathtt {low}}\), we have \(\delta _i \ge \delta _j\), and thus we have \(|\delta _i - \delta _j - 1| \le 1\). Hence, we have \(|d_i - d_j| \le 1\) for any pair \((i,j) \in [k]^2\). This shows that the vector B satisfies the second property as well. \(\square \) (Lemma 9)
B Proof of Lemma 11
Fix arbitrarily a number \(k \in \mathbb {N}\) and a vector \((a_1,\dots ,a_n) \in \mathbb {R}^k\) satisfying \(|a_i - a_j| \le 1\) for all \(i,j \in [k]\), and let \(\alpha := \sum _{i \in [k]} a_i\). We will show that \(\sum _{i \in [k]} a_i^2 \le \frac{\alpha ^2}{k} + \frac{k}{4}\) holds, which proves the lemma.
Let \(a_{\min }:= \min \{a_i\}_{i \in [k]}\), and \(\delta _i := a_i - a_{\min }\) for each \(i \in [k]\). Note that due to the given condition of the vector \((a_1,\dots ,a_k)\), \(\delta _i \in [0,1]\) holds for all \(i \in [k]\). We also have
Furthermore, for each \(i \in [k]\), we have
where the inequality uses \(\delta _i^2 \le \delta _i\), which is due to \(\delta _i \in [0,1]\).
Now, consider the sum of squares \(\sum _{i \in [k]} a_i^2\). We have
where the inequality (*) uses Eq. (19), and the equality (†) uses Eq. (18).
\(\square \) (Lemma 11)
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Matsuda, T., Takahashi, K., Murakami, T., Hanaoka, G. (2019). Improved Security Evaluation Techniques for Imperfect Randomness from Arbitrary Distributions. In: Lin, D., Sako, K. (eds) Public-Key Cryptography – PKC 2019. PKC 2019. Lecture Notes in Computer Science(), vol 11442. Springer, Cham. https://doi.org/10.1007/978-3-030-17253-4_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-17253-4_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17252-7
Online ISBN: 978-3-030-17253-4
eBook Packages: Computer ScienceComputer Science (R0)


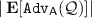 , and hence is true regardless of the (non-square) security of
, and hence is true regardless of the (non-square) security of 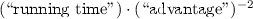 (which corresponds to the steps needed to solve a distinguishing problem with a constant advantage) of the best adversary as the “bit security” of a problem, the difference between our reduction and that of Bai et al. will be even larger.
(which corresponds to the steps needed to solve a distinguishing problem with a constant advantage) of the best adversary as the “bit security” of a problem, the difference between our reduction and that of Bai et al. will be even larger.