Abstract
This note is meant to introduce the reader to a duality principle for nonlinear equations recently discovered in Valtorta (Reverse Khas’minskii condition. Math Z 270(1):65–177, 2011), Mari and Valtorta (Trans Am Math Soc 365(9):4699–4727, 2013), and Mari and Pessoa (Commun Anal Geom, to appear). Motivations come from the desire to give a unifying potential-theoretic framework for various maximum principles at infinity appearing in the literature (Ekeland, Omori-Yau, Pigola-Rigoli-Setti), as well as to describe their interplay with properties coming from stochastic analysis on manifolds. The duality involves an appropriate version of these principles formulated for viscosity subsolutions of fully nonlinear inequalities, called the Ahlfors property, and the existence of suitable exhaustion functions called Khas’minskii potentials. Applications, also involving the geometry of submanifolds, will be discussed in the last sections. We conclude by investigating the stability of these maximum principles when we remove polar sets.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Here, as usual, if we write “w(x) → +∞ as x diverges” we mean that the sublevels of w have compact closure in X, that is, that w is an exhaustion.
- 2.
The radial sectional curvature is the sectional curvature restricted to 2-planes containing ∇ϱ. Inequality \(\mathrm {Sect}_{\mathrm {rad}} \geqslant - \mathrm {G}^2(\varrho )\) means that \(\mathrm {Sect}(\uppi _{\mathrm {x}}) \geqslant - \mathrm {G}^2\big (\varrho (\mathrm {x})\big )\) for each x∉{o}∪cut(o) and \(\uppi _{\mathrm {x}} \leqslant \mathrm {T}_{\mathrm {x}} \mathrm {X}\) 2-plane containing ∇ρ.
- 3.
That is, the opposite of the roots of
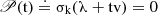 .
. - 4.
In [48], the uniform continuity of the Pucci operators in \((\mathcal {E} 6)\) is not explicitly stated but can be easily checked. For instance, in the case of \(\mathcal {P}^+_{\uplambda ,\Lambda }\), referring to Definition 2.23 in [48] and using the min-max definition,
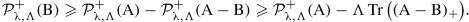
If ∥(A −B)+∥ < δ, then \(\mathcal {P}^+_{\uplambda ,\Lambda }(\mathrm {B}) \geqslant \mathcal {P}^+_{\uplambda ,\Lambda }(\mathrm {A}) - \mathrm {m}\Lambda \updelta \), that proves the uniform continuity of \(\mathrm {F}_{\uplambda ,\Lambda }^+\). The case of \(\mathrm {F}_{\uplambda , \Lambda }^-\) is analogous.
- 5.
Theorem 3.11 can be stated for F locally jet-equivalent to a universal example, provided that the strong maximum principle in \((\mathcal {H} 1')\) holds for each manifold Y and each \(\widetilde {\mathrm {F}} \subset \mathrm {J}^2(Y)\) constructed by gluing as in the theorem.
- 6.
By definition, a function u is semiconcave if and only if, locally, there exists v ∈C2, such that u + v is concave when restricted to geodesics.
References
L.V. Ahlfors, An extension of Schwarz’s lemma. Trans. Am. Math. Soc. 43, 359–364 (1938)
L.V. Ahlfors, L. Sario, Riemann Surfaces. Princeton Mathematical Series, vol. 26 (Princeton University Press, Princeton, 1960)
L.J. Alías, G.P. Bessa, M. Dajczer, The mean curvature of cylindrically bounded submanifolds. Math. Ann. 345(2), 367–376 (2009)
L.J. Alías, P. Mastrolia, M. Rigoli, Maximum Principles and Geometric Applications. Springer Monographs in Mathematics (Springer, Cham, 2016), xvii+570 pp.
L.J. Alías, J. Miranda, M. Rigoli, A new open form of the weak maximum principle and geometric applications. Commun. Anal. Geom. 24(1), 1–43 (2016)
G. Aronsson, Extension of functions satisfying Lipschitz conditions. Ark. Mat. 6, 551–561 (1967)
C. Bär, F. Pfäffle, Wiener measures on Riemannian manifolds and the Feynman-Kac formula. Mat. Contemp. 40, 37–90 (2011)
M. Bardi, F. Da Lio, On the strong maximum principle for fully nonlinear degenerate elliptic equations. Arch. Math. (Basel) 73, 276–285 (1999)
G.P. Bessa, B.P. Lima, L.F. Pessoa, Curvature estimates for properly immersed ϕh-bounded submanifolds. Ann. Mat. Pura Appl. 194(1), 109–130 (2015)
B. Bianchini, L. Mari, P. Pucci, M. Rigoli, On the interplay among maximum principles, compact support principles and Keller-Osserman conditions on manifolds (2018). Available at arXiv:1801.02102
A. Borbely, A remark on the Omori-Yau maximum principle. Kuwait J. Sci. Eng. 39(2A), 45–56 (2012)
A. Borbely, Stochastic completeness and the Omori-Yau maximum principle. J. Geom. Anal. (2017). https://doi.org/10.1007/s12220-017-9802-7
L. Caffarelli, X. Cabre, Fully Nonlinear Elliptic Equations. Colloquium Publications, vol. 43 (American Mathematical Society, Providence, 1995)
S.Y. Cheng, S.T. Yau, Differential equations on Riemannian manifolds and their geometric applications. Commun. Pure Appl. Math. 28(3), 333–354 (1975)
S.Y. Cheng, S.T. Yau, Maximal space-like hypersurfaces in the Lorentz-Minkowski spaces. Ann. Math. (2) 104(3), 407–419 (1976)
P. Collin, R. Kusner, W.H. Meeks III, H. Rosenberg, The topology, geometry and conformal structure of properly embedded minimal surfaces. J. Differ. Geom. 67(2), 377–393 (2004)
M.G. Crandall, A visit with the ∞-Laplace equation, in Calculus of Variations and Nonlinear Partial Differential Equations. Lecture Notes in Mathematics, vol. 1927 (Springer, Berlin, 2008), pp. 75–122
M.G. Crandall, H. Ishii, P.L. Lions, User’s guide to viscosity solutions of second-order partial differential equations. Bull. Am. Math. Soc. 27, 1–67 (1992)
M.G. Crandall, L.C. Evans, R.F. Gariepy, Optimal Lipschitz extensions and the infinity Laplacian. Calc. Var. P.D.E. 13(2), 123–139 (2001)
M.P. Do Carmo, Riemannian Geometry. Mathematics: Theory and Applications (Birkäuser Boston Inc., Boston, 1992)
J. Dodziuk, Maximum principle for parabolic inequalities and the heat flow on open manifolds. Indiana Univ. Math. J. 32(5), 703–716 (1983)
D.M. Duc, J. Eells, Regularity of exponentially harmonic functions. Int. J. Math. 2, 395–408 (1991)
I. Ekeland, On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974)
M. Emery, Stochastic Calculus in Manifolds. Universitext (Springer, Berlin, 1989)
F. Fontenele, F. Xavier, Good shadows, dynamics and convex hulls of complete submanifolds. Asian J. Math. 15(1), 9–31 (2011)
L. Gärding, An inequality for hyperbolic polynomials. J. Math. Mech. 8, 957–965 (1959)
R.E. Greene, H. Wu, C∞ approximation of convex, subharmonic, and plurisubharmonic functions. Ann. Sci. Ec. Norm. Sup. 4e serie t.12, 47–84 (1979)
A. Grigor’yan, Analytic and geometric background of recurrence and non-explosion of the Brownian motion on Riemannian manifolds. Bull. Am. Math. Soc. 36, 135–249 (1999)
F.R. Harvey, H.B. Lawson Jr., Dirichlet duality and the non-linear Dirichlet problem. Commun. Pure Appl. Math. 62, 396–443 (2009)
F.R. Harvey, H.B. Lawson Jr., Dirichlet duality and the nonlinear Dirichlet problem on Riemannian manifolds. J. Differ. Geom. 88, 395–482 (2011)
F.R. Harvey, H.B. Lawson Jr., Geometric plurisubharmonicity and convexity: an introduction. Adv. Math. 230(4–6), 2428–2456 (2012)
F.R. Harvey, H.B. Lawson Jr., Existence, uniqueness and removable singularities for nonlinear partial differential equations in geometry, in Surveys in Differential Geometry 2013, vol. 18, ed. by H.D. Cao, S.T. Yau (International Press, Somerville, 2013), pp. 102–156
F.R. Harvey, H.B. Lawson Jr., Gärding’s theory of hyperbolic polynomials. Commun. Pure Appl. Math. 66(7), 1102–1128 (2013)
F.R. Harvey, H.B. Lawson Jr., Removable singularities for nonlinear subequations. Indiana Univ. Math. J. 63(5), 1525–1552 (2014)
F.R. Harvey, H.B. Lawson Jr., Characterizing the strong maximum principle for constant coefficient subequations. Rend. Mat. Appl. (7) 37(1–2), 63–104 (2016)
I. Holopainen, Nonlinear potential theory and quasiregular mappings on Riemannian manifolds. Ann. Acad. Sci. Fenn. Ser. A I Math. Dissertationes 74, 45 pp. (1990)
D. Impera, S. Pigola, A.G. Setti, Potential theory for manifolds with boundary and applications to controlled mean curvature graphs. J. Reine Angew. Math. 733, 121–159 (2017)
R. Jensen, Uniqueness of Lipschitz extensions: minimizing the sup norm of the gradient. Arch. Ration. Mech. Anal. 123(1), 51–74 (1993)
P. Juutinen, Absolutely minimizing Lipschitz extensions on a metric space. Ann. Acad. Sci. Fenn. Math. 27(1), 57–67 (2002)
L. Karp, Differential inequalities on complete Riemannian manifolds and applications. Math. Ann. 272(4), 449–459 (1985)
B. Kawohl, N. Kutev, Strong maximum principle for semicontinuous viscosity solutions of nonlinear partial differential equations. Arch. Math. (Basel) 70(6), 470–478 (1998)
R.Z. Khas’minskii, Ergodic properties of recurrent diffusion processes and stabilization of the solution of the Cauchy problem for parabolic equations. Teor. Verojatnost. i Primenen., Akademija Nauk SSSR. Teorija Verojatnosteı̆ i ee Primenenija 5, 196–214 (1960)
N.V. Krylov, On the general notion of fully nonlinear second-order elliptic equations. Trans. Am. Math. Soc. 347(3), 857–895 (1995)
Z. Kuramochi, Mass distribution on the ideal boundaries of abstract Riemann surfaces I. Osaka Math. J. 8, 119–137 (1956)
P. Li, Harmonic functions and applications to complete manifolds. XIV Escola de Geometria Diferencial: Em homenagem a Shiing-Shen Chern (2006)
P. Li, L.-F. Tam, Harmonic functions and the structure of complete manifolds. J. Differ. Geom. 35, 359–383 (1992)
M. Magliaro, L. Mari, M. Rigoli, On a paper of Berestycki-Hamel-Rossi and its relations to the weak maximum principle at infinity, with applications. Rev. Mat. Iberoam. 34, 915–936 (2018)
L. Mari, L.F. Pessoa, Duality between Ahlfors-Liouville and Khas’minskii properties for non-linear equations. Commun. Anal. Geom. (to appear)
L. Mari, M. Rigoli, Maps from Riemannian manifolds into non-degenerate Euclidean cones. Rev. Mat. Iberoam. 26(3), 1057–1074 (2010)
L. Mari, D. Valtorta, On the equivalence of stochastic completeness, Liouville and Khas’minskii condition in linear and nonlinear setting. Trans. Am. Math. Soc. 365(9), 4699–4727 (2013)
L. Mazet, A general halfspace theorem for constant mean curvature surfaces. Am. J. Math. 135(3), 801–834 (2013)
W.H. Meeks III, H. Rosenberg, Maximum principles at infinity. J. Differ. Geom. 79(1), 141–165 (2008)
M. Nakai, On Evans potential. Proc. Jpn. Acad. 38, 624–629 (1962)
M. Nakai, L. Sario, Classification Theory of Riemann Surfaces (Springer, Berlin, 1970)
H. Omori, Isometric immersions of Riemannian manifolds. J. Math. Soc. Jpn. 19, 205–214 (1967)
S. Pigola, A.G. Setti, Global Divergence Theorems in Nonlinear PDEs and Geometry. Ensaios Matemáticos [Mathematical Surveys], vol. 26 (Sociedade Brasileira de Matemática, Rio de Janeiro, 2014), ii+77 pp.
S. Pigola, M. Rigoli, A.G. Setti, A remark on the maximum principle and stochastic completeness. Proc. Am. Math. Soc. 131(4), 1283–1288 (2003)
S. Pigola, M. Rigoli, A.G. Setti, Maximum principles on Riemannian manifolds and applications. Mem. Am. Math. Soc. 174(822) (2005)
S. Pigola, M. Rigoli, A.G. Setti, Some non-linear function theoretic properties of Riemannian manifolds. Rev. Mat. Iberoam. 22(3), 801–831 (2006)
S. Pigola, M. Rigoli, A.G. Setti, Maximum principles at infinity on Riemannian manifolds: an overview. Mat. Contemp. 31, 81–128 (2006). Workshop on Differential Geometry (Portuguese)
S. Pigola, M. Rigoli, A.G. Setti, Vanishing and Finiteness Results in Geometric Analysis. A Generalization of the Böchner Technique. Progress in Mathematics, vol. 266 (Birkäuser, Boston, 2008)
S. Pigola, M. Rigoli, A.G. Setti, Aspects of potential theory on manifolds, linear and non-linear. Milan J. Math. 76, 229–256 (2008)
P. Pucci, J. Serrin, The Maximum Principle. Progress in Nonlinear Differential Equations and Their Applications, vol. 73 (Birkhäuser Verlag, Basel, 2007), p. x+235
P. Pucci, M. Rigoli, J. Serrin, Qualitative properties for solutions of singular elliptic inequalities on complete manifolds. J. Differ. Equ. 234(2), 507–543 (2007)
J.P. Sha, p-Convex riemannian manifolds. Invent. Math. 83, 437–447 (1986)
D.W. Stroock, S.R.S. Varadhan, Multidimensional Diffusion Processes. Reprint of the 1997 edition. Classics in Mathematics (Springer, Berlin, 2006), xii+338 pp.
F. Sullivan, A characterization of complete metric spaces. Proc. Am. Math. Soc. 83(2), 345–346 (1981)
C.-J. Sung, L.-F. Tam, J. Wang, Spaces of harmonic functions. J. Lond. Math. Soc. 61(3), 789–806 (2000)
M. Troyanov, Parabolicity of manifolds. Sib. Adv. Math. 9(4), 125–150 (1999)
D. Valtorta, Potenziali di Evans su varietá paraboliche (2009). Available at arXiv:1101.2618
D. Valtorta, Reverse Khas’minskii condition. Math. Z. 270(1), 65–177 (2011)
J.D. Weston, A characterization of metric completeness. Proc. Am. Math. Soc. 64(1), 186–188 (1977)
H. Wu, Manifolds of partially positive curvature. Indiana Univ. Math. J. 36(3), 525–548 (1987)
S.T. Yau, Harmonic functions on complete Riemannian manifolds. Commun. Pure Appl. Math. 28, 201–228 (1975)
S.T. Yau, A general Schwarz lemma for Kähler manifolds. Am. J. Math. 100(1), 197–203 (1978)
Acknowledgements
This work was completed when the second author was visiting the Abdus Salam International Center for Theoretical Physics (ICTP), Italy. He is grateful for the warm hospitality and for financial support. The authors would also like to thank the organizing and local committees of the INdAM workshop “Contemporary Research in elliptic PDEs and related topics” (Bari, May 30/31, 2017) for the friendly and pleasant environment.
The first author “Luciano Mari” is supported by the grants SNS17_B_MARI and SNS_RB_MARI of the Scuola Normale Superiore.
The second author “Leandro F. Pessoa” was partially supported by CNPq-Brazil.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Mari, L., Pessoa, L.F. (2019). Maximum Principles at Infinity and the Ahlfors-Khas’minskii Duality: An Overview. In: Dipierro, S. (eds) Contemporary Research in Elliptic PDEs and Related Topics. Springer INdAM Series, vol 33. Springer, Cham. https://doi.org/10.1007/978-3-030-18921-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-18921-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18920-4
Online ISBN: 978-3-030-18921-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


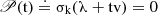 .
.