Flow and Heat Transfer in Porous Media

Abstract

This chapter considers single-and multiphase heat and mass transfer in porous media as well as boiling, condensation, melting and solidification in porous media.

Problems

• 12.1. A capillary porous structure with partial heating and evaporation on its upper surface is shown in Fig. P12.1. The entire porous structure is saturated with liquid from the bottom surface (y = 0), which is connected to a pool for liquid supply. A constant heat flux, $q_{0}^{\prime \prime }$, is applied over part of the upper surface (0 < x < L_xf), which is impermeable to the fluid. The rest of the upper surface (L_xf < x < L_x) exposes liquid in the pores of the capillary structure to the vapor space above. Heat is transferred from the left portion of the upper surface to the right portion of the upper surface, where evaporation takes place. The left and right sidewalls are adiabatic and impermeable. At steady state, the liquid is drawn from the bottom of the porous structure and flows to the right portion of the upper surface due to evaporation. If the liquid velocity at the bottom surface and the vapor velocity at the upper surface are uniform, determine the liquid velocity at the bottom, $v_{\ell }$, and the vapor velocity at the upper surface, $v_{\text{v}}$.

  

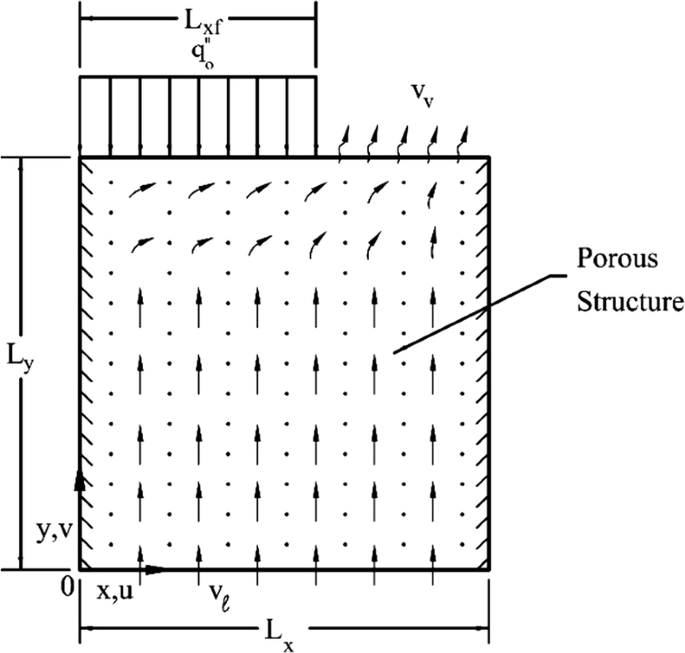
  Fig. P12.1

• 12.2. The area-averaged velocity components in the x- and y-directions in Problem 12.1 can be estimated by Darcy’s law:

  $$u = - \frac{K}{\mu }\frac{\partial p}{\partial x} \, v = - \frac{K}{\mu }\frac{\partial p}{\partial y}$$

  where K is permeability. The continuity equation is

  $$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

  Determine the analytical solution for the pressure and velocity distributions in the porous structure.

• 12.3. Specify the energy equation and the corresponding boundary conditions for Problem 12.2; then nondimensionalize them. Write a computer program to obtain dimensionless temperature distribution in the porous media.

• 12.4. For a porous bed made of spherical balls packed in a body-centered cubic (BCC) formation, use the continuity Eq. (3.51) and momentum Eqs. (3.72)–(3.74), to develop the boundary conditions and numerically solve the flow field, and determine the permeability of the packed bed by plotting the product of μv versus dp/dx. Assume that the elemental cube’s sides all have a length of 10⁻³ m and that the spheres all have a radius of 4.6 × 10⁻⁴ m. (Note: the spheres are slightly compressed against each other, and therefore, their radii are slightly larger than if they were only contacting one another at a single point). Model the top right quadrant of an elementary cubic cell, Fig. P12.4. Numerically solve the problem for different fluids and determine the permeability.

  

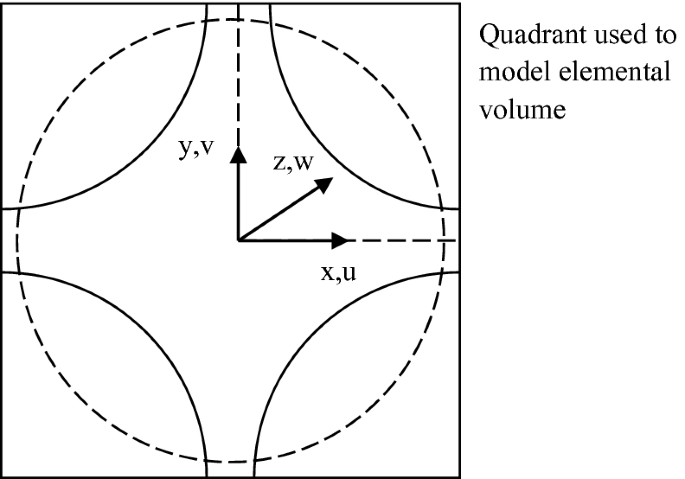
  Fig. P12.4

• 12.5. For most heat pipes, the wick structures are very thin, so the liquid flow in the wick can be simplified to one-dimensional axial flow. Since the liquid velocity and its gradient in the axial direction are very small, the liquid flow in the wick satisfies Darcy’s law, i.e., $w_{\ell } = - \frac{K}{{\mu_{\ell } }}\frac{{{\text{d}}{\text{p}}_{\ell } }}{{{\text{d}}z}}$, where K is permeability. For an axially grooved wick structure as shown in Fig. P12.5, determine the permeability analytically.

  

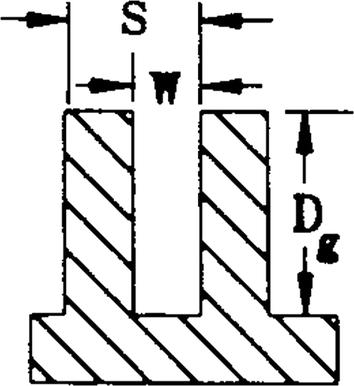
  Fig. P12.5

• 12.6. The designer of a coffee maker wants to make a filtration system in which the water is heated and filtered at the same time. The filter can be modeled as a porous zone within a tube, and the heat can be modeled as a uniform heat flux applied to the tube’s outer wall. Set up the governing equations and boundary conditions so that the designer can get a temperature and pressure field, and thus know when the liquid may start to boil.

• 12.7. A conventional heat pipe with multiple heat sources, as shown in Fig. P12.7, is divided into three regions: vapor-flow region, liquid–wick region, and solid wall. The effect of gravity can be neglected so that the fluid flow and heat transfer can be treated as two-dimensional. Develop conservation governing equations and corresponding boundary conditions for all three regions. Furthermore, develop interfacial mass and energy balance between regions.

  

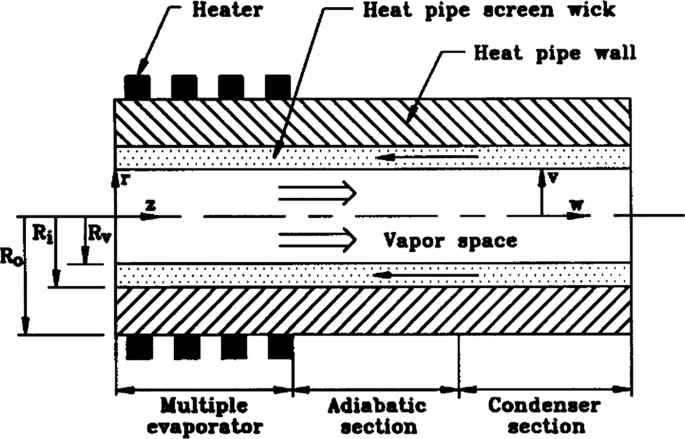
  Fig. P12.7

• 12.8. The boundary of a porous zone is subjected to a constant heat flux. The porous zone is in local thermal nonequilibrium. Specify the thermal boundary conditions for the fluid phase and the thermal boundary condition for the solid phase. Also discuss the physical significance of your boundary conditions.

• 12.9. Consider the direct–methanol fuel cell (DMFC) with a liquid feed presented in Fig. P12.9. Assume that the methanol solution is passing over the fuel cell at a very high velocity, and that solution has a constant concentration at the top of the anode gas diffusion layer. The oxygen supplied to the cathode comes from air. Assume that the catalyst layers are very thin; therefore, their thickness can be neglected and the reaction rates can be considered to be a surface reaction rate. The membrane can be considered saturated at all times. Develop the governing equations and boundary conditions for the transport of liquid and gas through the fuel cell as well as the electric potentials of the membrane and gas diffusion layers for a one-dimensional steady-state simulation.

  

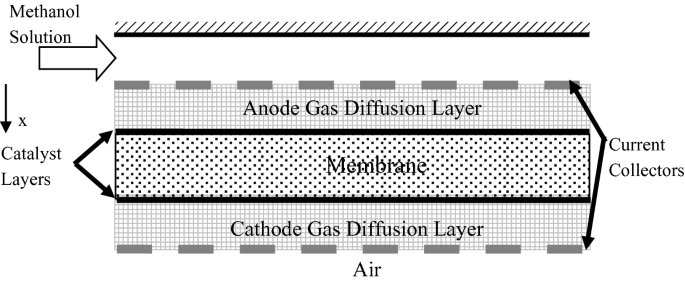
  Fig. P12.9

• 12.10. The multiphase transport model in porous media can also be used to model two-phase flow in microchannel heat exchangers. The transport phenomena in a microchannel heat exchanger can be characterized as unidirectional flow combined with three-dimensional conduction. Set up the governing equations for this system, while leaving the terms caused by phase interaction and solid–fluid interaction unclosed. The energy equation shall be written in terms of internal energy, and the solid, liquid, and vapor equations shall be set up separately.

• 12.11. In a fluidized bed, particles are supported by an upward flow of fluid around them as shown in Fig. P12.11. Formulate the problem as multifluid model and deduce the fluid flux and pressure gradient needed to cause fluidization in a bed with void fraction ε_f by neglecting inertia. Assume one-dimensional, incompressible, steady flow with negligible interparticle forces and no phase change.

  

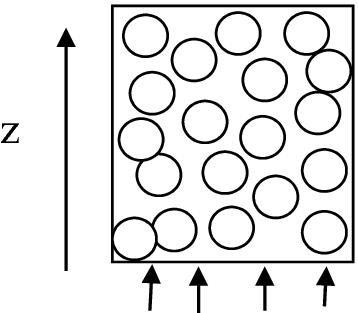
  Fig. P12.11

• 12.12. A horizontal elliptical tube with a major axis 2a and minor axis 2b is embedded in a porous medium filled with a dry saturated vapor, as shown in Fig. P12.12. A dry saturated vapor flows downward with uniform vertical velocity U_∞. Since the temperature of the elliptical tube, T_w, is below the saturation temperature of the vapor, T_sat, condensation takes place at the surface of the elliptical tube. Specify the governing equation and corresponding boundary conditions for this problem.

  

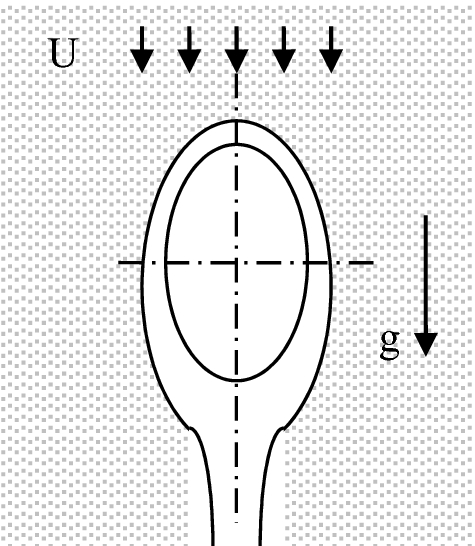
  Fig. P12.12

• 12.13. Gas-loaded heat pipes have been applied in many diverse fields and are useful when the temperature of a device must be held constant while a variable heat load is dissipated. The physical configuration and coordinate system of a gas-loaded heat pipe are shown in Fig. P12.13. Develop the appropriate conservation equations for transient, compressible, two-species flow for mass, momentum, energy, and species in vapor space, wick, and wall including initial and boundary condition for a two-dimensional transient gas-loaded heat pipe.

  

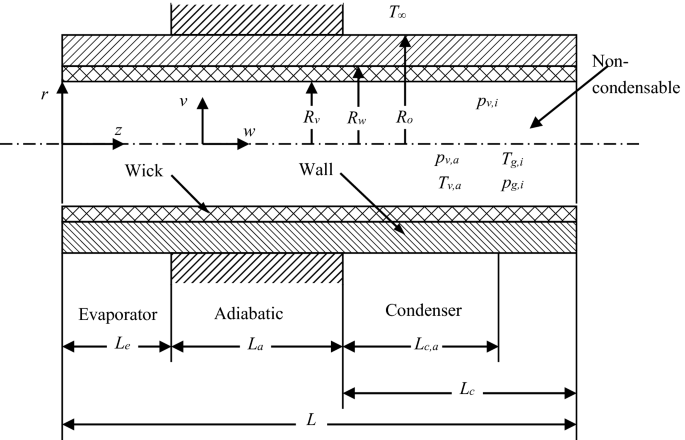
  Fig. P12.13