Keywords

1 Introduction

There is a problem with computers in schools. Schools can rarely guarantee every student access to a computer, so the curriculum is largely designed without assuming this equipment will be available. Yet outside school, students, citizens and professionals use digital technologies intensively. This study aimed to reconcile this incongruity, and to counter diminishing learning achievements in Australian schools.

School curricula change very slowly. They are not controlled by content experts, but by communities, politicians, educators and others. Therefore, new knowledge can take time to be adopted. In 2005, we celebrated the centenary of Einstein’s special theory of relativity [1], but this is rarely found in primary schools. Technology and science continue to advance rapidly [2], often outstripping community discussion and legal controls. Disparities between the school curriculum and the lived world of children embedded in artefacts created from recent knowledge can lead to tension for them and their teachers. One way to bring new knowledge into schools may be to use computers. However, even computers are not making the desired impact in education. An OECD report [3] showed a weak inverse relationship between computer investments in schools and student achievement in the Programme for International Student Assessment (PISA). This is, therefore, a wicked problem in education. When students regularly use computers to create text using keyboards, they are unlikely to develop the handwriting skills demanded in the current curriculum. So, these findings are not entirely unexpected. But how can learning achievements be improved and new skills and ideas enter the curriculum? A transformative perspective is necessary, looking beyond the current curriculum to new skills and higher order thinking [4]. These authors initially saw transformation as “an integral component of broader curricular reforms that change not only how students learn but also what they learn” and went on to suggest it could become “an integral component of the reforms that alter the organisation and structure of schooling itself” (ibid, p. 2).

It is suggested that new theoretical approaches are needed to compare transformative uses of computers in schools. Puentedura’s Substitution, Augmentation, Modification, and Redefinition (SAMR) model [5] provides a framework for thinking about transforming school curricula with computers, but there is still neither a clear way of defining transformation, nor of measuring it. In this study, we tried using computers to change what students learnt in a very specific way. Material within the school mathematics subject is structured in a similar way across many jurisdictions. In particular, we could not find evidence of integral calculus being taught in primary school (up to age 12 years) in any widespread fashion. Therefore, the Calculus for Kids project used computers to teach this topic to both younger and older students. This article looks at the similarities and differences between the two groups.

2 Previous Work

Before explaining how this project could solve these entwined wicked problems, it is important to have an accepted way to measure the impact of an educational innovation. Meta-studies such as that by Hattie and Yates [6] have established ‘effect size’ (often using the statistical measure of Cohen’s d) as a measure of innovation impact on learning achievement. A hinge point effect size of 0.4 has been identified as the minimum for a significant innovation [7]. Studies have shown that “supplementing traditional teaching… computers were particularly effective when used to extend study time and practice, when used to allow students to assume control over the learning situation… and when used to support collaborative learning” [3]. In these meta-studies, computer aided instruction was found to have an intervention effect size of 0.55 to 0.57.

When assessing the learning of any group of students, their achievements generally lie on a normal curve: a few do well; some under-perform; and most perform close to the average. After a group of students receives a successful teaching intervention, the group demonstrates higher achievement, so the distribution curve of achievement moves to the right. The quantum of the improvement is crucial to determining the effectiveness of the intervention. An effect size of 1.0 corresponds to an improvement of one standard deviation. Glass et al. [8] indicated that normal learning progress is about one standard deviation per year.

The Calculus for Kids intervention taught both Year 6 (aged 12 years) and Year 9 (aged 15 years) students to solve real-world problems using integral calculus with computer algebra software. This achieved a published intervention effect size between 1.85 and 25.53 [9] for the Year 6 students. The effect size of this transformative intervention was over four times the size of Hattie’s hinge point (0.4) for a significant intervention [7]. The nearest other high effect size for new ways of using computers in class was reported by Puentedura [10] with ‘redefinition’ types of computer uses providing effect sizes of 1.6.

David Perkins provided the concept of ‘person-plus’ to embody the shared cognition of a learner assisted by their notebook [11]. In our project, we acknowledge this notebook could be a notebook computer, or any kind of specialised electronic assistive device. This ‘person-plus’ view supports arguments for open book assessment, because it is closer to real-world problem solving. The assistive device improves information retrieval and accuracy, and Perkins argues this leads to higher order knowledge. By extension, a student using modern digital technology can solve problems that are more complex. This models human adoption of other mind tools such as language, numbering systems and so on. Moursund’s extension [12] divided problems into three groups: those which are more readily solved by humans alone; those best solved by computers alone; and those which are best solved by humans working in combination with computers. This project probed the transformative effects of students learning in partnership with their computers.

Computational thinking was popularised by Jeannette Wing [13] and encourages us to solve problems using method which can be automated. This approach promotes the application of computers beyond computer science. Wing sees computational thinking as recursive, parallel processing, choosing an appropriate representation for a problem, and modeling. Algorithms are explicitly labelled in computational thinking and involve decision steps. Many of these mental tools in computational thinking were used in Calculus for Kids, because the students had to decide how to represent problems in MAPLE and how best to model the real world.

This study grew from the Calculus for Kids work reported previously [9] with Year 6 students. That project trained teachers to use supplied multi-media materials to teach the core concepts of integral calculus and how to solve real-world problems using them. Students were provided with a copy of the MAPLE specialist mathematics software for learning and assessment. The assessment test was based on a first year engineering degree integral calculus examination.

While the overall results with Year 6 students have already been reported, some schools in our project undertook work with Year 9 students as well. This paper compares the performance of these older students with the younger ones.

3 Method

Schools were invited to become part of the project, with a teacher attending our university campus for one day of training. During the training day, we introduced the teachers to the animated Microsoft (MS) PowerPoint files they could use to teach each concept; introduced them to the ideas of integral calculus and trained them to use the MAPLE computer algebra software. MAPLE was selected over Mathematica, Microsoft Mathematics and Maxima because it used conventional notation and because we were approached by a local re-seller of the product who supported our research.

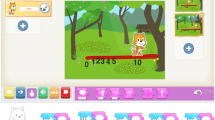
We provided a MS PowerPoint slide deck for each lesson, together with a MAPLE worksheet and a Portable Document Format (PDF) page of example questions. Students were shown how to perform simple calculations using MAPLE, starting with those they already knew (addition, subtraction, area of a rectangle) and then moved immediately to the correct terminology for setting up algebraic expressions (see Fig. 1). Integral calculus was introduced as a tool for calculating the area under a function curve. This area might represent the distance travelled for a speed-time function curve. Our basic approach was to use the strips method, whereby a curve is approximated by successively shorter straight lines. The animated MS PowerPoint slides provided powerful visual representations to illustrate the techniques of integration. While this introduction to calculus as the area under a curve was very conventional, we skipped the task of calculating examples by hand. Students were shown the integral of the sum of any number of functions is equal to the sum of the integrals of the several functions. Some ‘principles’ of integral calculus were not taught, such as manipulation of trigonometric functions, since the MAPLE software could perform this activity. Nor was differentiation discussed, since it was outside the scope of the project. Teachers were provided with a comprehensive document with solutions to all the activities.

Fig. 1.
figure 1

Example of working in MAPLE with text and mathematical expressions

Full size image

Figure 1 shows a screen from the MAPLE application. In the left-hand menu bar can be seen components for constructing mathematical expressions. The bottom-most left-hand icon is the template for a standard definite integral. When the user clicks on this icon, the template is transferred to the main page, whereupon the values of the lower bound (x1) and upper bound (x2) can be inserted. The mathematical expression for the target function ‘f’ can also be inserted to complete the definite integral. MAPLE recognises this notation and evaluates the numerical value of the integral when [CTRL] = is pressed. The MAPLE software is capable of symbolic manipulation in many other areas of mathematics. The advertising for the product claims “Maple has over 5000 functions covering virtually every area of mathematics, including calculus, algebra, differential equations, statistics, linear algebra, geometry, and much more” (www.maplesoft.com/products/Maple/features).

In the Calculus for Kids project, it is salient to recognise the software works with mathematically correct expressions and automates their calculation. From a student’s point of view, a mathematically correct expression will generate a numerical result even if the expression does not fit the related real-world example. Similarly, a notationally deficient expression will not generate a numerical result, even if it has some semblance to the real-world situation. To obtain correct results, students need to use correct mathematical notation (on-screen) and frame their algebraic expressions to precisely match the real-world problem.

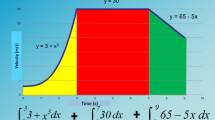
Many of the activities contained real-world problems. Since our collaboration involved academics from the Australian Maritime College, such real-world problems often involved engineering or sailing boats. Other examples involved finding the area of a billboard to be covered with a poster, finding the amount of cloth to make a curtain for a stage, the amount of metal for a drain cover, and the quantity of grass seed for a curved garden path. Students calculated the area of a sail and the amount of fabric for the curved gable end of a tent. In some cases, students were expected to devise the parabolic equation representing a real-world situation. See Fig. 2 for an example of this question type, with a student response.

Fig. 2.
figure 2

A real-world problem to be solved in the Calculus for Kids project

Full size image

To solve these real-world problems, students needed to use their computational thinking skills of modelling to formulate the curves as a mathematical expression for MAPLE. It was important to select data points which correctly matched the limits of the function to be integrated, and ensure the correct units were applied to the result. One topic relevant to this discussion was that relating to parabolic curves. We used this as an early introduction to non-linear functions, and taught how the parameters of the descriptive equation could be found from two known points on the curve. It is important to remember that students did not have to work out the value of mathematical expressions by hand. Instead, they needed their computational thinking skills to put the right parameters and equations into MAPLE, so the computer could undertake the calculation for them. This provides a new way of understanding the skill of integral calculus, and shows how computational thinking can render old methods of learning redundant.

Moving now to ways in which our results could be compared with other teaching interventions, it was previously noted that effect size is the commonly accepted measure of the impact of an innovation. It is dimensionless, and therefore allows findings from different-sized cohorts to be compared fairly. However, in the context of transformative uses of computers in schools, it has some disadvantages.

The calculation of an effect size uses the following equation [14]:

$$ \text{Effect}\;\text{Size} = \frac{{\left[ {\text{Mean}\;\text{of}\;{\text{experimental}}\;{\text{group}}} \right] - \left[ {\text{Mean}\;\text{of}\;\text{control}\;\text{group}} \right]}}{{{\text{Standard}}\;\text{Deviation}}} $$

When contemplating a transformative computer innovation, this equation can provoke speculation about the nature of the control group. Ordinarily, if students are randomly allocated to the experimental or control groups, the investigation would consider two different teaching methods. It goes without saying that the groups would be taught the same content in such a context, to show the difference in learning achievement between the two methods. However, in the current study, the definition of transformation that was adopted required new content to be taught; specifically, new content traditionally programmed for students at a much higher year level. Should the control group then comprise students in the higher year level? If so, there are two conflicting variables to consider: learning achievement and student age. If both groups are taught using the computer-based methods and tools, then it would not be easy to distinguish their impact on learning.

Another way to calculate an effect size without a control group is to compare learning achievement before and after the computer-based intervention. Where students are delivered content within the prescribed curriculum, standardised assessment tools can be used for this. However, age-accelerated transformative innovations cannot use such instruments. Therefore, Calculus for Kids used a method to calibrate each student to a notional academic year level scale. The initial measure was derived from national numeracy testing (www.myschool.edu.au), and effectively located each student as a bona-fide member of their chronological year group. Since the common post-test was derived from a first year university examination, it was possible to translate demonstrated learning achievement onto the same academic year level scale in the range Year 12–13 [9]. This study followed the same protocol. The mean numeracy score was used in conjunction with the Australia-wide mean numeracy score and standard deviation to deduce a pre-activity numeracy Year level for our students. A similar process was used to map the post-activity test score percentages onto the notional national numeracy scale, on the assumption that a 50% pass mark would map onto the Year 12/Year 13 boundary between high school and university. The demographics for the Year 6 and Year 9 samples are given in Table 1.

Table 1. Demographics for the two student groups
Full size table

There were more males in each cohort, with 54% males in the younger group, and 64% males in the older group. There was a slight overlap between the cohorts in terms of age, but at least 2 years between their mean chronological ages. This provided the opportunity to see if student age had any effect on the learning outcomes.

4 Results

Teachers of Year 9 students used the same protocols as for Year 6 students. Therefore, the three teachers attended a training session in Launceston, and then taught the material over 13 lessons (including a post-test lesson). The post-tests were sent to the research team and after marking were returned to the teachers with a community report for inclusion in newsletters to parents.

The data from each class were added to the national database for the project, and effect sizes extracted for the Year 6 and Year 9 cohorts (see Table 2).

Table 2. Effect size measures for younger and older students in the Calculus for Kids project
Full size table

Table 2 shows the numeracy aptitude for both cohorts was as expected for their respective ages. The older students demonstrated greater mastery of the high-end mathematics content than did the younger Year 6 students at the end of the intervention, but with greater variance among them.

The effect size has been calculated in three ways for each cohort. Firstly, the standard calculation using Cohen’s d is given. Then, two annual maturation measures have been used. The first uses Glass et al.’s [8] supposition that one year of learning advancement corresponds to one standard deviation. Wiliam’s refinement [15] showed annual growth in achievement between Grades 4 and 8 (as measured by standardised national testing) was 0.30 standard deviations. This has been used in the final part of the table.

5 Discussion and Conclusion

These very high effect sizes are unusual in the study of teaching innovations. However, they are derived from standard practice for comparing the effectiveness of different approaches to learning. When proponents make claims to have enacted a transformative change through the use of computers, the SAMR model predicts dramatic results, especially at the redefinition end. These very large effect sizes of 25.53 and 13.79, using Cohen’s d, justify such claims. They are well above the ‘hinge point’ of 0.4 for an effective intervention, and greater than the intervention effect size of 0.57 ascribed to computer aided instruction. It can be deduced that computer use is highly effective in schools when used to teach transformative content, and much more so than when used to teach traditional content.

The Year 9 student cohort performed in a very similar way to the Year 6 cohort. This is promising in several ways. First, it shows the original Calculus for Kids project did not accidently hit a mysterious ‘sweet spot’ which was only available for younger students for this topic of integral calculus. Second, the result validates the earlier work by showing a slightly different context does not change the outcome. Finally, it provides evidence this method of incorporating computational thinking [16] into the curriculum can be done at any age between 12 and 14 years with the same beneficial effect. Others may wish to see if these chronological boundaries can be expanded further.

To progress this work, we propose to continue working with Year 6 students using short and effective computer-based interventions involving specialist application software. Schools will be invited to participate in guided workshops that will generate specific plans appropriate for their own students. Key elements in each of the interventions will be:

  • Short in duration (typically 5 to 7 lessons).

  • Students to use a single computer software application for each intervention, generally free of cost to schools.

  • Learning outcome will be a significant departure from the existing curriculum (4–6 years in advance of chronological age).

  • Effect size will be calculated by comparing each student’s National Assessment Program – Literacy and Numeracy (NAPLAN) ranking with a calibrated post-test of learning achievement accompanied by pre- and post-activity attitudinal surveys. We will modify the Attitudes toward Mathematics Inventory [17] to make it subject-generic and link with our previous work; also, the Mathematics and Technology Attitude scale [18, 19] will be similarly adapted.

  • Participating schools will be drawn from a wide range, going beyond the 26 schools from 5 the states of Calculus for Kids, and drawing on mixed-ability classes from a range of ICSEA [socio-economic and locational status] backgrounds.

If we can demonstrate similar high effect size transformations by applying computational thinking in subjects across the breadth of the school curriculum, this would provide experimental evidence supporting curriculum change. We do not suggest every student should be taught in conjunction with a computer and powerful software in every lesson. However, there may be good reason to teach some topics, and perhaps introduce new knowledge into the curriculum where this is possible and desirable. Should we be able to demonstrate accelerated learning achievement of 4+ years with primary school students, similar processes can be put in place at other educational levels. For instance, first year undergraduates will be able to achieve learning outcomes at the Masters or even initial PhD candidate level. Year 10 students would be empowered to demonstrate understanding from first year degree courses. We seek to engender this quantum leap in learning in areas where humans working with computers can perform better than either alone. Our work with Year 6 students can be a lever for future work at all educational levels.