Tighter Security Proofs for Generic Key Encapsulation Mechanism in the Quantum Random Oracle Model

Abstract

In (TCC 2017), Hofheinz, Hövelmanns and Kiltz provided a fine-grained and modular toolkit of generic key encapsulation mechanism (KEM) constructions, which were widely used among KEM submissions to NIST Post-Quantum Cryptography Standardization project. The security of these generic constructions in the quantum random oracle model (QROM) has been analyzed by Hofheinz, Hövelmanns and Kiltz (TCC 2017), Saito, Xagawa and Yamakawa (Eurocrypt 2018), and Jiang et al. (Crypto 2018). However, the security proofs from standard assumptions are far from tight. In particular, the factor of security loss is q and the degree of security loss is 2, where q is the total number of adversarial queries to various oracles.

In this paper, using semi-classical oracle technique recently introduced by Ambainis, Hamburg and Unruh (ePrint 2018/904), we improve the results in (Eurocrypt 2018, Crypto 2018) and provide tighter security proofs for generic KEM constructions from standard assumptions. More precisely, the factor of security loss q is reduced to be $\sqrt{q}$. In addition, for transformation T that turns a probabilistic public-key encryption (PKE) into a determined one by derandomization and re-encryption, the degree of security loss 2 is reduced to be 1. Our tighter security proofs can give more confidence to NIST KEM submissions where these generic transformations are used, e.g., CRYSTALS-Kyber etc.

Appendices

A Cryptographic Primitives

Definition 1

(Public-key encryption). A public-key encryption scheme $\mathrm {PKE}$ consists of three algorithms. The key generation algorithm, Gen, is a probabilistic algorithm which on input $1^{\lambda }$ outputs a public/secret key-pair (pk, sk). The encryption algorithm Enc, on input pk and a message $m \in \mathcal {M}$, outputs a ciphertext $c\leftarrow Enc(pk,m)$. If necessary, we make the used randomness of encryption explicit by writing $c:=Enc(pk,m;r)$, where $r \overset{\$}{\leftarrow } \mathcal {R}$ ($\mathcal {R}$ is the randomness space). The decryption algorithm Dec, is a deterministic algorithm which on input sk and a ciphertext c outputs a message $m:=Dec({sk},c)$ or a rejection symbol $\perp \notin \mathcal {M}$. A PKE is determined if Enc is deterministic. We denote $\mathrm {DPKE}$ to stand for a determined PKE.

Definition 2

(Correctness [4]). A public-key encryption scheme $\mathrm {PKE}$ is $\delta$-correct if $E[\mathop {\mathrm {max}}\limits _{m\in \mathcal {M}}\Pr [Dec(sk,c)\ne m : c \leftarrow Enc(pk,m)]]\le \delta ,$ where the expectation is taken over $(pk,sk) \leftarrow Gen$. A PKE is perfectly correct if $\delta =0$.

Definition 3

(DS-secure DPKE [10]). Let $D_\mathcal {M}$ denote an efficiently sampleable distribution on a set $\mathcal {M}$. A DPKE scheme (Gen,Enc,Dec) with plaintext and ciphertext spaces $\mathcal {M}$ and $\mathcal {C}$ is $D_\mathcal {M}$-disjoint simulatable if there exists a PPT algorithm S that satisfies the following,

• (1) Statistical disjointness:

  $$\begin{aligned} {\textsc {Disj}}_{\mathrm {PKE},S}:=\mathop {\max }\limits _{(pk,sk)\in Gen(1^\lambda ;\mathcal {R}_{gen})} \Pr [c\in Enc(pk,\mathcal {M}): c \leftarrow S(pk)] \end{aligned}$$

  is negligible, where $\mathcal {R}_{gen}$ denotes a randomness space for Gen.

• (2) Ciphertext indistinguishability: For any PPT adversary ,

  

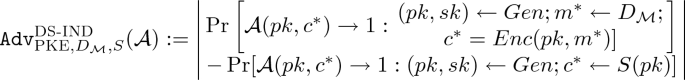
  is negligible.

Fig. 6.

Games OW-ATK (ATK $\in$ {CPA, VA, qPCA, qPVCA}) for PKE, where $O_{\mathrm {ATK}}$ is defined in Definition 4. In games qPCA and qPVCA, the adversary can query the $\textsc {Pco}$ oracle with quantum state.

Fig. 7.

IND-CPA game for PKE and IND-CCA game for KEM.

Definition 4

(OW-ATK-secure PKE). Let $\mathrm {PKE}=(Gen, Enc, Dec)$ be a public-key encryption scheme with message space $\mathcal {M}$. For $\mathrm {ATK} \in \{\mathrm {CPA,VA,}$ $\mathrm {qPCA,qPVCA}\}$ [11], we define $\text{ OW-ATK }$ games as in Fig. 6, where

Define the OW-ATK advantage function of an adversary against PKE as .

Definition 5

(IND-CPA-secure PKE). Define $\mathrm {IND-CPA}$ game of PKE as in Fig. 7 and the $\mathrm {IND-CPA}$ advantage function of an adversary against PKE as .

Definition 6

(Key encapsulation). A key encapsulation mechanism KEM consists of three algorithms. The key generation algorithm Gen outputs a key pair (pk, sk). The encapsulation algorithm Encaps, on input pk, outputs a tuple (K, c), where $K \in \mathcal {K}$ and c is said to be an encapsulation of the key K. The deterministic decapsulation algorithm Decaps, on input sk and an encapsulation c, outputs either a key $K := Decaps(sk, c) \in \mathcal {K}$ or a rejection symbol $\perp \notin \mathcal {K}$.

Definition 7

(IND-CCA-secure KEM). We define the $\mathrm {IND-CCA}$ game as in Fig. 7 and the $\mathrm {IND-CCA}$ advantage function of an adversary against $\mathrm {KEM}$ as .

B Proof of Theorem 2

Proof

Let be an adversary against the OW-qPCA security of PKE$'$, issuing at most $q_{PC}$ queries to the oracle PCO, at most $q_G$ queries to the random oracle $G$. Denote $\varOmega _G$ as the sets of all functions $G:\mathcal {M} \rightarrow \mathcal {R}$. Let $G'$ be a random function such that $G'(m)$ is sampled according to the uniform distribution in $\mathcal {R}_{\mathrm {good}}(pk,sk,m)$, where $\mathcal {R}_{\mathrm {good}}(pk,sk,m):=\{{r \in \mathcal {R}}: Dec(sk,Enc(pk,m;r))= m\}$. Let $\varOmega _{G'}$ be the set of all functions $G'$. Let as the fraction of bad randomness, where $\mathcal {R}_{\mathrm {bad}}(pk,sk,m)=\mathcal {R}\setminus \mathcal {R}_{\mathrm {good}}(pk,sk,m)$. $\delta (pk,sk)=\max _{m\in {\mathcal {M}}}\delta (pk,sk,m)$. $\delta =\mathbf {E}[\delta (pk,sk)]$, where the expectation is taken over $(pk,sk) {\leftarrow }Gen$. Consider the games in Figs. 8 and 9.

Game $G_0$. Since game $G_0$ is exactly the OW-qPCA game,

Fig. 8.

Games $G_0$-$G_6$ for the proof of Theorem 2

Fig. 9.

Game $G_6$ and game $G_7$ for the proof of Theorem 2

Game $G_1$. In game $G_1$, we replace G by $G'$ that uniformly samples from “good” randomness at random, i.e., $G' \overset{\$}{\leftarrow } \varOmega _{G'}$. Following the same analysis as in the proof of Theorem 1, we can have

Game $G_2$. In game $G_2$, the $\textsc {PCO}$ oracle is changed that it makes no use of the secret key any more. Particularly, when queries PCO oracle, $Enc(pk,m;G(m))=?c$ is returned instead of $Dec'(sk,c)=?m$. It is easy to verify that $Dec'(sk,c)=?m$ is equal to $Dec(sk,c)=?m \wedge Enc(pk,m;G(m))=?c$. Thus, the outputs of the PCO oracles in $G_1$ and $G_2$ merely differs for the case of $Dec(sk,c)\ne m$ and $Enc(pk,m;G(m))=c$. But, such a case does not exist since G in this game only samples from “good” randomness. That is, the PCO oracle in $G_2$ always has the identical output with the one in $G_1$. Therefore, we have

Game $G_3$. In game $G_3$, we switch the G that only samples from “good” randomness back to an ideal random oracle G. Then, similar to the case of $G_0$ and $G_1$, the distinguishing problem between $G_2$ and $G_3$ can also be converted to the distinguishing problem between G and $G'$. Using the same analysis method in bounding the difference between $G_0$ and $G_1$, we can have

Game $G_4$. In game $G_4$, an additional query to G with classical state $|m'\rangle |0\rangle$ is performed after returns $m'$. Obviously, $G_4$ has the same output as $G_3$ and we have

Let $\ddot{G}$ be the function that $\ddot{G}(m^*)=\ddot{r}^*$, and $\ddot{G}=G$ everywhere else, where $\ddot{r}^*$ is picked uniformly at random from $\mathcal {R}$.

Game $G_5$. In game $G_5$, we replace G by a semi-classical oracle $\ddot{G}\backslash {m^*}$. For a query input, $\ddot{G}\backslash {m^*}$ will first query $\mathcal {O}_{m^*}^{{SC}}$, i.e., perform a semi-classical measurement, and then query $\ddot{G}$. Let Find be the event that $\mathcal {O}_{{m^*}}^{SC}$ ever outputs 1 during semi-classical measurements of the queries to $\ddot{G}\backslash {m^*}$. We note that

since implies that $m'=m^*$ in $G_5$, and $\ddot{G}$ is classically queried at $m'$ in $G_5$⁵. Applying Lemma 3 with $X={\mathcal {M}}$, $Y=\mathcal {R}$, $S=\{m^*\}$, $\mathcal {O}_1=G$, $\mathcal {O}_2=\ddot{G}$ and $z=(pk, c^*)$, we can have

Game $G_6$. In game $G_6$, we replace $r^*:=G(m^*)$ by $r^*\overset{\$}{\leftarrow } \mathcal {R}$. Since $G(m^*)$ is only used once and independent of the oracles $\ddot{G}$ and PCO,

$$\begin{aligned} \Pr [\textsf {Find } : G_5]=\Pr [\textsf {Find } : G_6]. \end{aligned}$$

Note that $G(m^*)$ is never used in $G_6$, we can just replace $G \overset{\$}{\leftarrow } \varOmega _G;\ddot{G}=G;\ddot{G}(m^*)\overset{\$}{\leftarrow } \mathcal {R}$ by $\ddot{G} \overset{\$}{\leftarrow } \varOmega _G$. For brevity and readability, we will substitute the notation $\ddot{G}$ with notation G. Then, game $G_6$ can be rewritten as in Fig. 9.

Game $G_7$. In game $G_7$, we replace $c^*=Enc(pk,m^*;r^*)$ by $c^*=Enc(pk,m_1^*;r^*)$, where $m_1^*\overset{\$}{\leftarrow } \mathcal {M}$. Note that the information of $m^*$ in this game only exists in the oracle ${{G}} \backslash {m^*}$, by Lemma 4 we have

Next, we show that any adversary distinguishing $G_6$ from $G_7$ can be converted into an adversary against the IND-CPA security of underlying PKE scheme. Construct an adversary on input ($1^\lambda$, pk) as in Fig. 10, where $\textsf {Find }$ is 1 iff the event $\textsf {Find }$ that $\mathcal {O}_{{m_0}}^{SC}$ ever outputs 1 during semi-classical measurements of the queries to ${G}\backslash {m_0}$ happens. Then, according to Lemma 1, if $b''=0$, perfectly simulates $G_6$ and . If $b''=1$, perfectly simulates $G_7$ and . Since

Fig. 10.

Adversary for the proof of Theorem 2

Finally, combing this with the bounds derived above, we can conclude that

   $\square$