Abstract
In a series of early essays written around 1679, Leibniz sets out to explore the logic of conceptual containment. In his more mature logical writings from the mid-1680s, however, his focus shifts away from the logic of containment to that of coincidence, or mutual containment. This shift in emphasis is indicative of the fact that Leibniz’s logic has its roots in two distinct theoretical frameworks: (i) the traditional theory of the categorical syllogism based on rules of inference such as Barbara, and (ii) equational systems of arithmetic and geometry based on the rule of substitution of equals. While syllogistic reasoning is naturally modeled in a logic of containment, substitutional reasoning of the sort performed in arithmetic and geometry is more naturally modeled in a logic of coincidence. In this paper, we argue that Leibniz’s logic of conceptual containment and his logic of coincidence can in fact be viewed as two alternative axiomatizations, in different but equally expressive languages, of one and the same logical theory. Thus, far from being incoherent, the varying syllogistic and equational themes that run throughout Leibniz’s logical writings complement one another and fit together harmoniously.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In what follows, we adopt the following abbreviations for editions of Leibniz’s writings:
- A:
-
Gottfried Wilhelm Leibniz: Sämtliche Schriften und Briefe. Ed. by the Berlin-Brandenburgische Akademie der Wissenschaften and the Akademie der Wissenschaften zu Göttingen, Berlin: de Gruyter. Cited by series, volume, and page.
- C:
-
Opuscules et fragments inédits de Leibniz. Ed. by L. Couturat, Paris: Félix Alcan, 1903.
- GM:
-
Leibnizens mathematische Schriften. Ed. by C. I. Gerhardt, Halle: H. W. Schmidt, 1849–63. Cited by volume and page.
- GP:
-
Die philosophischen Schriften von Gottfried Wilhelm Leibniz. Ed. by C. I. Gerhardt, Berlin: Weidmann, 1875–90. Cited by volume and page.
In addition, we sometimes use the abbreviation ‘GI’ for Leibniz’s essay Generales inquisitiones de analysi notionum et veritatum (A VI.4 739–88). This essay consists of a series of numbered sections, which we designate by references such as ‘GI §16’ and ‘GI §72’.
- 2.
- 3.
A VI.4 223; see also A VI.4 218 n. 1, 551, GI §132.
- 4.
See A VI.4 148–50.
- 5.
A VI.4 119–20, 140–5, and 280–8; see also A VI.4 274–9.
- 6.
GI §157 and §163. Accordingly, the axioms of the calculus developed by Leibniz in the Generales inquisitiones almost all take the form of coincidence propositions; see the preliminary axiomatizations of the calculus in GI §§1–15, §171, and §189, as well as the final axiomatization in §198.
- 7.
GI §83, §113, A VI.4 751 n. 13, 808. For other definitions of containment in terms of coincidence, see GI §16, §17, §189.4, and §198.9.
- 8.
- 9.
A VI.4 807–14, 816–22, 830–45; see also A VI.4 845–55 and C 421–3. Prior to the Generales inquisitiones, no systematic attempt is made by Leibniz to develop a calculus of coincidence. As far as we can see, the earliest indication of Leibniz’s desire to develop such a calculus appears in an essay written around 1685 titled Ad Vossii Aristarchum (see A VI.4 622–4).
- 10.
See A VI.4 1539–41, 1644, and VI.6 396–8.
- 11.
See GI §198.9.
- 12.
A VI.4 622.
- 13.
GI §30, §88, and §195; see also A VI.4 813.
- 14.
In some of his earlier essays, Leibniz seems to employ an object language which includes primitive propositional operators for implication and conjunction (see, e.g., A VI.4 127–31, 142–3, 146–50). In his mature logical writings, however, Leibniz does not include such propositional operators in the object language of his calculi (see, e.g., the coincidence calculi formulated at GI §§198–200, A VI.4 816–22, 830–55). In the Generales inquisitiones, for example, Leibniz formulates his calculus in an object language in which every proposition is of the form A coincides with B (see Castañeda 1976: 483–4, Malink and Vasudevan 2016: 689–96). This decision to abstain from the use of primitive propositional operators is not an arbitrary choice on Leibniz’s part, but is an essential part of his broader theoretical ambition to reduce propositional logic to a categorical logic of terms and, in particular, to ‘reduce hypothetical to categorical propositions’ (A VI.4 992; see also GI §75, §137, VI.4 811 n. 6, 862–3). For Leibniz’s commitment to the Peripatetic program of reducing propositional to categorical logic, see Barnes 1983: 281 and Malink and Vasudevan 2018: §1.
- 15.
- 16.
This strategy for deriving laws of coincidence from underlying laws of containment is adopted, for example, by Schröder (1890: 184–5). There are, in fact, a number of striking parallels between Leibniz’s containment calculus and Schröder’s algebraic system of logic (see nn. 24, 34, and 38 below).
- 17.
This presupposes that the introduction and elimination rules for coincidence are conservative in the sense that they do not allow us to derive any new theorems of the form A is B not already derivable in the underlying containment calculus. For, if these rules were not conservative, the newly introduced concept of coincidence would have, as Brandom puts it, ‘substantive content …that is not already implicit in the contents of the other concepts being employed’ (Brandom 1994: 127, 2000: 71). If, on the other hand, coincidence is introduced by means of conservative introduction and elimination rules, then ‘no new content is really involved’ (Brandom 1994: 127, 2000: 71). In this way, the connective of coincidence can be introduced into a pure containment calculus without the need to rely on ‘an antecedent idea of the independent meaning of the connective’ (Belnap 1962: 134; see also Dummett 1991: 247). This condition of conservativity is satisfied for all the versions of Leibniz’s containment calculus discussed in this paper.
- 18.
The rule of substitution also appears as the first principle listed by Leibniz in many subsequent versions of the coincidence calculus (see, e.g., A VI.4 810, 816, 831, 846). For further statements of the rule of substitution, see GI §9, §19, A VI.4 626, 746.
- 19.
It is easy to verify that, given the introduction and elimination rules for coincidence, this rule of substitution for containment implies the general rule of substitution for the extended language of Leibniz’s containment calculus, i.e.:
 , where φ is any proposition of the form C ⊃ D or C = D.
, where φ is any proposition of the form C ⊃ D or C = D. - 20.
See, e.g., A VI.4 154, 275, 284, 294.
- 21.
See, e.g., A VI.4 144, 154, 275, 281, 293, 497, 551.
- 22.
See, e.g., A VI.4 280–1, GI §47, §124, §129, §§190–1.
- 23.
See A VI.4 282.
- 24.
For a similar proof of the rule of substitution based on Barbara in a containment calculus, see Schröder 1890: 186.
- 25.
A VI.4 809; cf. A VI.4 143–5, 154, 275, 672.
- 26.
In his essay Principia calculi rationalis, for example, Leibniz provides the following substitutional proof of Barbara based on his definition of A ⊃ B as A = AB (C 229–30). Suppose A = AB and B = BC (i.e., A ⊃ B and B ⊃ C). Substituting BC for B in the former proposition yields A = ABC. Substituting AB for A in this last proposition yields A = AC (i.e., A ⊃ C). For similar substitutional proofs of Barbara, see GI §19 and A VI.4 813. A substitutional proof of Barbara along these lines is also given by Jevons (1869: 29–30).
- 27.
In the Elementa ad calculum condendum, this law is stated at A VI.4 154. For other statements of this law, see, e.g., A VI.4 148, 149, 150, 151, 274, 280, 292, 813.
- 28.
We have omitted items (5) and (6) from this list since they do not contain principles of the calculus, but theorems which Leibniz derives from the principles stated in (1)–(4).
- 29.
In item (3), Leibniz asserts only a restricted version of weakening in which the propositions φ and ψ have a term in common. This restriction, however, is likely inadvertent, since Leibniz asserts the rule of weakening in full generality immediately before the list of principles quoted above: ‘A is B and C is D, therefore A is B’ (A VI.4 149).
- 30.
This is clear, for example, from the way in which Leibniz derives the theorem A = B, B = C, C = D ⊢ A = D in his coincidence calculus by two consecutive applications of A = B, B = C ⊢ A = C (A VI.4 831). In this derivation, Leibniz employs the following instance of cut: if A = C, C = D ⊢ A = D and A = B, B = C ⊢ A = C, then A = B, B = C, C = D ⊢ A = D. See also the application of cut at A VI.4 837.
- 31.
Monotonicity asserts that, if Γ ⊢ φ, then Γ ∪ Δ⊢ φ. The structural rules of cut and weakening imply this principle for the case in which Γ and Δ are finite sets of propositions. To see this, we first establish monotonicity for the case in which Γ is empty and Δ is the singleton set {ψ}, i.e.: if ⊢ φ, then ψ ⊢ φ. By weakening, we have φ, ψ ⊢ φ. Hence, given ⊢ φ, it follows by cut that ψ ⊢ φ. Next, we establish monotonicity for the case in which Γ is non-empty and Δ is the singleton set {ψ}, i.e.: if Γ ⊢ φ and Γ ≠ ∅, then Γ ∪{ψ}⊢ φ. Let χ be any proposition in Γ. By weakening, we have χ, ψ ⊢ χ. Hence, given Γ ⊢ φ, it follows by cut that Γ ∪{ψ}⊢ φ. The finite version of monotonicity, in which Γ and Δ are any finite sets of propositions, follows immediately from these two cases. Thus, Leibniz’s containment calculus is finitely monotonic. For the sake of simplicity, we will also assume that the calculus is monotonic under the addition of infinitely many premises, although this assumption plays no essential role in what follows and can be freely omitted.
- 32.
In his formulation of these principles, Leibniz takes the phrases ‘A is B’ and ‘Every A is B’ to be equivalent (see n. 22). This can be seen from the proof given by Leibniz in item (6) of his list, where he takes Every AB is A to entail AB is A, and, conversely, takes AB is C to entail Every AB is C (A VI.4 150).
- 33.
Moreover, C3 is explicitly stated by Leibniz at A VI.4 274–5, 281, GI §38, §39, §46.
- 34.
In fact, in order to establish Theorem 6, it is not necessary to appeal to Theorem 4 but only to the following weaker version of this theorem:
$$\displaystyle \begin{aligned} \begin{array}{rcl} A\supset C, C\supset A, B\supset D, D\supset B\vdash_{\mathrm{c}} AB\supset CD \end{array} \end{aligned} $$Given the introduction and elimination rules for coincidence, this is equivalent to the following law asserting that coincidence is a congruence relation with respect to the operation of composition:
$$\displaystyle \begin{aligned} \begin{array}{rcl} A=C, B=D \vdash_{\mathrm{c}} AB=CD \end{array} \end{aligned} $$Schröder (1890: 270) appeals to this latter law to establish a variant of Theorem 6 in his containment calculus.
- 35.
- 36.
Leibniz does on a few separate occasions discuss privative terms in his earlier logical writings (e.g., A VI.4 218, 224, 253, 292–7, 622). The first systematic treatment of these terms, however, appears in the Generales inquisitiones.
- 37.
A VI.4 146.
- 38.
In fact, in order to establish Theorem 9, it is not necessary to appeal to the law of contraposition but only to the following weaker version of this law:
$$\displaystyle \begin{aligned} \begin{array}{rcl} A\supset B, B\supset A \vdash_{\mathrm{cp}} \overline{B}\supset\overline{A} \end{array} \end{aligned} $$Given the introduction and elimination rules for coincidence, this is equivalent to the following law asserting that coincidence is a congruence relation with respect to the operation of privation:
$$\displaystyle \begin{aligned} \begin{array}{rcl} A=B \vdash_{\mathrm{cp}} \overline{A}=\overline{B} \end{array} \end{aligned} $$Schröder (1890: 306) appeals to this latter law to establish a variant of Theorem 9 in his containment calculus.
- 39.
- 40.
See, e.g., GI §2, §96, §171.4, §189.2, §198.3, A VI.4 218, 624, 740, 807, 811, 814, 877, 931, 935, 939, C 230, 235, 421.
- 41.
See GI §55, §193–4, §197, A VI.4 774 n. 47, 807, 813. In the Generales inquisitiones, Leibniz uses a number of phrases interchangeably to expresses the non-being, or falsehood, of a given term A, e.g.: ‘A is not’ (GI §§149–50, §§199–200), ‘A is not a thing’ (GI §§149–55, §171.8), ‘A is a non-being’ (GI §32b, §55, A VI.4 810 n. 5, 813, 875, 930, 935), ‘A is false’ (GI §55, §§58–9, §189.3, §§193–5, §197, §198.4, A VI.4 939), ‘A is impossible’ (GI §32b, §§33–4, §55, §128, A VI.4 749 n. 11, 807, 875, 930, 935, 939).
- 42.
For similar statements of this equivalence, see A VI.4 862–3 and C 237.
- 43.
In the Generales inquisitiones, Leibniz explores the possibility of expressing existential quantification in the language of his calculus by means of what he calls ‘indefinite letters’ (§§16–31; see Lenzen 1984b: 7–13, 2004: 47–50, Hailperin 2004: 329). However, the introduction of indefinite letters into the calculus gives rise to complications analogous to those which arise in connection with the elimination of existential quantifiers in modern quantificational logic (see, e.g., GI §§21–31). Leibniz was aware of some of these complications and was never entirely satisfied with the use of indefinite letters, indicating that it would be preferable to omit them from the language of his calculus (see GI §162 in conjunction with §128 and A VI.4 766 n. 35; cf. Schupp 1993: 153, 168, 182–3). In the absence of indefinite letters, the language of Leibniz’s calculus lacks the resources to express existential quantification.
- 44.
See the proof of Theorem 21.i in the appendix.
- 45.
See Theorem 21.iii in the appendix.
- 46.
- 47.
See GI §75, §109, §197. When a proposition is conceived of as a term, Leibniz describes the proposition as giving rise to a ‘new term’ (terminus novus, §197 and §198.7; contra Parkinson 1966: 86 n. 2).
- 48.
See GI §§138–42 and A VI.4 740.
- 49.
- 50.
Similarly, Leibniz writes that ‘whatever is said of a term which contains a term can also be said of a proposition from which another proposition follows’ (§189.6). See also §138, VI4A 809, 811 n. 6, 863; cf. Swoyer 1995: 110.
- 51.
To justify the claim that one proposition follows (sequitur) from another, Leibniz often provides a derivation of the former from the latter in his calculus (e.g., §49, §§52–4, §100). Moreover, there is no indication that Leibniz entertained the possibility that a proposition might follow from another despite not being derivable from it in his calculus. On the contrary, he asserts the completeness of the principles of his calculus when he states that ‘whatever cannot be demonstrated from these principles does not follow by virtue of logical form’ (§189.7).
- 52.
See Theorem 4.53 in Malink and Vasudevan 2016: 738.
- 53.
In an earlier paper, we claimed that the validity of substitutions within propositional terms can be justified by the weak principle of propositional containment asserting that φ ⊢ ψ just in case \(\vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\psi }\urcorner \) (Malink and Vasudevan 2016: 697 n. 41 and 702 n. 66). This claim, however, is not correct. In order to establish the validity of substitutions within propositional terms, one in fact needs the following two-premise version of the principle of propositional containment: φ, ψ ⊢ χ just in case \(\varphi \vdash \ulcorner {\psi }\urcorner \supset \ulcorner {\chi }\urcorner \). Now, there is independent textual evidence that Leibniz endorses this two-premise version of the principle (see Malink and Vasudevan 2018: §3). Thus, Leibniz is committed to the validity of substitutions within propositional terms. This comports well with the fact that, in his various statements of the rule of substitution in the Generales inquisitiones and elsewhere, Leibniz gives no indication that this rule is to be restricted to syntactic contexts that do not occur within propositional terms (see, e.g., GI §198.1, A VI.4 746, 810, 816, 831, 846).
- 54.
For a similar statement of this principle, see A VI.4 809.
- 55.
The fact that Leibniz applies the term-operation of privation to B indicates that B is a term. Moreover, the fact that he characterizes B as a proposition strongly suggests that B is, more specifically, a propositional term.
- 56.
See Theorem 29 in the appendix.
- 57.
This weaker version of the principle of propositional containment suffices to establish the classical laws of conjunction in the calculus ⊢ (see the proof of Theorem 29 in the appendix). Given these laws, it can be shown that this weaker version of the principle entails the strong version for those cases in which Γ is a finite set of propositions. For, given the rule of conjunction-introduction, all the propositions in the finite set Γ can be conjoined into a single proposition, to which the weaker version of the principle can be applied. This conjunctive proposition can then be unpacked again by the rule of conjunction-elimination. The extension to cases in which Γ is infinite follows from monotonicity and the fact that a proposition is derivable from an infinite set of premises in the calculus ⊢ just in case it is derivable from some finite subset of this set.
- 58.
Up to a change of signature, auto-Boolean algebras just are what are known as simple monadic algebras (cf. Halmos 1962: 40–8; Goldblatt 2006: 14). These are Boolean algebras equipped with an additional unary operation f defined by:
$$\displaystyle \begin{aligned} \begin{array}{rcl} f(x) = \left\{\begin{array}{ll} 0 &\displaystyle {\quad } \text{if}\\ x=0\\ 1 &\displaystyle {\quad }\text{otherwise}\end{array}\right. \end{array} \end{aligned} $$An auto-Boolean algebra is a simple monadic algebra in which the operation f is defined by f(x) = (x ∘ 0) ∘ 0. Conversely, a simple monadic algebra is an auto-Boolean algebra in which the operation ∘ is defined by x ∘ y = (f((x′∧ y) ∨ (y′∧ x)))′.
- 59.
For a proof of this claim, see Theorem 44 in the appendix.
- 60.
- 61.
For a proof of this claim, see Theorem 37 below.
- 62.
- 63.
See n. 18 above.
- 64.
A VI.4 154.
- 65.
- 66.
See A VI.1 179–87.
- 67.
See the references given in n. 22 above.
- 68.
See Netz 1999: 189–97. Netz argues that in Greek mathematics ‘the concept of substitution salva veritate is the key to most proofs’ (1999: 190).
- 69.
See Netz 1999: 191.
- 70.
By contrast, an explicit statement of the rule of substitution was included in some seventeenth-century axiomatizations of Euclid’s Elements (see De Risi 2016b: 618–24).
- 71.
For Leibniz’s desire to provide demonstrations of Euclid’s common notions, see De Risi 2016a: 25 n. 7, 31 n. 17, 33 n. 19.
- 72.
See also A II.1 769, GM 7 274.
- 73.
See, e.g., A VI.4 165-7, 506–7, GM 5 156, GM 7 77–80.
- 74.
For similar substitutional proofs of the transitivity of coincidence, see A VI.4 750, 815, 816, 849.
- 75.
In our translation of this passage, we print ‘=’ in place of Leibniz’s symbol ‘∞’, the former being the symbol that Leibniz uses in the Generales inquisitiones to express the relation of coincidence between terms.
- 76.
The coincidence calculus developed by Leibniz in the Specimen calculi coincidentium et inexistentium is intended to be an abstract calculus that admits of multiple interpretations. In particular, Leibniz intends the calculus to be applicable to any algebraic structure which satisfies the laws of commutativity and idempotence, AB = BA and AA = A (A VI.4 834). As Leibniz explains, the law of idempotence excludes arithmetical interpretations of the calculus (A VI.4 834; see also GI §129, A VI.4 512 and 811). At the same time, Leibniz points out that the calculus is applicable to the domain of terms, or concepts (notiones), when ‘=’ is taken to expresses the relation of coincidence, and the concatenation of letters is taken to express the operation of composition on terms (see Swoyer 1994: 7 and 18; Lenzen 2000: 79–82; Mugnai 2017: 175–6).
- 77.
Jevons 1887: 17.
- 78.
Similarly, Jevons writes: ‘it is not difficult to show that all forms of reasoning consist in repeated employment of the universal process of the substitution of equals’ (Jevons 1869: 23–4).
- 79.
Jevons 1887: xvi.
- 80.
Jevons 1887: xvii–xviii. The derivations of the laws of coincidence given by Leibniz in this essay follow exactly the same pattern as his derivations of these laws in the Specimen calculi coincidentium et inexistentium referred to above (cp. A VI.4 831–7 with A VI.4 846–50).
- 81.
Jevons 1887: xviii.
- 82.
This essay appears at GP 7 208–10. It also appears under the title De syllogismo categorico ex inclusione exclusioneve terminorum in a preliminary volume of the Academy edition (Vorausedition A VI.5 1120). The editors of this volume date the essay between 1690 and 1696.
- 83.
A VI.4 812.
- 84.
See Section 1.1 above.
- 85.
The ‘demonstration’ referred to in this passage appears at Peirce 1873: 318 n. 1.
Bibliography
Adams, R.M. 1994. Leibniz: Determinist, Theist, Idealist. New York: Oxford University Press.
Barnes, J. 1983. Terms and sentences. Proceedings of the British Academy 69: 279–326.
Belnap, N. 1962. Tonk, plonk and plink. Analysis 22: 130–134.
Birkhoff, G. 1935. On the structure of abstract algebras. Mathematical Proceedings of the Cambridge Philosophical Society 31: 433–454.
Brandom, R.B. 1994. Making It Explicit: Reasoning, Representing, and Discursive Commitment. Cambridge, MA: Harvard University Press.
Brandom, R.B. 2000. Articulating Reasons: An Introduction to Inferentialism. Cambridge, MA: Harvard University Press.
Byrne, L. 1946. Two brief formulations of Boolean algebra. Bulletin of the American Mathematical Society 52: 269–272.
Castañeda, H.-N. 1976. Leibniz’s syllogistico-propositional calculus. Notre Dame Journal of Formal Logic 17: 481–500.
Couturat, L. 1901. La logique de Leibniz. Paris: Félix Alcan.
De Risi, V. 2016a. Leibniz on the Parallel Postulate and the Foundations of Geometry: The Unpublished Manuscripts. Heidelberg: Birkhäuser.
De Risi, V. 2016b. The development of Euclidean axiomatics: The systems of principles and the foundations of mathematics in editions of the elements in the early modern age. Archive for History of Exact Sciences 70: 591–676.
Dummett, M.A.E. 1991. The logical Basis of Metaphysics. Cambridge, MA: Harvard University Press.
Goldblatt, R. 2006. Mathematical modal logic: A view of its evolution. In Logic and the Modalities in the Twentieth Century, Handbook of the History of Logic, vol. 7, ed. D.M. Gabbay and J. Woods, 1–98. Amsterdam: Elsevier.
Hailperin, T. 2004. Algebraical logic 1685–1900. In The Rise of Modern Logic: From Leibniz to Frege, Handbook of the History of Logic, vol. 3, ed. D.M. Gabbay and J. Woods, 323–388. Amsterdam: Elsevier.
Halmos, P.R. 1962. Algebraic Logic. New York: Chelsea Publishing Company.
Jevons, W.S. 1869. The Substitution of Similars: The True Principle of Reasoning. London: Macmillan.
Jevons, W.S. 1887. The Principles of Science: A Treatise on Logic and Scientific Method, 2nd ed. London: Macmillan.
Lenzen, W. 1984a. Leibniz und die Boolesche Algebra. Studia Leibnitiana 16: 187–203.
Lenzen, W. 1984b. „Unbestimmte Begriffe“ bei Leibniz. Studia Leibnitiana 16: 1–26.
Lenzen, W. 1986. ‚Non est‘ non est ‚est non‘. Zu Leibnizens Theorie der Negation. Studia Leibnitiana 18: 1–37.
Lenzen, W. 1987. Leibniz’s calculus of strict implication. In Initiatives in Logic, ed. J. Srzednicki, 1–35. Dordrecht: Kluwer.
Lenzen, W. 1988. Zur Einbettung der Syllogistik in Leibnizens “Allgemeinen Kalkül”. In Leibniz: Questions de logique, ed. A. Heinekamp, 38–71. Stuttgart: Steiner Verlag.
Lenzen, W. 2000. Guilielmi Pacidii Non plus ultra, oder: Eine Rekonstruktion des Leibnizschen Plus-Minus-Kalküls. Logical Analysis and History of Philosophy 3: 71–118.
Lenzen, W. 2004. Leibniz’s logic. In The Rise of Modern Logic: From Leibniz to Frege, Handbook of the History of Logic, vol. 3, ed. D.M. Gabbay and J. Woods, 1–83. Amsterdam: Elsevier.
Malink, M., and A. Vasudevan. 2016. The logic of Leibniz’s Generales inquisitiones de analysi notionum et veritatum. Review of Symbolic Logic 9: 686–751.
Malink, M., and A. Vasudevan. 2018. The peripatetic program in categorical logic: Leibniz on propositional terms. Review of Symbolic Logic. https://doi.org/10.1017/S1755020318000266.
Mugnai, M. 2017. Leibniz’s mereology in the essays on logical calculus of 1686–90. In Für unser Glück oder das Glück Anderer: Vorträge des X. Internationalen Leibniz-Kongresses, Band VI, ed. W. Li, 175–194. Hildesheim: Olms Verlag.
Netz, R. 1999. The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History. Cambridge: Cambridge University Press.
Parkinson, G.H.R. 1965. Logic and Reality in Leibniz’s Metaphysics. Oxford: Clarendon Press.
Parkinson, G.H.R. 1966. Gottfried Wilhelm Leibniz: Logical Papers. A Selection. Oxford: Clarendon Press.
Peirce, C.S. 1873. Description of a notation for the logic of relatives, resulting from an amplification of the conceptions of Boole’s calculus of logic. Memoirs of the American Academy of Arts and Sciences 9: 317–378.
Peirce, C.S. 1880. On the algebra of logic. American Journal of Mathematics 3: 15–57.
Peirce, C.S. 1984. Writings of Charles S. Peirce: A Chronological Edition, Volume 2: 1867–1871. Bloomington: Indiana University Press.
Pertz, G.H. 1847. Leibnizens gesammelte Werke aus den Handschriften der Königlichen Bibliothek zu Hannover I.4. Hannover: Hahn.
Schröder, E. 1890. Vorlesungen über die Algebra der Logik (erster Band). Leipzig: Teubner.
Schupp, F. 1993. Gottfried Wilhelm Leibniz: Allgemeine Untersuchungen über die Analyse der Begriffe und Wahrheiten, 2nd ed. Hamburg: Felix Meiner.
Sommers, F. 1982. The Logic of Natural Language. Oxford: Clarendon Press.
Sommers, F. 1993. The world, the facts, and primary logic. Notre Dame Journal of Formal Logic 34: 169–182.
Swoyer, C. 1994. Leibniz’s calculus of real addition. Studia Leibnitiana 26: 1–30.
Swoyer, C. 1995. Leibniz on intension and extension. Noûs 29: 96–114.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Algebraic Semantics for Leibniz’s Containment Calculi
Appendix: Algebraic Semantics for Leibniz’s Containment Calculi
In this appendix, we provide an algebraic semantics for the containment calculi ⊢c, ⊢cp, and ⊢ (introduced in Definitions 3, 12, and 16 above). The three main results established in this appendix are:
-
The calculus ⊢c is sound and complete with respect to the class of semilattices (Theorem 20).
-
The calculus ⊢cp is sound and complete with respect to the class of Boolean algebras (Theorem 25).
-
The calculus ⊢ is sound and complete with respect to the class of auto-Boolean algebras (Theorem 44).
1.1.1 I Semilattice Semantics for ⊢c
In this section, we establish that the calculus ⊢c is sound and complete with respect to the class of semilattice interpretations of the language \(\mathcal {L}_{\mathrm {c}}\). As a preliminary step, we first note the following elementary fact about the calculus ⊢c:
Theorem 17
For any terms A, B of \(\mathcal {L}_{\mathrm {c}}\):
-
(i)
⊢cA ⊃ AA
-
(ii)
⊢cAB ⊃ BA
Proof
For (i): by C5, we have A ⊃ A ⊢cA ⊃ AA. Hence, by C1, ⊢cA ⊃ AA.
For (ii): by C2 and C3, we have ⊢cpAB ⊃ A and ⊢cpAB ⊃ B. Hence, by C5, ⊢cpAB ⊃ BA. □
We now introduce an algebraic semantics for the language \(\mathcal {L}_{\mathrm {c}}\):
Definition 18
An interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{\mathrm {c}}\) consists of (i) an algebraic structure \(\mathfrak {A}=\langle \mathbb {A}, \wedge \rangle \), where \(\mathbb {A}\) is a nonempty set and ∧ is a binary operation on \(\mathbb {A}\); and (ii) a function μ mapping each term of \(\mathcal {L}_{\mathrm {c}}\) to an element of \(\mathbb {A}\) such that:
A proposition A ⊃ B of \(\mathcal {L}_{\mathrm {c}}\) is satisfied in an interpretation \((\mathfrak {A},\mu )\) iff μ(A) = μ(A) ∧ μ(B). We write \((\mathfrak {A},\mu )\models A\supset B\) to indicate that \((\mathfrak {A},\mu )\) satisfies A ⊃ B.
Definition 19
An interpretation \((\langle \mathbb {A},\wedge \rangle ,\mu )\) of \(\mathcal {L}_{\mathrm {c}}\) is a semilattice interpretation if \(\langle \mathbb {A},\wedge \rangle \) is a semilattice. If Γ is a set of propositions of \(\mathcal {L}_{\mathrm {c}}\) and φ a proposition of \(\mathcal {L}_{\mathrm {c}}\), we write Γ⊧slφ to indicate that, for any semilattice interpretation \((\mathfrak {A},\mu )\): if \((\mathfrak {A},\mu )\models \psi \) for all ψ ∈ Γ, then \((\mathfrak {A},\mu )\models \varphi \).
The following completeness proof employs the standard technique introduced by Birkhoff (1935) in his proof of the algebraic completeness of equational calculi.
Theorem 20
For any set of propositions Γ of \(\mathcal {L}_{\mathrm {c}}\) and any proposition φ of \(\mathcal {L}_{\mathrm {c}}\): Γ ⊢cφ iff Γ⊧slφ.
Proof
The left-to-right direction follows straightforwardly from the fact that the principles C1–C5 (as well as the general properties of calculi stated in Definition 2) are satisfied in every semilattice interpretation.
For the right-to-left direction, let Γ be a set of propositions of \(\mathcal {L}_{\mathrm {c}}\), and let ≡ be the binary relation between terms of \(\mathcal {L}_{\mathrm {c}}\) defined by:
Clearly, if A ≡ B, then B ≡ A. Also, by C1, we have A ≡ A. By C4, we have: if A ≡ B and B ≡ C, then A ≡ C. Hence, ≡ is an equivalence relation on the set of all terms. Moreover, by Theorem 4, we have: if A ≡ B and C ≡ D, then AC ≡ BD. Thus, ≡ is a congruence relation on the algebra of terms formed by the operation of composition.
Now, let μ be the function mapping each term to its equivalence class under ≡, and let \(\mathbb {T}\) be the set \(\{\mu (A): A\ \text{is}\\text{a}\\text{term}\\text{of}\ \mathcal {L}_{\mathrm {c}}\}\). Since ≡ is a congruence relation with respect to the operation of composition, there is a binary operation ∧ on \(\mathbb {T}\) such that, for any terms A and B:
This equation implies:
In other words, the operation ∧ is associative. Now, by C2 and Theorem 17.i, we have ⊢cAA ⊃ A and ⊢cA ⊃ AA. It follows that μ(AA) = μ(A). Hence, ∧ is idempotent. Moreover, by Theorem 17.ii, we have ⊢cAB ⊃ BA and ⊢cBA ⊃ AB. It follows that μ(AB) = μ(BA). Hence, ∧ is commutative. All told, then, ∧ is an idempotent, associative, commutative operation on \(\mathbb {T}\). Hence, \(\mathfrak {T}=\langle \mathbb {T},\wedge \rangle \) is a semilattice, and \((\mathfrak {T},\mu )\) is a semilattice interpretation.
We now show that:
First, suppose that \((\mathfrak {T},\mu )\models A\supset B\). Then, μ(A) = μ(A) ∧ μ(B) = μ(AB), i.e., A ≡ AB. This implies that Γ ⊢cA ⊃ AB, and so, since ⊢cAB ⊃ B, it follows, by C4, that Γ ⊢cA ⊃ B. Next, suppose that Γ ⊢cA ⊃ B. Then, since ⊢cA ⊃ A, by C5, we have Γ ⊢cA ⊃ AB. But, since, by C2, ⊢cAB ⊃ A, it follows that A ≡ AB, i.e., μ(A) = μ(AB) = μ(A) ∧ μ(B). But this means that \((\mathfrak {T}, \mu )\models A\supset B\).
Now, suppose Γ⊬cφ. Then, \((\mathfrak {T},\mu )\not \models \varphi \). But since Γ ⊢cψ for all ψ ∈ Γ, it follows that \((\mathfrak {T},\mu )\models \psi \) for all ψ ∈ Γ. Hence, since \((\mathfrak {T},\mu )\) is a semilattice interpretation, Γ⊭slφ. □
1.1.2 I Boolean Semantics for ⊢cp
In this section, we establish that the calculus ⊢cp is sound and complete with respect to the class of Boolean interpretations of the language \(\mathcal {L}_{\mathrm {cp}}\). As a preliminary step, we first note a few elementary facts about the calculus ⊢cp.
Theorem 21
For any terms A, B of \(\mathcal {L}_{\mathrm {cp}}\):
-
(i)
\(A\supset \overline {B} \vdash _{\mathrm {cp}} AB\supset \overline {AB}\)
-
(ii)
\(A\supset \overline {B} \vdash _{\mathrm {cp}} B\supset \overline {A}\)
-
(iii)
\(\vdash _{\mathrm {cp}} A\supset \overline {\overline {A}}\)
-
(iv)
\(A\supset B \dashv \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\)
-
(v)
\(A\supset \overline {A} \vdash _{\mathrm {cp}} A\supset B\)
-
(vi)
\(\vdash _{\mathrm {cp}} A\overline {A} \supset B\)
Proof
For (i): by C3 and CP1, we have \(\vdash _{\mathrm {cp}} \overline {B} \supset \overline {AB}\). Also, by C2 and C4, \( A \supset \overline {B} \vdash _{\mathrm {cp}} AB \supset \overline {B}\). Hence, by C4, \(A\supset \overline {B} \vdash _{\mathrm {cp}} AB\supset \overline {AB}\).
For (ii): by Theorem 17.ii and CP1, we have \(\vdash _{\mathrm {cp}} \overline {AB}\supset \overline {BA}\). Now, by (i) above and C4, we have \(A\supset \overline {B} \vdash _{\mathrm {cp}} BA\supset \overline {BA}\). Hence, by CP3, \(A\supset \overline {B} \vdash _{\mathrm {cp}} B\supset \overline {A}\).
For (iii): by (ii) above, we have \(\overline {A}\supset \overline {A} \vdash _{\mathrm {cp}} A\supset \overline {\overline {A}}\). Hence, by C1, \(\vdash _{\mathrm {cp}} A \supset \overline {\overline {A}}\).
For (iv): by CP3 and (i) above, \(A\supset \overline {\overline {B}} \dashv \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\). But by (iii) above, CP2, and C4, we have \(A\supset \overline {\overline {B}} \dashv \vdash _{\mathrm {cp}} A\supset B\). Hence, \(A\supset B \dashv \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\).
For (v): by C2 and CP1, we have both \( \vdash _{\mathrm {cp}} A\overline {B}\supset A\) and \( \vdash _{\mathrm {cp}} \overline {A}\supset \overline {A\overline {B}}\). So, by C4, \(A\supset \overline {A} \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\). Hence, by (iv) above, \(A\supset \overline {A} \vdash _{\mathrm {cp}} A\supset B\).
For (vi): by (iv) above, \(A\supset A \vdash _{\mathrm {cp}} A\overline {A}\supset \overline {A\overline {A}}\). So, by C1, \(\vdash _{\mathrm {cp}} A\overline {A}\supset \overline {A\overline {A}}\). Hence, by (v) above, \(\vdash _{\mathrm {cp}} A\overline {A} \supset B\). □
Theorem 22
For any terms A, B, C of \(\mathcal {L}_{\mathrm {cp}}\):
-
(i)
\(A\overline {B}\supset C\overline {C}, C\overline {C}\supset A\overline {B}\vdash _{\mathrm {cp}} A\supset B\)
-
(ii)
\(A\supset B \vdash _{\mathrm {cp}} A\overline {B}\supset C\overline {C}\)
-
(iii)
\(A\supset B \vdash _{\mathrm {cp}} C\overline {C}\supset A\overline {B}\)
Proof
For (i): by Theorem 21.vi, we have \(\vdash _{\mathrm {cp}} C\overline {C}\supset \overline {A\overline {B}}\). So, by C4, \(A\overline {B}\supset C\overline {C} \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\). But, by Theorem 21.iv, this implies \(A\overline {B}\supset C\overline {C} \vdash _{\mathrm {cp}} A\supset B\). Hence, \(A\overline {B}\supset C\overline {C}, C\overline {C}\supset A\overline {B}\vdash _{\mathrm {cp}} A\supset B\).
For (ii): by Theorem 21.iv, we have \(A\supset B \vdash _{\mathrm {cp}} A\overline {B}\supset \overline {A\overline {B}}\). Hence, by Theorem 21.v, \(A\supset B \vdash _{\mathrm {cp}} A\overline {B}\supset C\overline {C}\).
Lastly, (iii) follows by Theorem 21.vi. □
We now introduce an algebraic semantics for the language \(\mathcal {L}_{\mathrm {cp}}\):
Definition 23
An interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{\mathrm {cp}}\) consists of (i) an algebraic structure \(\mathfrak {A}=\langle \mathbb {A}, \wedge , '\rangle \), where \(\mathbb {A}\) is a nonempty set, ∧ is a binary operation on \(\mathbb {A}\), and ′ is a unary operation on \(\mathbb {A}\); and (ii) a function μ mapping each term of \(\mathcal {L}_{\mathrm {cp}}\) to an element of \(\mathbb {A}\) such that:
A proposition A ⊃ B of \(\mathcal {L}_{\mathrm {cp}}\) is satisfied in an interpretation \((\mathfrak {A},\mu )\) iff μ(A) = μ(A) ∧ μ(B). We write \((\mathfrak {A},\mu )\models A\supset B\) to indicate that \((\mathfrak {A},\mu )\) satisfies A ⊃ B.
Definition 24
An interpretation \((\langle \mathbb {A}, \wedge , '\rangle ,\mu )\) of \(\mathcal {L}_{\mathrm {cp}}\) is a Boolean interpretation if \(\langle \mathbb {A},\wedge , '\rangle \) is a Boolean algebra. If Γ is a set of propositions of \(\mathcal {L}_{\mathrm {cp}}\) and φ a proposition of \(\mathcal {L}_{\mathrm {cp}}\), we write Γ⊧baφ to indicate that, for any Boolean interpretation \((\mathfrak {A},\mu )\): if \((\mathfrak {A},\mu )\models \psi \) for all ψ ∈ Γ, then \((\mathfrak {A},\mu )\models \varphi \).
The following completeness proof relies on a concise axiomatization of the theory of Boolean algebras discovered by Byrne (1946). In the language \(\mathcal {L}_{\mathrm {cp}}\), the main principle in this axiomatization is given by Theorem 22.
Theorem 25
For any set of propositions Γ of \(\mathcal {L}_{\mathrm {cp}}\) and any proposition φ of \(\mathcal {L}_{\mathrm {cp}}\): Γ ⊢cpφ iff Γ⊧baφ.
Proof
The left-to-right direction follows straightforwardly from the fact that the principles C1–C5 and CP1–CP3 are satisfied in every Boolean interpretation.
For the right-to-left direction, let Γ be a set of propositions of \(\mathcal {L}_{\mathrm {cp}}\), and let ≡ be the binary relation between terms of \(\mathcal {L}_{\mathrm {cp}}\) defined by:
Following the reasoning in the proof of Theorem 20, ≡ is an equivalence relation on the set of terms of \(\mathcal {L}_{\mathrm {cp}}\). Moreover, by Theorem 4 and CP1, ≡ is a congruence relation on the algebra of terms formed by the operations of composition and privation.
Now, let μ be the function mapping each term to its equivalence class under ≡, and let \(\mathbb {T}\) be the set \(\{\mu (A): A\ \text{is}\\text{a}\\text{term}\\text{of}\ \mathcal {L}_{\mathrm {cp}}\}\). Since ≡ is a congruence relation with respect to the operations of composition and privation, there is a binary operation ∧ on \(\mathbb {T}\) and a unary operation ′ on \(\mathbb {T}\) such that, for any terms A and B:
The operation ∧ is associative and commutative (see the proof of Theorem 20). Moreover, by Theorem 22, we have for any terms A, B, C of \(\mathcal {L}_{\mathrm {cp}}\):
Byrne (1946: 269–271) has shown that this latter condition, in conjunction with the associativity and commutativity of ∧, implies that \(\mathfrak {T}=\langle \mathbb {T},\wedge ,'\rangle \) is a Boolean algebra. Hence \((\mathfrak {T},\mu )\) is a Boolean interpretation.
Following the reasoning in the proof of Theorem 20, we have:
Now, suppose Γ⊬cpφ. Then, \((\mathfrak {T},\mu )\not \models \varphi \). But since Γ ⊢cpψ for all ψ ∈ Γ, it follows that \((\mathfrak {T},\mu )\models \psi \) for all ψ ∈ Γ. Hence, since \((\mathfrak {T},\mu )\) is a Boolean interpretation, Γ⊭baφ. □
1.1.3 I Auto-Boolean Semantics for ⊢
In this section, we establish that the containment calculus ⊢ is sound and complete with respect to the class of auto-Boolean interpretations of the language \(\mathcal {L}_{\supset }\). The proof of completeness will rely on the auto-Boolean completeness of the coincidence calculus developed by Leibniz’s in the Generales inquisitiones. We begin by establishing some preliminary facts about the containment calculus ⊢.
Definition 26
For any term A of \(\mathcal {L}_{\supset }\), we write  for the proposition \(A\supset \overline {A}\).
for the proposition \(A\supset \overline {A}\).
Theorem 27
For any propositions φ, ψ, χ of \(\mathcal {L}_{\supset }\):
-
(i)
If φ, ψ ⊢ χ, then \(\varphi , \, \mathbf {F}(\ulcorner {\chi }\urcorner ) \, \vdash \, \mathbf {F}(\ulcorner {\psi }\urcorner )\)
-
(ii)
φ ⊢ ψ iff \(\vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\psi }\urcorner \)
-
(iii)
If φ ⊢ ψ, then \( \mathbf {F}(\ulcorner {\psi }\urcorner ) \, \vdash \, \mathbf {F}(\ulcorner {\varphi }\urcorner )\)
Proof
For (i): suppose that φ, ψ ⊢ χ. By PT3, we have \(\varphi \vdash \ulcorner {\psi }\urcorner \supset \ulcorner {\chi }\urcorner \). Hence, by CP1, \(\varphi \vdash \overline {\ulcorner {\chi }\urcorner }\supset \overline {\ulcorner {\psi }\urcorner }\). By C4, PT1, and PT2, it follows that \(\varphi \vdash \ulcorner {\mathbf {F}(\ulcorner {\chi }\urcorner )}\supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )}\). Hence, by PT3, \(\varphi , \mathbf {F}(\ulcorner {\chi }\urcorner ) \vdash \mathbf {F}(\ulcorner {\psi }\urcorner )\).
For (ii): by PT3, A ⊃ A, φ ⊢ ψ iff \(A\supset A\vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\psi }\urcorner \). Hence, by C1, φ ⊢ ψ iff \( \vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\psi }\urcorner \).
For (iii): suppose that φ ⊢ ψ. Then, A ⊃ A, φ ⊢ ψ. By (i) above, we have \(A \supset A, \mathbf {F}(\ulcorner {\psi }\urcorner ) \vdash \mathbf {F}(\ulcorner {\varphi }\urcorner )\). Hence, by C1, \(\mathbf {F}(\ulcorner {\psi }\urcorner ) \vdash \mathbf {F}(\ulcorner {\varphi }\urcorner )\). □
Theorem 28
For any proposition φ of \(\mathcal {L}_{\supset }\) :
-
(i)
\( \mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}) \,\vdash \, \varphi \)
-
(ii)
\( \varphi \,\vdash \, \mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})\)
Proof
For (i): by PT2, we have \( \vdash \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})} \supset \overline {\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}}\). Moreover, by PT1 and CP1, we have \(\vdash \overline {\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}} \supset \overline {\overline {\ulcorner {\varphi }\urcorner }}\). Hence, by C4, \( \vdash \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})} \supset \overline {\overline {\ulcorner {\varphi }\urcorner }}\). By CP2 and C4, it follows that \( \vdash \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})} \supset \ulcorner {\varphi }\urcorner \). Hence, by Theorem 27.ii, \(\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}) \vdash \varphi \).
For (ii): by PT1, we have \( \vdash \overline {\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}} \supset \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})}\). Moreover, by PT2 and CP1, we have \(\vdash \overline {\overline {\ulcorner {\varphi }\urcorner }} \supset \overline {\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}}\). Hence, by C4, \( \vdash \overline {\overline {\ulcorner {\varphi }\urcorner }} \supset \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})}\). By Theorem 21.iii and C4, it follows that \( \vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )})} \). Hence, by Theorem 27.ii, \(\varphi \vdash \mathbf {F}(\ulcorner {\mathbf {F}(\ulcorner {\varphi }\urcorner )}) \). □
Theorem 29
For any propositions φ, ψ of \(\mathcal {L}_{\supset }\):
-
(i)
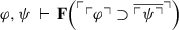
-
(ii)
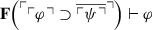
-
(iii)
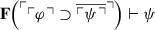
Proof
For (i): since \(\ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )} \vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )}\), by PT3 we have \(\varphi , \ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )} \vdash \mathbf {F}(\ulcorner {\psi }\urcorner )\). By C4 and PT1, it follows that \(\varphi , \ulcorner {\varphi }\urcorner \supset \overline {\ulcorner {\psi }\urcorner } \vdash \mathbf {F}(\ulcorner {\psi }\urcorner )\). Hence, by Theorem 27.i,  . The desired result follows by Theorem 28.ii.
. The desired result follows by Theorem 28.ii.
For (ii): since φ, ψ ⊢ φ, by Theorem 27.i we have \(\varphi , \mathbf {F}(\ulcorner {\varphi }\urcorner ) \vdash \mathbf {F}(\ulcorner {\psi }\urcorner )\). By PT3, it follows that \(\mathbf {F}(\ulcorner {\varphi }\urcorner ) \vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )}\). Hence, by PT2 and C4, \(\mathbf {F}(\ulcorner {\varphi }\urcorner ) \vdash \ulcorner {\varphi }\urcorner \supset \overline {\ulcorner {\psi }\urcorner }\). By Theorem 27.iii, it follows that  . The desired result follows by Theorem 28.i.
. The desired result follows by Theorem 28.i.
For (iii): since \(\varphi , \mathbf {F}(\ulcorner {\psi }\urcorner ) \vdash \mathbf {F}(\ulcorner {\psi }\urcorner )\), by PT3 we have \(\mathbf {F}(\ulcorner {\psi }\urcorner ) \vdash \ulcorner {\varphi }\urcorner \supset \ulcorner {\mathbf {F}(\ulcorner {\psi }\urcorner )}\). Hence, by C4 and PT2, \(\mathbf {F}(\ulcorner {\psi }\urcorner ) \vdash \ulcorner {\varphi }\urcorner \supset \overline {\ulcorner {\psi }\urcorner }\). By Theorem 27.iii, it follows that  . The desired result follows by Theorem 28.i. □
. The desired result follows by Theorem 28.i. □
Definition 30
For any terms A, B of \(\mathcal {L}_{\supset }\), we write A ≈ B for the proposition:

Theorem 31
For any terms A, B of \(\mathcal {L}_{\supset }\):
-
(i)
A ⊃ B ⊣⊢ A ≈ AB
-
(ii)
⊢ AA ≈ A
-
(iii)
⊢ AB ≈ BA
-
(iv)
\(\vdash \overline {\overline {A}}\approx A\)
Proof
For (i): by C2, we have ⊢ AB ⊃ A, and so A ⊃ B ⊢ AB ⊃ A. Moreover, by C1 and C5, we have A ⊃ B ⊢ A ⊃ AB. Hence, by Theorem 29.i, A ⊃ B ⊢ A ≈ AB. For the converse, by Theorem 29.ii, we have A ≈ AB ⊢ A ⊃ AB. Hence, by C3 and C4, A ≈ AB ⊢ A ⊃ B.
For (ii): by C2, we have ⊢ AA ⊃ A. Moreover, by Theorem 17.i, we have ⊢ A ⊃ AA. Hence, by Theorem 29.i, ⊢ AA ≈ A.
For (iii): by Theorem 17.ii, we have both ⊢ AB ⊃ BA and ⊢ BA ⊃ AB. Hence, by Theorem 29.i, ⊢ AB ≈ BA.
For (iv): by CP2, we have \(\vdash \overline {\overline {A}}\supset A\). Moreover, by Theorem 21.iii, we have \(\vdash A\supset \overline {\overline {A}}\). Hence, by Theorem 29.i, \(\vdash \overline {\overline {A}}\approx A\). □
In the remainder of this section, we establish that the calculus ⊢ is complete with respect to the class of auto-Boolean algebras. This completeness proof will rely on the auto-Boolean completeness of the coincidence calculus developed by Leibniz in the Generales inquisitiones. The crucial step in the proof will be to show that all the theorems of the latter calculus can be reproduced in the containment calculus ⊢. To this end, we first specify the language \(\mathcal {L}_{=}\) of Leibniz’s coincidence calculus:
Definition 32
The terms and propositions of the language \(\mathcal {L}_{=}\) are defined as follows:
-
(1)
Every simple term of the language \(\mathcal {L}_{\supset }\) is a term.
-
(2)
If A and B are terms, then AB is a term.
-
(3)
If A is a term, then \(\overline {A}\) is a term.
-
(4)
If A and B are terms, then A = B is a proposition.
-
(5)
If A = B is a proposition, then \(\ulcorner {A=B}\urcorner \) is a term.
The following two definitions describe how the terms and propositions of \(\mathcal {L}_{\supset }\) can be translated into the language \(\mathcal {L}_{=}\) and vice versa:
Definition 33
The function σ maps every term or proposition of \(\mathcal {L}_{\supset }\) to a term or proposition of \(\mathcal {L}_{=}\) as follows:
-
(1)
If A is a simple term of \(\mathcal {L}_{\supset }\), then σ(A) is the term A.
-
(2)
σ(AB) is the term σ(A)σ(B).
-
(3)
\(\sigma (\overline {A})\) is the term \(\overline {\sigma (A)}\).
-
(4)
σ(A ⊃ B) is the proposition σ(A) = σ(A)σ(B)
-
(5)
σ(⌜φ⌝) is the term ⌜σ(φ)⌝.
If Γ is a set of propositions of \(\mathcal {L}_{\supset }\), we write σ( Γ) for the set {σ(φ) : φ ∈ Γ}.
Definition 34
The function τ maps every term or proposition of \(\mathcal {L}_{=}\) to a term or proposition of \(\mathcal {L}_{\supset }\) as follows:
-
(1)
If A is a simple term of \(\mathcal {L}_{\supset }\), then τ(A) is the term A.
-
(2)
τ(AB) is the term τ(A)τ(B).
-
(3)
\(\tau (\overline {A})\) is the term \(\overline {\tau (A)}\).
-
(4)
τ(A = B) is the proposition τ(A) ≈ τ(B)
-
(5)
τ(⌜φ⌝) is the term ⌜τ(φ)⌝.
If Γ is a set of propositions of \(\mathcal {L}_{=}\), we write τ( Γ) for the set {τ(φ) : φ ∈ Γ}.
Theorem 35
For any term A and any proposition φ of \(\mathcal {L}_{\supset }\) :
-
(i)
⊢ A ⊃ τ(σ(A)) and ⊢ τ(σ(A)) ⊃ A
-
(ii)
φ ⊣⊢ τ(σ(φ))
Proof
The proof proceeds by mutual induction on the structure of the terms and propositions of \(\mathcal {L}_{\supset }\) (see Definition 13). First, suppose that A is a simple term of \(\mathcal {L}_{\supset }\). Then τ(σ(A)) just is the term A, and so the claim follows by C1.
Next, suppose that the claim holds for the terms A and B. By Theorem 4, we have:
But since τ(σ(A))τ(σ(B)) is the term τ(σ(AB)), the claim holds for the term AB. Moreover, by CP1, we have:
But since \(\overline {\tau (\sigma (A))}\) is the term \(\tau (\sigma (\overline {A}))\), the claim holds for the term \(\overline {A}\).
Next, given that the claim holds for the terms A and B, it follows by the rule of substitution for containment established in Theorem 15 that:
Hence, by Theorem 31.i, we have:
But since τ(σ(A)) ≈ τ(σ(A))τ(σ(B)) is the proposition τ(σ(A ⊃ B)), the claim holds for the proposition A ⊃ B.
Finally, suppose that the claim holds for the proposition φ. By Theorem 27.ii, we have:
But since ⌜τ(σ(φ))⌝ is the term \(\tau (\sigma (\ulcorner {\varphi }\urcorner ))\), the claim holds for the term \(\ulcorner {\varphi }\urcorner \). This completes the induction. □
We now introduce the coincidence calculus, \(\Vdash \), developed by Leibniz in the Generales inquisitiones (as reconstructed in Malink and Vasudevan 2016: 696–706):
Definition 36
The calculus \(\Vdash \) is the smallest calculus in the language \(\mathcal {L}_{=}\) such that:
- (P1):
-
\(\Vdash AA=A\)
- (P2):
-
\(\Vdash AB=BA\)
- (P3):
-
\(\Vdash \overline {\overline {A}}=A\)
- (P4):
-
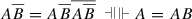
- (P5):
-
\(\Vdash \overline {\ulcorner {\varphi }\urcorner } = \ulcorner {\ulcorner {\varphi }\urcorner =\ulcorner {\varphi }\urcorner \overline {\ulcorner {\varphi }\urcorner }}\)
- (P6):
-
\(\varphi \Vdash \psi \) iff \(\Vdash \ulcorner {\varphi }\urcorner =\ulcorner {\varphi }\urcorner \ulcorner {\psi }\urcorner \)
- (P7):
-
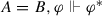 , where
, where 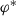 is the result of substituting B for an
is the result of substituting B for anoccurrence of A, or vice versa, in φ.
The following result states that all theorems of the coincidence calculus \(\Vdash \) can be reproduced under the translation τ in the containment calculus ⊢:
Theorem 37
For any set of propositions Γ of \(\mathcal {L}_{=}\) and any proposition φ of \(\mathcal {L}_{=}\): if \(\Gamma \Vdash \varphi \), then τ( Γ) ⊢ τ(φ).
Proof
The proof proceeds by induction on the definition of the coincidence calculus \(\Vdash \) (Definition 36). For P1–P6, it suffices to show that for any terms A, B of \(\mathcal {L}_{\supset }\) and any propositions φ, ψ of \(\mathcal {L}_{\supset }\):
-
(i)
⊢ AA ≈ A
-
(ii)
⊢ AB ≈ BA
-
(iii)
\(\vdash \overline {\overline {A}}\approx A\)
-
(iv)
\(A\overline {B}\approx A\overline {B}\overline {A\overline {B}}\dashv \vdash A\approx AB\)
-
(v)
\(\vdash \overline {\ulcorner {\varphi }\urcorner } \approx \ulcorner {\ulcorner {\varphi }\urcorner \approx \ulcorner {\varphi }\urcorner \overline {\ulcorner {\varphi }\urcorner }}\)
-
(vi)
φ ⊢ ψ iff \(\vdash \ulcorner {\varphi }\urcorner \approx \ulcorner {\varphi }\urcorner \ulcorner {\psi }\urcorner \)
Claims (i)–(iii) are stated in Theorem 31.ii–iv. Claim (iv) follows by Theorems 21.iv and 31.i. For claim (v), by Theorems 31.i and 27.ii, we have:
Hence, by PT1, PT2, and C4, we have:
Claim (v) then follows by Theorem 29.i.
Claim (vi) follows by Theorems 27.ii and 31.i.
Finally, for P7 we must show that, for any terms A, B of \(\mathcal {L}_{=}\) and any proposition φ of \(\mathcal {L}_{=}\): if  is the result of substituting B for an occurrence of A, or vice versa, in φ, then
is the result of substituting B for an occurrence of A, or vice versa, in φ, then  . To see this, we first note that, given Definition 34, if
. To see this, we first note that, given Definition 34, if  is the result of substituting A for an occurrence of B, or vice versa, in φ, then
is the result of substituting A for an occurrence of B, or vice versa, in φ, then  is the result of substituting τ(A) for one or more occurrences of τ(B), or vice versa, in τ(φ). Moreover, it follows by Theorems 15 and 29.ii–iii that, if
is the result of substituting τ(A) for one or more occurrences of τ(B), or vice versa, in τ(φ). Moreover, it follows by Theorems 15 and 29.ii–iii that, if  is the result of substituting τ(A) for one or more occurrences of τ(B), or vice versa, in τ(φ), then
is the result of substituting τ(A) for one or more occurrences of τ(B), or vice versa, in τ(φ), then  . This completes the induction. □
. This completes the induction. □
We now introduce an algebraic semantics for the language \(\mathcal {L}_{=}\):
Definition 38
An interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{=}\) consists of (i) an algebraic structure \(\mathfrak {A}=\langle \mathbb {A}, \wedge , '\rangle \), where \(\mathbb {A}\) is a nonempty set, ∧ is a binary operation on \(\mathbb {A}\), and ′ is a unary operation on \(\mathbb {A}\); and (ii) a function μ mapping each term of \(\mathcal {L}_{=}\) to an element of \(\mathbb {A}\) such that:
A proposition A = B of \(\mathcal {L}_{=}\) is satisfied in an interpretation \((\mathfrak {A},\mu )\) iff μ(A) = μ(B). We write  to indicate that \((\mathfrak {A},\mu )\) satisfies A = B.
to indicate that \((\mathfrak {A},\mu )\) satisfies A = B.
Definition 39
An interpretation \((\langle \mathbb {A}, \wedge , '\rangle , \mu )\) of \(\mathcal {L}_{=}\) is an auto-Boolean interpretation iff \(\langle \mathbb {A}, \wedge , '\rangle \) is a Boolean algebra such that, for any terms A, B of \(\mathcal {L}_{=}\):
Here, 1 and 0 are the top and bottom elements of the Boolean algebra \(\langle \mathbb {A}, \wedge , '\rangle \), respectively. If Γ is a set of propositions of \(\mathcal {L}_{=}\) and φ a proposition of \(\mathcal {L}_{=}\), we write  to indicate that, for any auto-Boolean interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{=}\): if
to indicate that, for any auto-Boolean interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{=}\): if  for all ψ ∈ Γ, then
for all ψ ∈ Γ, then  .
.
The following theorem asserts that the coincidence calculus \(\Vdash \) is complete with respect to the class of auto-Boolean interpretations of \(\mathcal {L}_{=}\):
Theorem 40
For any set of propositions Γ of \(\mathcal {L}_{=}\) and any proposition φ of \(\mathcal {L}_{=}\): if  , then \(\Gamma \Vdash \varphi \).
, then \(\Gamma \Vdash \varphi \).
The proof of this completeness theorem is given in Malink and Vasudevan 2016: 744–8 (Theorem 4.94).
With this completeness theorem for the coincidence calculus \(\Vdash \) in hand, we are now in a position to establish the auto-Boolean completeness of the cointainment calculus ⊢. To this end, we first introduce an algebraic semantics for the language \(\mathcal {L}_{\supset }\):
Definition 41
An interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{\supset }\) consists of (i) an algebraic structure \(\mathfrak {A}=\langle \mathbb {A}, \wedge , '\rangle \), where \(\mathbb {A}\) is a nonempty set, ∧ is a binary operation on \(\mathbb {A}\), and ′ is a unary operation on \(\mathbb {A}\); and (ii) a function μ mapping each term of \(\mathcal {L}_{\supset }\) to an element of \(\mathbb {A}\) such that:
A proposition A ⊃ B of \(\mathcal {L}_{\supset }\) is satisfied in an interpretation \((\mathfrak {A},\mu )\) iff μ(A) = μ(A) ∧ μ(B). We write \((\mathfrak {A},\mu )\models A\supset B\) to indicate that \((\mathfrak {A},\mu )\) satisfies A ⊃ B.
Definition 42
An interpretation \((\langle \mathbb {A}, \wedge , '\rangle , \mu )\) of \(\mathcal {L}_{\supset }\) is an auto-Boolean interpretation iff \(\langle \mathbb {A}, \wedge , '\rangle \) is a Boolean algebra such that, for any terms A, B of \(\mathcal {L}_{\supset }\):
Here, 1 and 0 are the top and bottom elements of the Boolean algebra \(\langle \mathbb {A}, \wedge , '\rangle \), respectively. If Γ is a set of propositions of \(\mathcal {L}_{\supset }\) and φ a proposition of \(\mathcal {L}_{\supset }\), we write Γ⊧φ to indicate that, for any auto-Boolean interpretation \((\mathfrak {A},\mu )\) of \(\mathcal {L}_{\supset }\): if \((\mathfrak {A},\mu )\models \psi \) for all ψ ∈ Γ, then \((\mathfrak {A},\mu )\models \varphi \).
Theorem 43
For any set of propositions Γ of \(\mathcal {L}_{\supset }\) and any proposition φ of \(\mathcal {L}_{\supset }\): if Γ⊧φ, then  .
.
Proof
Let \((\mathfrak {A},\mu )=(\langle \mathbb {A}, \wedge , '\rangle , \mu )\) be an auto-Boolean interpretation of \(\mathcal {L}_{=}\), and let  be the function mapping each term of \(\mathcal {L}_{\supset }\) to an element of \(\mathbb {A}\) defined by:
be the function mapping each term of \(\mathcal {L}_{\supset }\) to an element of \(\mathbb {A}\) defined by:
We then have:
Hence, by Definition 42,  is an auto-Boolean interpretation of \(\mathcal {L}_{\supset }\).
is an auto-Boolean interpretation of \(\mathcal {L}_{\supset }\).
Now, suppose that Γ⊧φ and that  for all ψ ∈ σ( Γ). By Definition 41 and the definition of
for all ψ ∈ σ( Γ). By Definition 41 and the definition of  , we have for any proposition ψ of \(\mathcal {L}_{\supset }\):
, we have for any proposition ψ of \(\mathcal {L}_{\supset }\):  iff
iff  . Hence,
. Hence,  for all ψ ∈ Γ. But since
for all ψ ∈ Γ. But since  is an auto-Boolean interpretation of \(\mathcal {L}_{\supset }\), it follows that
is an auto-Boolean interpretation of \(\mathcal {L}_{\supset }\), it follows that  . Thus, by the above biconditional,
. Thus, by the above biconditional,  . So, if
. So, if  for all ψ ∈ σ( Γ), then
for all ψ ∈ σ( Γ), then  . But since \((\mathfrak {A},\mu )\) was an arbitrary auto-Boolean interpretation of \(\mathcal {L}_{=}\), this means that
. But since \((\mathfrak {A},\mu )\) was an arbitrary auto-Boolean interpretation of \(\mathcal {L}_{=}\), this means that  . □
. □
The following theorem asserts that the containment calculus ⊢ is sound and complete with respect to the class of auto-Boolean interpretations of \(\mathcal {L}_{\supset }\):
Theorem 44
For any set of propositions Γ of \(\mathcal {L}_{\supset }\) and any proposition φ of \(\mathcal {L}_{\supset }\): Γ ⊢ φ iff Γ⊧φ.
Proof
The left-to-right direction follows straightforwardly from the fact that the principles C1–C5, CP1–CP3, and PT1–PT3 are satisfied in every auto-Boolean interpretation.
For the right-to-left direction, suppose that Γ⊧φ. Then, by Theorem 43,  . By Theorem 40, \(\sigma (\Gamma )\Vdash \sigma (\varphi )\). By Theorem 37, τ(σ( Γ)) ⊢ τ(σ(φ)). Hence, by Theorem 35.ii, it follows that Γ ⊢ φ. □
. By Theorem 40, \(\sigma (\Gamma )\Vdash \sigma (\varphi )\). By Theorem 37, τ(σ( Γ)) ⊢ τ(σ(φ)). Hence, by Theorem 35.ii, it follows that Γ ⊢ φ. □
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Malink, M., Vasudevan, A. (2019). Leibniz on the Logic of Conceptual Containment and Coincidence. In: De Risi, V. (eds) Leibniz and the Structure of Sciences. Boston Studies in the Philosophy and History of Science, vol 337. Springer, Cham. https://doi.org/10.1007/978-3-030-25572-5_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-25572-5_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25571-8
Online ISBN: 978-3-030-25572-5
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 , where φ is any proposition of the form C ⊃ D or C = D.
, where φ is any proposition of the form C ⊃ D or C = D.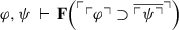
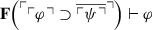
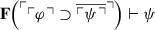
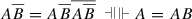
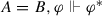 , where
, where 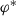 is the result of substituting B for an
is the result of substituting B for an