Keywords

1 Introduction

In the last decade, large-scale natural disasters have occurred frequently. Such natural disasters pose serious threats to the sustainable development of society, economy, and ecology. A large number of people are impacted significantly and a lot of assets are damaged severely. Upon these disasters, relief centers should be determined and emergency commodity should be distributed to these relief centers to provide basic life support [1,2,3]. However, because the initial commodity distribution may be unbalanced due to the incomplete information and uncertain environment, each relief center may have a surplus or a shortage. In such a situation, the surplus should be redelivered to other unmet relief centers to make the efficient use of the commodity. In the transportation process to rebalance the commodity, traffic congestion is considered, because large-scale disasters usually trigger huge demand and service in the disaster area, which makes the mobile network operators no longer able to provide demand and service sufficiently. Hence, tasks to rebalance the commodity over the transportation network with traffic congestion are very difficult to accomplish under demand and supply uncertainties. Against the backdrop of difficulties, the aim of this study is to formulate this commodity rebalancing problem with stochastic elements considering traffic congestion and solve it using mathematical programming.

The rest of this paper is organized as follows. Section 2 reviews previous studies and highlights the main differences from the previous studies. Section 3 provides a problem description, a stochastic optimization model, and a solution method. Then, the application of the proposed model in a numerical instance is shown where the results are presented and discussed in Sect. 4. Finally, Sect. 5 concludes this study with contributions and further directions.

2 Literature Review

Humanitarian logistics research has attracted growing attention as human suffering and economic loss continue to increase. In the past, many studies mainly surveyed on the humanitarian logistics for disaster management. Caunhye and Nie [4] reviewed optimization models in emergency logistics, which were divided into the following parts: facility location, relief distribution, casualty transportation, and other operations. Galindo and Batta [5] reviewed recent OR/MS research in disaster operations management and provided future research directions. Here, the related studies are reviewed on the commodity distribution, commodity rebalancing (also referred to as redistribution), and humanitarian logistics under the consideration of traffic congestion in disaster response. Dessouky and Ordonez [6] argued two important issues to solve facility location and vehicle routing problems that could ensure the rapid distribution of medical supplies in a logistics network. Jotshi and Gong [7] developed a robust methodology for dispatching and routing emergency vehicles in a post-disaster environment with the support of data fusion. Chen and Yu [8] applied an integer programming and a network-based partitioning to determine temporary locations for on-post EMS facilities after the disaster. Al Theeb and Murray [9] presented a mathematical programming model to deliver goods, disaster victims, and volunteer workers through a road network. Gao and Lee [10] proposed a stochastic programming model to facilitate the multi-commodity redistribution process under uncertainty. Gao and Lee [11] proposed a two-stage stochastic programming model to design a multi-modal transportation network for multi-commodity redistribution.

Traffic congestion is one of the most important factors to delay humanitarian logistics and contribute to increasing the time of delivery and the number of injuries after disasters [12]. Transportation time may also be affected by traffic congestion on the roads due to various reasons [7]. Feng and Wen [13] pointed out that the roadway systems usually got different levels of damage, and thus the roadway capacity was reduced, which caused traffic congestion after a severe earthquake. Nagurney and Flores [14] proposed a network model which consisted of multiple nongovernmental organizations who sought to supply multiple demand points with relief items post a disaster to reduce the convergence and even congestion. To estimate the traffic congestion, the travel time function suggested in the traditional Bureau of Public Roads (BPR) curve [15] provides the relationship between the link travel time and the volume of traffic on a highway network, which is shown in the following functional form:

$$ F\left( x \right) = F_{0} \cdot \left[ {1.0 + \alpha \cdot \left( {\frac{x}{C}} \right)^{\beta } } \right]. $$
(1)

where \( F\left( x \right) \) is the link travel time when the link-flow rate is \( x \), \( F_{0} \) is the free flow travel time, \( C \) is the practical link capacity, and \( \alpha \ge 0 \), \( \beta \ge 0 \) are parameters. This BPR function is widely used in the transportation planning field [16].

In spite of many studies that have been dedicated to humanitarian logistics after the disasters, few of them concern the commodity rebalancing process. To fill this research gap, this study focuses on the commodity rebalancing problem that incorporates traffic congestion. The novelty and contribution can be summarized as follows. A stochastic mixed-integer nonlinear programming model is proposed to formulate this commodity rebalancing problem, which has never been studied before. Then, a linearization method is also proposed to reformulate the nonlinear model so that it can be solved in the optimization solver CPLEX. Finally, a numerical instance is carried out and some managerial insights are obtained.

3 Problem and Methodology

3.1 Problem Statement

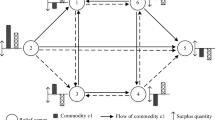
A transportation network which consists of a number of roads and relief centers is considered in this study. An initial commodity distribution has been delivered to these relief centers. Upon the disaster, the surplus commodity at some relief centers needs to be redelivered to other unmet relief centers. It is difficult to determine how much of commodity should be delivered and received at each relief center, which makes the supply and demand uncertain. In this study, a scenario-based approach is applied for uncertain elements, which are represented in terms of a number of discrete realizations of stochastic quantities. Generally, in a demand or supply relief center, there is a set of scenarios \( \varXi \). For a particular scenario \( \xi \in {\mathbb{S}} \), there is a probability of occurrence \( {\mathcal{P}}\left( \xi \right) \), such that \( {\mathcal{P}}\left( \xi \right) \ge 0 \) and \( \sum\nolimits_{{\xi \in {\mathbb{S}}}} {{\mathcal{P}}\left( \xi \right)} = 1 \). In this study, two assumptions are made: (i) each relief center is a separate unit in terms of the possible quantities of demand or supply; (ii) the available paths with background traffic-flow rates are given.

In light of the above requirements, this study develops a two-stage stochastic mixed-integer nonlinear programming model for the commodity rebalancing problem. The objective functions are to minimize the expected total weighted unmet demand in the first stage and minimize the total transportation time in the second stage.

3.2 Model Formulation

The problem is modeled using the following notations.

Sets

\( {\mathcal{S}} \) :

Set of supply relief centers, indexed by \( s \in {\mathcal{S}} \).

\( {\mathcal{D}} \) :

Set of demand relief centers, indexed by \( d \in {\mathcal{D}} \).

\( {\mathbb{S}} \) :

Set of scenarios, indexed by \( \xi \in {\mathbb{S}} \).

Parameters

\( S_{s}^{\Delta } ,S_{s}^{\nabla } \) :

The minimum and maximum supply at relief center \( s \).

\( R_{d}^{\Delta } ,R_{d}^{\nabla } \) :

The minimum and maximum demand at relief center \( d \).

\( M \) :

A big positive number.

\( W,V \) :

Commodity weight and volume.

\( CW,CV \) :

Vehicle weight and volume capacities.

\( Z^{s} ,Z^{d} \) :

Weighted values of supply relief center \( s \) and demand relief center \( d \).

\( D_{sd} \) :

Distance between relief centers \( s \) and \( d \).

\( B_{sd} \) :

Background traffic-flow rate between relief centers \( s \) and \( d \).

\( C_{sd} \) :

Practical traffic-flow rate capacity between relief centers \( s \) to \( d \).

\( T \) :

Planning period for the transportation process.

\( V \) :

Vehicle travel speed.

\( L \) :

Vehicle loading/unloading time.

\( o_{s}^{\xi } \) :

Possible supply at relief center \( s \) in scenario \( \xi \).

\( i_{d}^{\xi } \) :

Possible demand at relief center \( d \) in scenario \( \xi \).

\( p_{s}^{\xi } \) :

Probability of occurrence of \( o_{s}^{\xi } \).

\( p_{d}^{\xi } \) :

Probability of occurrence of \( i_{d}^{\xi } \).

Decision variables

\( d_{s} \) :

Outgoing quantity at relief center \( s \).

\( r_{d} \) :

Incoming quantity at relief center \( d \).

\( w_{sd} \) :

Commodity-flow from relief centers \( s \) to \( d \).

\( n_{sd} \) :

Vehicle number from relief centers \( s \) to \( d \).

The completed formulation is given as the following two-stage stochastic mixed-integer nonlinear programming model. In the first stage, the objective function is defined as follows

$$ \varPsi_{1} = \sum\nolimits_{{d \in {\mathcal{D}}}} {\sum\nolimits_{{\xi \in {\mathbb{S}}}} {p_{d}^{\xi } \cdot Z^{d} \cdot { \hbox{max} }\{ i_{d}^{\xi } - r_{d} ,0\} } } + \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{{\xi \in {\mathbb{S}}}} {p_{s}^{\xi } \cdot Z^{s} \cdot { \hbox{max} }\left\{ {d_{s} - o_{s}^{\xi } ,0} \right\}} } $$
(2)

To remove the MAX function in (2) and realize the MAX function, the following two auxiliary binary variables are introduced into the model.

(3)
(4)

Then, the commodity rebalancing problem can be formulated as a deterministic optimization model:

(5)
$$ \begin{array}{*{20}c} {{\text{s}}.{\text{t}}.} \\ {\sum\nolimits_{{s \in {\mathcal{S}}}} {d_{s} } = \sum\nolimits_{{d \in {\mathcal{D}}}} {r_{d} } ,} \\ \end{array} $$
(6)
(7)
(8)
(9)
(10)
$$ S_{s}^{\Delta } \le d_{s} \le S_{s}^{\nabla } \quad \forall \,s \in {\mathcal{S}}, $$
(11)
$$ R_{d}^{\Delta } \le r_{d} \le R_{d}^{\nabla } \quad \forall \,d \in {\mathcal{D}}, $$
(12)

where objective function (5) aims to minimize the expected total weighted unmet demand at relief centers. Constraint (6) guarantees the balance of outgoing and incoming shipments. Constraints (7)–(10) guarantee that relief centers only account for the unmet demand. Given a general positive number to \( i_{d}^{\xi } - r_{d} \), is 1, whereas is 0. Constraints (11) and (12) define the decision variables. After the first-stage decision variables are obtained, the second-stage problem can be formulated as follows.

$$ \hbox{min} \,\varPsi_{2} = \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{{d \in {\mathcal{D}}}} {T \cdot n_{sd} } } + \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{{d \in {\mathcal{D}}}} {\frac{{D_{sd} }}{V}} } \cdot \left[ {1 + \alpha \cdot \left( {\frac{{n_{sd} + B_{sd} \cdot T}}{{C_{sd} \cdot T}}} \right)^{\beta } } \right] \cdot n_{sd} $$
(13)
$$ \begin{array}{*{20}c} {{\text{s}}.{\text{t}}.} \\ {\sum\nolimits_{{d \in {\mathcal{D}}}} {w_{sd} } \le d_{s} \quad \forall \,s \in {\mathcal{S}},} \\ \end{array} $$
(14)
$$ \sum\nolimits_{{s \in {\mathcal{S}}}} {w_{sd} } \ge r_{d} \quad \forall \,d \in {\mathcal{D}}, $$
(15)
$$ \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{{d \in {\mathcal{D}}}} {w_{sd} } } = \sum\nolimits_{{d \in {\mathcal{D}}}} {\sum\nolimits_{{s \in {\mathcal{S}}}} {w_{sd} } } , $$
(16)
$$ w_{sd} \cdot W \le n_{sd} \cdot CW\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(17)
$$ w_{sd} \cdot V \le n_{sd} \cdot CV\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(18)
$$ n_{sd} \le \left( {C_{sd} - B_{sd} } \right) \cdot T\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(19)
$$ n_{sd} \ge 0\,\& \,integer\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(20)
$$ w_{sd} \ge 0\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}. $$
(21)

where the objective function (13) aims to minimize the total transportation time. Constraint (14) ensures the total outgoing shipment cannot exceed the available amount at relief center \( s \). Constraint (15) ensures that the total incoming shipment should be greater than or equal to the demand at relief center \( d \). Constraint (16) guarantees transportation balance. Constraints (17) and (18) restrict assigned vehicles should be able to deliver the commodity by satisfying both weight and volume capacities. Constraint (19) ensures that assigned vehicles cannot exceed the route capacity. Constraints (20) and (21) are nonnegative constraints of variables.

3.3 Solution Method

The second-stage objective function is nonlinear when the BPR function is considered. To linearize the second-stage objective function, two more auxiliary parameters are introduced in this study. The first one is the maximum units of the commodity in one vehicle, which is represented as \( {\text{G}} = { \hbox{min} }\left( {\frac{CW}{W},\frac{CV}{V}} \right) \). The other one is the number of vehicles \( x \) from relief centers \( s \) to \( d \), which is represented as \( n_{sd}^{x} \). Because the vehicle number must be an integer, the discrete solution space can be built. The consecutive integer numbers are used to represent the potential solution.

$$ n_{sd}^{x} \in \left\{ {0,1,2 \ldots ,x, \ldots ,\hbox{min} \left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]} \right\}\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}. $$
(22)

And an auxiliary binary variable is used to represent the second-stage decision variables.

$$ \varphi_{sd}^{x} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,n_{sd}^{x} \,{\text{vehicles}}\,{\text{are}}\,{\text{used}}\,{\text{from}}\,{\text{relief}}\,{\text{centers}}\,s\,{\text{to}}\,d.} \hfill \\ 0 \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right. $$
(23)

Then, the BPR function can be rewritten as follows.

$$ \psi \left( {n_{sd}^{x} } \right) = \left[ {1 + \alpha \cdot \left( {\frac{{n_{sd}^{x} + B_{sd} \cdot T}}{{C_{sd} \cdot T}}} \right)^{\beta } } \right] \cdot n_{sd}^{x} \quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}. $$
(24)

With the new BPR function, the second-stage model can be rewritten as follows.

$$ \text{Min}\,\varPsi_{2} = \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{{d \in {\mathcal{D}}}} {\sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}}, \frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {\left[ {{\text{T}} \cdot n_{sd}^{x} + \frac{{D_{sd} }}{V} \cdot \psi \left( {n_{sd}^{x} } \right)} \right] \cdot \varphi_{sd}^{x} ,} } } $$
(25)
$$ \begin{array}{c} {\text{s}}.{\text{t}}.\\ \sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {n_{sd}^{x} \cdot \varphi_{sd}^{x} \le \hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}},} \hfill \\ \end{array} $$
(26)
$$ \sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {n_{sd}^{x} \cdot \varphi_{sd}^{x} } \le \left( {C_{sd} - B_{sd} } \right) \cdot T\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(27)
$$ \sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {\varphi_{sd}^{x} } = 1\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}, $$
(28)
$$ \sum\nolimits_{{s \in {\mathcal{S}}}} {\sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {n_{sd}^{x} \cdot \varphi_{sd}^{x} \cdot {\text{G}}} } \ge r_{d}^{ *} \quad \forall \,d \in {\mathcal{D}}, $$
(29)
$$ \sum\nolimits_{{d \in {\mathcal{D}}}} {\sum\nolimits_{x = 0}^{{{ \hbox{min} }\left[ {\left( {C_{sd} - B_{sd} } \right) \cdot T,\hbox{min} \left( {\frac{{d_{s}^{ *} }}{\text{G}},\frac{{r_{d}^{ *} }}{\text{G}}} \right)} \right]}} {n_{sd}^{x} \cdot \varphi_{sd}^{x} \cdot {\text{G}}} } \le d_{s}^{ *} \quad \forall \,s \in {\mathcal{S}}, $$
(30)
$$ n_{sd}^{x} \ge 0\,\& \,integer\quad \forall \,s \in {\mathcal{S}},d \in {\mathcal{D}}. $$
(31)

where objective function (25) represents the total transportation time. Constraints (26) and (27) restrict the total number of vehicles on each route. Constraint (28) restricts that only one solution is selected from the set of potential solutions. Constraint (29) restricts that the pre-determined demand should be met. Constraint (30) restricts the outgoing commodity cannot exceed the pre-determined supply. Constraint (31) defines the decision variable.

4 Numerical Analysis

To illustrate the validity of the proposed model and solution approach, a numerical analysis with a randomly generated instance is carried out and the related results are reported. In this numerical instance, 12 relief centers and the commodity of food are considered. In BRP function, α = 0.15 and β = 4.0 are used to estimate the travel time under traffic congestion. The planning period \( T \) equals to 1. Relief-center weight values are integers generated randomly in the interval [10, 30]. The minimum and maximum quantities of demand and supply are integer numbers and drawn randomly from the intervals [5, 15] and [20, 30], respectively. Moreover, the scenarios in each of supply and demand relief centers are consecutive integer numbers from \( S_{cs}^{\Delta } \) to \( S_{cs}^{\nabla } \) with probability \( 1/\left( {S_{cs}^{\nabla } - S_{cs}^{\Delta } + 1} \right) \), and from \( R_{cd}^{\Delta } \) to \( R_{cd}^{\nabla } \) with probability \( 1/\left( {R_{cd}^{\nabla } - R_{cd}^{\Delta } + 1} \right) \) respectively. The commodity has a weight of 2.0 and a volume of 1.0. The vehicle has weight and volume capacities (10, 10). Besides, the vehicle has loading/unloading time 2 and speed 1. The distance between relief centers comes from the interval [20, 60]. The background traffic-flow rates are randomly generated on the interval \( \left[ {0.4,0.8} \right] \). The practical capacity of each route is randomly generated in the interval [60, 100]. All the models are implemented in IBM ILOG CPLEX Optimization Studio (Version: 12.6).

Table 1 shows that 6 relief centers are considered as supply relief centers. The parameters and decision variables at relief centers are also given in Table 1. It is obvious that the incoming and outgoing quantities of commodities are closely related to the weighted values, demand, and supply at relief centers. Generally, a demand relief center with a large weighted value and great demand receives more to meet its high-pressure need. A supply relief center with a small weighted value and great supply shares more with other relief centers. For instance, the fifth demand relief center with weighted value 30 receives more food than the first demand relief center with weighted value 30. The second supply relief center with a weighted value of 28 shares less and maintains a higher food inventory level. To obtain a better insight into the behavior in the transportation process with traffic congestion, the obtained first-stage decision variables are expanded ten times. After that, the vehicle assignment between relief centers is obtained and shown in Table 2.

Table 1. Results of incoming and outgoing food at relief centers in the first stage
Full size table
Table 2. Results of vehicle assignment between relief centers in the second stage
Full size table

5 Conclusion and Future Research

This paper presents a two-stage stochastic mixed-integer nonlinear programming model for the commodity rebalancing considering traffic congestion under uncertainties of demand and supply. A method to linearize the model is developed so that it can be solved in the CPLEX solver. A numerical analysis is applied to demonstrate the applicability of the solution method for the proposed model. In the end, the problem of interests from the following aspects can be explored in future studies. It is interesting to consider the multi-commodity rebalancing cases. It is a significant topic to extend the model to the multi-period rebalancing process. Another future consideration is to extend this work to the budget-based uncertain cases. These questions will be considered in further research.