Abstract
We review various mathematical constructions relevant to the kinematical model of defective crystals that Davini proposed in 1986. Partly, the motivation for this is the need to place quantities that are useful in phenomenological theories of inelastic behaviour (which are many and rather varied) in a general mathematical framework. Partly, too, simple assumptions regarding defective crystal symmetries are inadequate, so a re-evaluation of those assumptions is necessary. Also, as motivation, we take the current effort in continuum mechanics to rationalize the connection between continuum and discrete models of materials, and so review results which elucidate the rigorous connection between continuous and discrete structures in the context of Davini’s model.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Let G be a three dimensional Lie group, with commutator (x, y) ≡x −1 y −1 xy. Let G ≡ G 0 and define G 1 ≡ (G, G 0), the group generated by elements of the form (x, y), x ∈ G, y ∈ G 0. Define G k ≡ (G, G k−1) inductively, k ≥ 1. G is called nilpotent if and only if G k is the trivial group {0} for sufficiently large k. For three dimensional nilpotent groups,
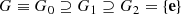 , where e is a temporary notation for the group identity 0.
, where e is a temporary notation for the group identity 0.Let \(\mathbf {\mathfrak {g}}\) be the Lie algebra corresponding to a Lie group G, with Lie bracket \([{\mathbf {{x}}},{\mathbf {{y}}}], {\mathbf {{x}}}, {\mathbf {{y}}}\in \mathbf {\mathfrak {g}}\). Let \(\mathbf {\mathfrak {g}}\equiv \mathbf {\mathfrak {g}}_0\) and define \(\mathbf {\mathfrak {g}}_1 \equiv \left [\mathbf {\mathfrak {g}},\mathbf {\mathfrak {g}}_0\right ]\), the subspace generated by elements of the form \([{\mathbf {{x}}}, {\mathbf {{y}}}],{\mathbf {{x}}}\in \mathbf {\mathfrak {g}}, {\mathbf {{y}}} \in \mathbf {\mathfrak {g}}_0\). Define \(\mathbf {\mathfrak {g}}_k\equiv \left [\mathbf {\mathfrak {g}}, \mathbf {\mathfrak {g}}_{k-1}\right ]\) inductively, k ≥ 1. \(\mathbf {\mathfrak {g}}\) is called nilpotent if and only if \(\mathbf {\mathfrak {g}}_k\) is the trivial subspace {0} for sufficiently large k. For three dimensional nilpotent algebras,
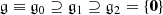 .
.A Lie group is nilpotent if and only if the corresponding Lie algebra is nilpotent (Gorbatsevich, Onishchik, Vinberg [19]).
- 2.
For the motivation of this assumption see [13].
- 3.
A vector field on a manifold M is considered complete if the corresponding flow is globally defined.
- 4.
Given a Lie group G and its closed subgroup G x, the quotient space G∕G x is called a homogeneous manifold if it admits a structure of smooth manifold.
- 5.
The process of composing the actions of one-parameter subgroups to obtain the whole group G acting on the corresponding base space is only valid if the group G is connected [35].
- 6.
The reductivity of a homogeneous space G∕G 0 is usually defined by requiring that there exists a vector space \(\frak {D}\subset \frak {g}\) such that the algebra \(\frak {g}=\frak {g}_0\oplus \frak {D}\) and such that it is invariant under the adjoint action of the subgroup G 0. The condition \([\frak {g}_0,\frak {D}]\subset \frak {D}\) implies the invariance of the distribution \(\frak {D}\) under the adjoint action of the group G 0, but not vice versa. However, when the group G is a connected Lie group, both conditions are equivalent.
Note that not all homogeneous spaces are reductive [44]. Note also that it is not necessarily easy to determine if a given homogeneous space is indeed reductive as it requires finding a vector space complement to \(\frak {g}_0\) in \(\frak {g}\) (among all possible complements) which satisfies the said condition of invariance.
- 7.
See for example [24].
- 8.
The equivariance of the one-form Π is the direct consequence of the assumption that the homogeneous manifold G∕G 0 is reductive as shown in [13].
- 9.
More detailed presentation can be found in [13].
- 10.
To confirm this isomorphism select
$$\displaystyle \begin{aligned}\begin{pmatrix}0&0&0\\ 0&0&-1\\ 0&1&0\end{pmatrix},\: \begin{pmatrix}0&-1&0\\ 1&0&0\\ 0&0&0\end{pmatrix},\: \begin{pmatrix}0&0&-1\\ 0&0&0\\ 1&0&0\end{pmatrix}\end{aligned}$$as a basis of \(\frak {so}(3)\) [2].
References
Auslander, L., Green, L., Hahn, F.: Flows on homogeneous spaces, Annals of Mathematics Studies 53, Princeton University Press, Princeton NJ (1963)
Baker A.: Matrix groups, Springer-Verlag, London (2003)
Bianchi,L.: Lezioni sulla teoria dei gruppi continui finiti di trasformazioni. Enrico Spoerri, Editore, Pisa (1918)
Bilby, B.A.: Continuous distributions of dislocations, in Progress in Solid Mechanics, vol. 1, ed. I. Sneddon, North-Holland, Amsterdam (1960).
Cauchy, A.L.: Sur l’equilibre et le mouvement d’un systeme de points materials sollecites par d’attraction ou de repulsion mutuelle, Ex. de Math., 3, 227–287, (1828)
Cermelli, P., Parry, G.P.: The structure of uniform discrete defective crystals, Continuum Mechanics and Thermodynamics, 18, 47–61 (2006)
Chipot, M., Kinderlehrer, D.: Equilibrium configurations of crystals, Arch. Rat. Mech. Anal., 103, 237–277, (1988)
Crainic, M., Fernandes, R.L.: Integrability of Lie brackets, Annals of Mathematics, 157, 575–620, (2003), https://doi.org/10.4007/annals.2003.157.575
Davini, C.: A proposal for a continuum theory of defective crystals, Arch. Ration. Mech. Anal., 96, 295–317 (1986), https://doi.org/10.1007/BF00251800
Davini, C., Parry, G.P.: On defect-preserving deformations in crystals, Int. J.Plasticity 5, 337–369 (1989), https://doi.org/10.1016/0749-6419(89)90022-3
Davini, C. and Parry, G.P.: A complete list of invariants for defective crystals, Proc. R. Soc. Lond. A 432, 341–365 (1991), Erratum: Proc. R. Soc. Lond. A 434, 735 (1991), https://doi.org/10.1098/rspa1991.0125
Elżanowski, M., Parry G.P.: Material symmetry in a theory of continuously defective crystals, J. Elasticity, 74, 215–237, (2004)
Elżanowski, M., Parry, G.P.: Connection and curvature in crystals with nonconstant dislocation density, Math. Mech. Solids, 1–12 (2018), https://doi.org/10.1177/1081286518791008
Elżanowski, M., Preston, S.: On continuously defective elastic crystals, Miskolc Mathematical Notes, 14(2), 659–670 (2013)
Epstein, M.: The Geometrical Language of Continuum Mechanics, Cambridge University Press, Cambridge (2010)
Fernandes, R.L., Struchiner, I.: The classifying Lie algebroid of a geometric structure I: Classes of coframes. Trans. Ams. Math. Soc., 366, 2419–2462 (2014), https://doi.org/10.1090/S0002-9947-2014-05973-4
Fonseca, I., Parry, G.P.: Equilibrium configurations of defective crystals. Arch. Ration. Mech. Anal., 120, 245–283 (1992), https://doi.org/10.1007/BF00375027
Gorbatsevich, V.V., Onishchik, A.L., Vinberg, E.B.: Lie Groups and Lie Algebras I, Encyclopedia of Mathematical Sciences, Vol. 20, Onishchik, A.L. (ed.), Springer-Verlag, Berlin Heiderberg (1993)
Gorbatsevich, V.V., Onishchik, A.L., Vinberg, E.B.: Foundations of Lie theory and Lie transformation groups, Springer-Verlag, Berlin, Heidelberg (1997)
Green, A.E., Adkins,J.E.: Large Elastic Deformations, (2nd ed.), Oxford University Press, London, Oxford (1970)
Jacobsen, N.: Lie algebras, Dover Publications, New York (1979)
Johnson, D.L.: Presentations of groups, London Mathematical Society Student Texts 15, 2nd edn, Cambridge University Press, Cambridge (1997).
Kobayashi, S.: Transformation Groups in Differential Geometry, Springer-Verlag, Berlin Heidelberg (1995)
Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry, Vol. I, II, John Wiley & Sons, Inc., New York (1996)
Kondo, K.: Non-Riemannian geometry of imperfect crystals from a macroscopic viewpoint. RAAG memoirs of the unifying study of basic problems in engineering and physical science by means of geometry, 1, Gakuyusty Bunken Fukin-Day, Tokyo (1955)
Lee, E.H.: Finite-strain elastic-plastic theory with application. J. of Appl.Physics., 38, 19–27, (1967)
Lee, E.H.: Elastic-plastic deformation at finite strains, J. of App. Mechanics, 36, 1–6, (1969)
Love, A.E.H.: A treatise on the mathematical theory of elasticity, Dover Publications, New York (1927)
Komrakov, B., Churyamov, A., Doubrov, B.: Two-dimensional homogeneous spaces, Preprint Series 17-Matematisk institutt, Universitetet i Oslo (1993)
Magnus, W., Karrass, A., Solitar, D.: Combinatorial Group Theory, Dover, New York (1976)
Mal’cev, A.: On a class of homogeneous spaces, Izv. Akad. Nauk SSSR, Ser. Mat., 13, 9–32, (1949), Am. Math. Soc. Translation, 39, (1949)
Nicks, R., Parry, G.P.: On symmetries of crystals with defects related to a class of solvable groups (S 1), Math. Mech. Solids, 17, 631–651 (2011), https://doi.org/10.1177/1081286511427485
Nicks, R., Parry, G.P.: On symmetries of crystals with defects related to a class of solvable groups (S 2), Mathematical Methods in the Applied Sciences, 35, 1741–1755, (2012)
Olver, P.J.: Applications of Lie Groups to Differential Equations, 2nd edn. Graduate Texts in Mathematics, Vol. 107, Springer-Verlag, Berlin (1993)
Olver, P.J.: Equivalence, Invariants, and Symmetry, Cambridge University Press, Cambridge (1995)
Palais, R.S.: A global formulation of the Lie theory of transformation groups, Mem. Amer. Math. Soc. 22 (1957)
Parry, G.P.: Group properties of defective crystal structures, Math. Mech. Solids, 8, 515–537, (2003)
Parry, G.P.: Rotational Symmetries of Crystals with Defects, J. Elasticity, 94, 147–166, (2009)
Parry, G.P.: Elastic Symmetries of Defective Crystals, J. Elasticity, 101, 101–120, (2010)
Parry, G.P.: Discrete structures in continuum descriptions of defective crystals, Phil.Trans.R.Soc. A, 374, (2015), https://doi.org/10.1098/rsta.2015.0172
Parry, G.P., S̆ilhavý, M.: Elastic invariants in the theory of defective crystals, Proc. R. Soc. Lond. A 455, 4333–4346 (1999), https://doi.org/10.1098/rspa.1999.0503
Parry, G.P., Zyskin, M.: Geometrical structure of two-dimensional crystals with non-constant dislocation density, J.Elast 127, 249–268 (2017), https://doi.org/10.1007/s10659-016-9612-3
Pitteri, M., Zanzotto, G.: Continuum Models for Phase Transitions and Twinning in Crystals, Chapman and Hall, Boca Raton, London, New York, Washington DC (2003)
Poor, W.A.: Differential Geometric Structures, McGraw-Hill, New York (1981)
Pontryagin, L.S.: Topological Groups, 2nd edn. Gordon and Breach, New York, London, Paris (1955)
Rossmann, W.: Lie Groups, An Introduction Through Linear groups, Oxford Graduate Texts in Mathematics; 5, Oxford University Press, Oxford (2006)
Senechal, M.: Quasicrystals and geometry, Cambridge University Press, Cambridge (1995)
Thurston, W.:Three Dimensional Geometry and Topology, vol 1, Princeton University Press, Princeton (1997)
Tricerri, F., Vanhecke, L.: Homogeneous Structures on Riemannian Manifolds, Cambridge University Press, Cambridge (1983)
Varadarajan, V.S.: Lie groups, Lie algebras, and their representations, Prentice–Hall, Englewood Cliffs (1974)
Acknowledgements
We are very grateful to the EPSRC for support provided via Research Grant EP/M024202/1.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Elżanowski, M.Z., Parry, G.P. (2020). A Kinematics of Defects in Solid Crystals. In: Segev, R., Epstein, M. (eds) Geometric Continuum Mechanics. Advances in Mechanics and Mathematics(), vol 43. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-42683-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-42683-5_7
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-42682-8
Online ISBN: 978-3-030-42683-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


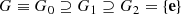 , where e is a temporary notation for the group identity 0.
, where e is a temporary notation for the group identity 0.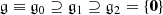 .
.