1 Introduction

A face of a polyhedron is defined as the set of points reaching the maximum (or minimum) of a linear function over the polyhedron. Faces are ubiquitous in the theory of polyhedra, and especially in the complexity analysis of optimization algorithms. As an illustration, the simplex method, one of the most widely used algorithms for solving linear programming, finds an optimal solution by iterating over the graph of the polyhedron, i.e. the adjacency graph of vertices and edges, which respectively constitute the 0- and 1-dimensional faces. The problem of finding a pivoting rule, i.e. a way to iterate over the graph, which ensures to reach an optimal vertex in a polynomial number of steps, is a central problem in computational optimization, related with Smale’s ninth problem for the twenty-first century [25]. Faces of polyhedra are also involved in the worst-case complexity analysis of other optimization methods, such as interior point methods; see [2, 13]. This has motivated several mathematical problems on the combinatorics of faces, which are of independent interest. For example, the question of finding a polynomial bound on the diameter of the graphs of polyhedra (in the dimension and the number of defining inequalities) is still unresolved, despite recent progress [6, 7, 23]. We refer to [12] for a recent account on the subject.

Other applications of polyhedra and their faces arise in formal verification, in which passing from a representation by inequalities to a representation as the convex hull of finitely many points and vice versa, is a critical computational step. The correctness analysis of the algorithms solving this problem, extensively relies on the understanding of the mathematical structure of faces, in particular of vertices, edges and facets (i.e. 1-co-dimensional faces).

In this paper, we formalize a significant part of the properties of faces in the proof assistant Coq. As usually happens in the formalization of mathematics, one of the key difficulties is to find the right representation for objects in the proof assistant. For polyhedra and their faces, the choice of the representation depends on the context. In more detail, every polyhedron admits infinitely many descriptions by linear inequality systems. In mathematics textbooks, proofs are carried out by choosing one (often arbitrary) inequality system for a polyhedron \(\mathcal {P}\), and then manipulating the faces of \(\mathcal {P}\) or other subsequent polyhedra through inequality systems which derive from the one chosen for \(\mathcal {P}\). Proving that these are valid inequality systems is usually trivial for the reader, but not for the proof assistant. We exploit the so-called canonical structures of Coq in order to achieve this step automatically. This allows us to obtain proof scripts which only focus on the relevant mathematical content, and which are closer to what mathematicians write.

Thanks to this approach, we show that the faces of a polyhedron \(\mathcal {P}\) form a finite lattice, in which the order is the set inclusion, the bottom and top elements are respectively the empty set and \(\mathcal {P}\), and the meet operation is the set intersection. We establish that the face lattice is both atomistic and coatomistic, meaning that every element is the join (resp. the meet) of a finite set of atoms (resp. coatoms). Atoms and coatoms respectively correspond to minimal and maximal elements distinct from the top and bottom elements. Moreover, we prove that the face lattice is graded, i.e. every maximal chain has the same length. Finally, we show that the family of face lattices of polytopes (convex hulls of finitely many points) is closed under taking sublattices, i.e. any sublattice of the face lattice of a polytope is isomorphic to the face lattice of another polytope. As a consequence of that, we prove that any sublattice of height two is isomorphic to a diamond.

Formalizing these results requires the introduction of several important and non-trivial notions. First of all, our work relies on the construction of a library manipulating polyhedra, which provides all the basic operations over them, including intersections, projections, convex hulls, as well as special classes of polyhedra such as affine subspaces. Dealing with faces also requires to formalize the dimension of a polyhedron, and its relation with the dimension of its affine hull, i.e. the smallest affine subspace containing it. Some classes of faces also retain a particular attention, such as vertices, edges and facets. For instance, we formalize the vertex figure, which is a geometric construction to manipulate the faces containing a fixed vertex.

Throughout this work, we have drawn much inspiration from the textbooks of Schrijver [24] and Ziegler [28] to guide us in our approach. The source code of our formalization is done within the Coq-Polyhedra project, and is available at https://github.com/Coq-Polyhedra/Coq-Polyhedra/tree/IJCAR-2020, in the directory . We rely on the Mathematical Components library [18] (abridged MathComp thereafter) for basic data structures such as finite sets, ordered fields, and vector spaces.

The paper is organized as follows. In Sect. 2, we present how we define the basic operations and constructions over polyhedra. Section 3 deals with the central problem of finding an appropriate representation of faces, and explains how this leads to a seamless formalization of important properties like the dimension. Section 4 demonstrates the practical usability of our approach, by presenting the formalization of the face lattice and its main characteristics. Finally, we discuss related work in Sect. 5. A link to the relevant source files is given beside section titles in order to help the reader finding the results in the source code of the formalization.

2 Constructing a Library Manipulating Polyhedra

2.1 The Quotient Type of Polyhedra\(^{,}\)

We recall that a (convex) polyhedron of \(\mathbb {R}^n\) is defined as the intersection of finitely many halfspaces \(\{x \in \mathbb {R}^n :\langle \alpha , x \rangle \ge \beta \}\), where \(\alpha \in \mathbb {R}^n\), \(\beta \in \mathbb {R}\), and \(\langle \cdot , \cdot \rangle \) is the Euclidean scalar product, i.e. . Equivalently, a polyhedron can be represented as the solution set of a linear affine system \(A x \ge b\), where \(A \in \mathbb {R}^{m \times n}\) and \(b \in \mathbb {R}^m\), in which case each inequality \(A_i x \ge b_i\) corresponds to a halfspace.

Throughout the paper, we use the variable to represent the dimension of the ambient space. Instead of dealing with polyhedra over the reals, we introduce a variable which represents an abstract ordered field with decidable ordering. In this setting, (or for short) stands for the type of column vectors of size over the field .

As we mentioned earlier, the representation by inequalities (or halfspaces) of a convex polyhedron \(\mathcal {P}\) is not unique. The first step in our work is to introduce a quotient structure, in order to define the basic operations (membership of a point, inclusion, etc.) regardless of the exact representation of the polyhedron. The quotient structure is based on a concrete type denoted by (or simply , when is clear from the context). The prefix letter “h” is taken from the terminology H-polyhedron or H-representation which is used to refer to representations by halfspaces. The elements of are records consisting of a matrix \(A \in \mathbb {R}^{m \times n}\) and a vector \(b \in \mathbb {R}^m\) representing the system \(A x \ge b\):

figure l

We equip with a membership predicate stating that, given and , we have if and only if satisfies the system of inequalities represented by . Two H-polyhedra are equivalent when they correspond to the same solution set, i.e. their membership predicate agree. We prove that this equivalence relation is decidable, by exploiting the implementation of the simplex method of [3]. The latter allows us to check that an inequality \(\langle \alpha , x \rangle \ge \beta \) is valid over an H-polyhedron by minimizing the linear function \(x \mapsto \langle \alpha , x \rangle \) over , and checking that the optimal value is greater than or equal to \(\beta \). Then, deciding whether are equivalent amounts to checking that each inequality in the system defining is valid over , and vice versa.

The quotient structure is built following the approach of [10]. This introduces a quotient type, denoted here by (or simply ). Its elements are referred to as polyhedra and represent equivalence classes of H-polyhedra. In practice, each polyhedron is a record formed by a canonical representative of the class, and the proof that the representative is indeed the canonical one. We point out that the notion of canonical representative has no special mathematical meaning or structure.

We define the membership predicate of each as the membership predicate of its canonical representative. As expected, equality between two polyhedra of and extensional equality (denoted below) of their membership predicates are equivalent properties:

figure ac

2.2 Operations over Polyhedra

We first lift a number of basic primitives from the type to the quotient type , including the subset relation and the intersection operation . The related properties are also lifted by using the fact that the membership predicate of any element of is extentionally equivalent to the membership predicate of its equivalence class in .

Even though we now work on the quotient type, we still need a way to build polyhedra from sets of inequalities. While H-polyhedra rely on inequality constraints under the matrix form, we choose now to be closer to the mathematical definition of polyhedra as the intersection of finitely many halfspaces. To this end, we introduce the type (or simply when is clear from the context), which is isomorphic to the cartesian product of vectors of size and elements of . This type is used to construct linear affine inequalities or equalities. In more detail, if represents the pair \((\alpha , \beta ) \in \mathbb {R}^n \times \mathbb {R}\), then the polyhedron corresponds to the halfspace \(\langle \alpha , x \rangle \ge \beta \):

figure ar

Similarly, the element is used to build a hyperplane denoted :

figure au

(In the last two statements, the terms and respectively stand for the first and second component of the pair formed by , while stands for the scalar product between two vectors.)

We can now construct polyhedra defined by sets of inequalities. To this aim, we use the type of finite sets of elements of type . Then, given , the polyhedron denoted by is defined as the intersection of the halfspaces for . In particular, we introduce the empty polyhedron and the full polyhedron , which are defined by the inequality \(1 \le 0\) and by no inequality respectively. As we shall see in Sect. 3, the formalization of faces requires us to manipulate polyhedra defined by systems mixing inequalities and equalities. We denote such a polyhedron by , where both and are of type . It represents the intersection of the polyhedron with the hyperplanes for .

The cornerstone of more advanced constructions is the primitive , which, given , builds its projection on the last components. This is carried out by implementing Fourier–Motzkin elimination algorithm (see e.g. [24, Chapter 12]). In short, this algorithm starts from a system of linear inequalities, and constructs pairwise combinations of them in order to eliminate the first variable. The result is that the new system is a valid representation of the projected polyhedron. This is written as follows:

figure br

where is the projection of on the last components, and stands for a logical equivalence between the two properties. This projection primitive then allows us to construct many more polyhedra. For example, we can build the image of a polyhedron \(\mathcal {P}\) by the linear map represented by a matrix \(A \in \mathbb {R}^{k \times n}\). The latter is obtained by embedding \(\mathcal {P}\) in a polyhedron over the variables \((x,y) \in \mathbb {R}^{n+k}\), intersecting it with the equality constraints \(y = A x\), and finally projecting it on the last k components. The construction of the convex hull of finitely many points immediately follows. Indeed, the convex hull of a finite set \(V = \{v^1, \dots , v^p\} \subset \mathbb {R}^n\) can be defined as the image of the simplex by the linear map \(\mu \mapsto \sum _{i = 1}^p \mu _i v^i\). We denote the convex hull by where represents a finite set of points, and we obtain (cf.  ) that if and only if is a barycentric combination of the points of . The convex hull constructor yields some other elementary yet very useful constructions, such as polyhedra reduced to a single point (denoted where ) or segments between two points (denoted where ).

Finally, we recover some important results of the theory of polyhedra which were proved in [3]. In more detail, we lift a version of Farkas Lemma expressed on the type , and then obtain the Strong Duality Theorem, the complementary slackness conditions (which are conditions characterizing the optimality of solutions of linear programs), and some separation results. We refer to and for further details on these statements.

3 Representing Faces of Polyhedra

https://github.com/Coq-Polyhedra/Coq-Polyhedra/tree/IJCAR-2020/theories/poly_base.v.

3.1 Equivalent Definitions of Faces

Faces are commonly defined as sets of optimal solutions of linear programs, i.e. problems consisting in minimizing a linear function over a polyhedron.

Definition 1

A set \(\mathcal {F}\) is a face of the polyhedron \(\mathcal {P}\subset \mathbb {R}^n\) if \(\mathcal {F}= \emptyset \) or there exists \(c \in \mathbb {R}^n\) such that \(\mathcal {F}\) is the set of points of \(\mathcal {P}\) minimizing the linear function \(x \mapsto \langle c, x \rangle \) over \(\mathcal {P}\).

We note that \(\mathcal {P}\) is a face of itself (take \(c = 0\)). Figure 1 provides an illustration of this definition.

Fig. 1.
figure 1

A polyhedron, defined by the inequalities on the right, and its faces. The vertices (0-dim. faces) are represented by blue dots, while the edges (1-dim. faces) are depicted in black. Arrows correspond to linear functions associated with some of the faces, in the sense of Definition 1. We also indicate beside them the set I of the defining inequalities turned into equalities, as in Theorem 1. (Color figure online)

Full size image

In formal proving, the choice of the definition plays a major role on the ability to prove complex properties of the considered objects. A drawback of the previous definition is that it does not directly exhibit some of the most basic properties of faces: for instance, the fact that a face is itself a polyhedron, the fact that the intersection of two faces is a face, or the fact that a polyhedron has finitely many faces. In contrast, these properties are straightforward consequences of the following characterization of faces:

Theorem 1

Let \(\mathcal {P}= \{ x \in \mathbb {R}^n :A x \ge b \}\), where \(A \in \mathbb {R}^{m \times n}\) and \(b \in \mathbb {R}^m\). A set \(\mathcal {F}\) is face of \(\mathcal {P}\) if and only if \(\mathcal {F}= \emptyset \) or there exists \(I \subset \{1, \dots , m\}\) such that

$$\begin{aligned} \mathcal {F}= \mathcal {P}\cap \{ x \in \mathbb {R}^n :A_i x = b_i \; \text {for all} \; i \in I \}. \end{aligned}$$
(1)

Nevertheless, Theorem 1 is expressed in terms of a certain H-representation of the polyhedron \(\mathcal {P}\), while the property of being a face is intrinsic to the set \(\mathcal {P}\). This raises the problem of exploiting the most convenient representation of \(\mathcal {P}\) to apply the characterization of Theorem 1. We illustrate this on the proof of the following property, which is used systematically (or even implicitly) in almost every proof of statements on faces:

Proposition 1

If \(\mathcal {F}\) is a face of \(\mathcal {P}\), then any face of \(\mathcal {F}\) is a face of \(\mathcal {P}\).

Assume \(\mathcal {P}\) is represented by the inequality system \(A x \ge b\), and take I as in (1). Let \(\mathcal {F}'\) be a nonempty face of \(\mathcal {F}\). We apply Theorem 1 with \(\mathcal {F}\) as \(\mathcal {P}\), by using the following H-representation of \(\mathcal {F}\) : \(A x \ge b\) and \(-A_i x \ge -b_i\) for \(i \in I\). We get that \(\mathcal {F}' = \mathcal {F}\cap \{ x \in \mathbb {R}^n :A_i x = b_i \; \text {for all} \; i \in I' \}\) for a certain set \(I' \subset \{1, \dots , m\}\). We deduce that \(\mathcal {F}' = \mathcal {P}\cap \{ x \in \mathbb {R}^n :A_i x = b_i \; \text {for all} \; i \in I \cup I' \}\), and conclude that \(\mathcal {F}'\) is a face of \(\mathcal {P}\) by applying Theorem 1. While the choice of the H-representation of \(\mathcal {P}\) is irrelevant, we point out that the proof would not have been so immediate if we had initially chosen an arbitrary H-representation of \(\mathcal {F}\).

3.2 Working Within a Fixed Ambient H-Representation

Theorem 1 leads us to the following strategy: when dealing with the faces of a polyhedron, and possibly with the faces of these faces, etc., we first set an H-representation of the top polyhedron, and then manipulate the subsequent H-representations of faces in which some inequalities are strengthened into equalities, like in (1).

The top H-representation will be referred to as the ambient representation, and is formalized as a term of type representing a finite set of inequalities. Then, we introduce the type , which corresponds to the subtype of whose inhabitants are the polyhedra satisfying the following property:

figure co

where is the type of subsets of . We recall that denotes the polyhedron defined by the inequalities in , with the additional constraint that the inequalities in the subset are satisfied with equality. This means that corresponds to the polyhedra defined by equalities or inequalities in . The choice of the name is reminiscent of the terminology used in fiber bundles. Indeed, as we shall see in the next sections, several proofs will adopt the scheme of fixing a base locally, and then working on polyhedra of type . Following this analogy, the latter may be thought of as a fiber.

We now present a first formalization of the set of faces relying on the subtype :

figure cz

It defines the set of faces of as the set of elements of contained in . With this definition, some properties of faces come for free. For instance, the finiteness of the set of faces follows from the fact that there are only finitely many inhabitants of the type , and subsequently of . Another example is that Proposition 1 straightforwardly derives from the transitivity of the inclusion relation .

Some other properties come at the price of proving that a polyhedron inhabits the type . As an example, if and , the polyhedron is defined as the set of points of minimizing the function . Showing that is a face of essentially amounts to proving the following property:

figure do

Indeed, the inclusion is immediate from the definition of the polyhedron . However, even once is proved, we cannot yet write a statement of the form due to the fact that has type . In order to turn it into an element of the subtype , we need to explain in more detail how this type is defined. The type is a short-hand notation for the following inductive type:

figure dx

In other words, an element of type is a record formed by an element and a proof that the property holds. While we could construct the element , we introduce a more general scheme to cast elements of type to whenever possible. This scheme relies on Coq canonical structures, which provide an automatic way to recover a term of record type from the head symbol. The association is declared as follows:

figure ee

One restriction of Coq is that canonical structures are resolved only when unifying types, and not arbitrary terms. This is why our primitive , which casts a to a , encapsulates the value in a phantom type, i.e. a type isomorphic to the unit type, but with a dependency to  .

figure ek

In consequence, writing triggers the unification algorithm between the term and a value of type , which is resolved using the declared above. We finally end up with the following statement

figure ep

whose proof is trivial: it just amounts to proving the inclusion .

We declare other canonical structures over elementary constructions for which the property can be shown to be satisfied. This includes the intersection of two elements , the empty set , or polyhedra of the form or . This allows us to cast complex terms to the type , or, said differently, to prove automatically that they satisfy the property . As an example, the term

figure ez

typechecks thanks to multiple resolutions of canonical structures on the aforementioned declarations, without requiring extra proof from the user. We refer to [21] for the use of canonical structures in formal mathematics.

We point out that is a proof of one side of the equivalence between the definition of faces brought by and Definition 1 (i.e. the equivalence in Theorem 1). The other side can be written as follows:

figure fc

When is nonempty, we use a set such that , and we build as the sum of the vectors for . The equality follows from a routine verification of the complementary slackness conditions.

3.3 Getting Free from Ambient Representations

So far, we have worked with a fixed ambient representation , and restricted the formalization of faces to polyhedra that can be expressed as terms of type . We now describe how to formalize the set of faces of any polyhedron of type as a finite set of polyhedra of the same type, without sacrificing the benefits brought by .

First, we exploit the observation that for each polyhedron , there exists and such that (recall that also stands for the coercion from the type to ). This can be proved by exploiting the definition of the quotient type . Indeed, admits a representative corresponding to a certain H-representation, from which we can build a term such that

Second, we introduce another quotient structure over the type , in order to deal with the fact that a polyhedron may correspond to several elements of type for different values of . Our construction amounts to showing that is isomorphic to the quotient of the dependent sum type by the equivalence relation in which and are equivalent if . Given a polyhedron of type , this construction provides us a canonical ambient representation denoted , and an associated canonical representative of type satisfying .

We are now ready to define the set of faces of in full generality:

figure gq

which corresponds to the image by the coercion of the face set of (here, has type ). Of course, we need to check that this definition is independent of the choice of the representative of in this new quotient structure. This is written as follows:

figure gw

The proof relies on the geometric properties of the elements of established in Sect. 3.2. Indeed, they imply that, regardless of the choice of the ambient representation, the set always consists of the empty set and the polyhedra of the form .

Now that this architecture is settled, we can prove some of the basic properties of faces. Most of the proof make use of the following elimination principle:

figure hb

which means that, given a property to be proved on any polyhedron , it is sufficient to prove it over the type for any choice of . In practice, is used to introduce an ambient representation. Let us illustrate it on the proof that the intersection of two faces of is a face of :

figure hi

The first line destructs , and introduces the ambient representation and an element still named , now of type . The second and third lines successively consume the assumptions that and are faces, then introduce two elements of type having the same name and respectively satisfying and . Finally, the tactics replaces the goal by the following two subgoals: and . Since and , the former is proved by transitivity of the subset relation. The latter is automatically provided by the canonical structure mechanism described in Sect. 3.2, triggered by the generic statement

figure hy

3.4 From Faces to the Affine Hull and Dimension

We argue that the approach that we have introduced to represent faces of polyhedra also perfectly fits the formalization of the affine hull and dimension of polyhedra. Recall that the affine hull of a polyhedron refers to the smallest (inclusionwise) affine subspace of \(\mathbb {R}^n\) containing it, and the dimension of the polyhedron is defined as the dimension of this subspace (i.e., the dimension of the underlying vector subspace).

To this end, given an ambient representation and a polyhedron of type , we introduce the set of active inequalities of , i.e. the set of such that the corresponding inequality is satisfied as equality over . This is written as the inclusion (recall that is the hyperplane ). The active inequalities form a subset of denoted . Equivalently, when is non-empty, corresponds to the largest (inclusionwise) subset such that .

It is a classic property of polyhedra that the affine hull of a non-empty polyhedron is the affine subspace defined by the equalities in . We take this property as a definition:

figure ip

The second definition lifts the affine hull from to . Of course, we show that the resulting affine subspace is independent of the choice of (cf.  ). We establish that this definition is correct w.r.t. the usual mathematical definition discussed above, i.e.:

figure iv

Here, corresponds to a vector subspace of , and the term stands for the affine subspace given by the intersection of the affine equalities represented by the elements of . (The term above corresponds to the vector subspace spanned by the elements of .)

We follow the same scheme to formalize the dimension of a polyhedron , which we define as one plus the co-dimension of the vector span of . The shift by one originates from the fact that ranges over the type of natural numbers. Therefore, we have to set the dimension of the empty set to 0, while it is common to set it to \(-1\) in the literature. As expected, we obtain the following statement:

figure ji

Like in mathematics textbooks, is the natural way to establish the basic statements concerning the dimension, i.e. by reducing to elementary proofs over vector spaces. For instance, we establish that the dimension is monotone ( ), and compute the dimension for important classes of polyhedra. This includes the fact that segments of two distinct points have dimension (remember the shift by one of our formalization):

figure jm

and that, conversely, any compact polyhedron of dimension 2 is a segment of two points:

figure jn

(We point out that is simply defined as the fact that is a bounded set, as polyhedra are topologically closed.) Similarly, we prove that polyhedra reduced to a single point are precisely the ones having dimension 1, that proper hyperplanes have codimension 1, etc. We refer to for a detailed account of our results.

4 The Face Lattice

https://github.com/Coq-Polyhedra/Coq-Polyhedra/tree/IJCAR-2020/theories/poly_base.v.

In this section, we illustrate how the framework that we have introduced in Sect. 3 serves as a foundation for formalizing the structural properties of faces. We refer to Fig. 2 for an example of the properties presented below.

At the core of the formalization lies the theory of ordered structures such as partial orders, semilattices and lattices. Some of these structures have been very recently introduced in the MathComp library – for instance, the non-distributive lattice structure has been introduced in early 2020. However, as we shall see in this section, the formalization of the face lattice requires to implement additional objects, such as graded lattices, sublattices, and lattice homomorphisms. This development is gathered in the module of the Coq-Polyhedra project.

The first property that we can immediately formalize following the results of Sect. 3 is the finite lattice structure over the set for . The partial order is given by the polyhedron inclusion , the meet operator is the intersection (as a consequence of ), while the bottom and top elements are respectively and . As a finite lattice, the join operator can be built as the meet of all the faces of containing both and .

Fig. 2.
figure 2

A three-dimensional polytope (left) and the Hasse diagram of its face lattice (right). A interval of height 2 is depicted in blue. (Color figure online)

Full size image

4.1 Facets and Gradedness

Recall that a lattice \((L, \prec )\) is said to be graded if there exists a rank function \(\Phi :L \rightarrow \mathbb {N}\) such that: (i) \(\Phi (u) < \Phi (v)\) whenever \(u \prec v\), (ii) \(u \preceq v\) and \(\Phi (u)+1 < \Phi (v)\) implies that there exists \(w \in L\) satisfying \(u \prec w \prec v\). Equivalently, this is a lattice in which all maximal chains have the same length.

In the case of the face lattice, the rank function can be defined as the dimension of the face. Property (i) is proved as follows. If and are both faces of and , then , as the dimension is monotone. Moreover, . If we assume , then we can prove that is equal to (as affine subspaces of the same dimension). We conclude that by the fact that for any face of  .

The proof of Property (ii) (see ) relies on the formalization of facets of polyhedra, and their combinatorial characterization in terms of active inequalities. We recall that a facet of a non-empty polyhedron \(\mathcal {P}\) is a face of \(\mathcal {P}\) of dimension \(\dim \mathcal {P}- 1\). A classical result states that when \(\mathcal {P}\) is given by a non-redundant system of inequalities \(A x \ge b\) (i.e. the H-representation is minimal inclusionwise), the facets are precisely the polyhedra of the form \(\mathcal {P}\cap \{ x \in \mathbb {R}^n :A_i x = b_i\}\) for any i such that \(\mathcal {P}\not \subset \{ x \in \mathbb {R}^n :A_i x = b_i\}\). The formalization of this statement first goes through the construction of non-redundant bases for any polyhedron, and the proof of the following elimination principle:

figure kr

This allows to specialize to a polyhedron of the form where is a minimal set of inequalities defining . Using the techniques of Sect. 3, we switch to a proof environment dealing with polyhedra in , and establish that the facets of are precisely the polyhedra of the form for (where is the singleton consisting of ). We refer to the statements and for the exact description.

Going back to the description of the proof of Property (ii), we assume that and are two faces of satisfying and . We first consider the case where . Since , we can pick an element in but not in , and verify that the facet satisfies . The general case where is a proper face of is handled by using the fact that and ensures that is a face of (see ).

4.2 Vertices, Atomicity and Coatomicity

The atoms of a lattice L are the elements \(u \in L \setminus \{\bot \}\) such that there is no \(v \in L\) satisfying \(\bot \prec v \prec u\), where \(\bot \) denotes the bottom element of L. In the face lattice of a polyhedron , they correspond to the faces of such that , i.e. to the vertices of (remember the shift by one of our formalization). This motivates the introduction of the vertex set of , which satisfies the following two characteristic properties:

figure md

A central property is that if is compact, then it coincides with the convex hull of its vertices:

figure mf

Remark that this shows that any compact polyhedron is a polytope. Together with the converse statement ( in ), this brings a proof of Minkowski Theorem.

The latter result allows us to prove that, when is compact, its face lattice is atomistic, meaning that any face of is the join of a finite set of atoms:

figure mk

To prove this statement for , we set to the set of vertices of . The latter are vertices of as well, and thus correspond to atoms of the face lattice of . The inclusion is established by substituting by thanks to , which makes the statement obvious by construction of the convex hull and the join operator. The opposite inclusion is trivial by property of the join operator, and this concludes the proof.

The coatoms of L are defined dually: these are the elements \(u \in L \setminus \{\top \}\) such that there is no \(v \in L\) satisfying \(u \prec v \prec \top \), where \(\top \) denotes the top element of L. The coatomicity of means that any face of is the intersection of facets of . Our proof exploits the characterization of facets presented in Sect. 4.1. We refer to for more details.

4.3 Closedness Under Taking Sublattices

The closedness under sublattices of the face lattices of polytopes states that if and are two faces of a polytope such that , then the interval , i.e. the sublattice formed by the faces satisfying , is isomorphic to the face lattice of a polytope of dimension .

The interest of this property is that it allows involved induction schemes on the height of the face lattice. As an example, we can establish the so-called diamond property, namely that every sublattice of height 2 of the face lattice consists of precisely four faces ordered as . Equivalently, this means that for any two faces \(\mathcal {F}\) and \(\mathcal {F}'\) of a polytope \(\mathcal {P}\) such that \(\dim \mathcal {F}' = \dim \mathcal {F}+ 2\) and \(\mathcal {F}\subset \mathcal {F}'\), there are precisely two faces between them (see  for the statement, and Fig. 2 for an illustration). The proof exploits the closedness by sublattices, and the subsequent isomorphism of any interval of height 2 with the face lattice of a polytope verifying . reduces it to the face lattice of a segment , which is given by the following characterization:

figure nn

The proof of the closedness by sublattices is done as follows. First, we reduce to the case where , since the face lattice of is isomorphic to the sublattice of the faces of contained in . We are left with the following statement:

figure ns
Fig. 3.
figure 3

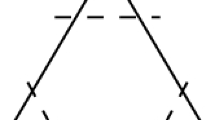
The vertex figure construction, illustrated on the vertex x of the polytope \(\mathcal {P}\). The hyperplane \(\mathcal {H}\) (light blue) separates x from the other vertices of the polytope. In the sliced polytope \(\mathcal {P}'\), the vertices (green) and edges (blue) are respectively in one-to-one correspondence with the edges and facets of \(\mathcal {P}\) containing x. (Color figure online)

Full size image

The proof is done by induction on the dimension of . We restrict the exposition to the base case , i.e. when corresponds to a vertex of , since the general case is just handled by iterating the process. When , the construction of the polyhedron is achieved by the vertex figure method. It consists in slicing the polytope with a hyperplane separating the vertex from the other vertices (see Fig. 3 for an illustration). We define as the sliced polytope. It has dimension , and its face lattice can be shown to be isomorphic to the sublattice . Once again, the isomorphism is proved by exposing the polyhedron to the subtype for some ambient representation , and reducing to basic manipulations of sets of active inequalities of faces. Interestingly, two distinct ambient representations are used in the proof: for the original polytope , and its union with the singleton for the sliced polytope . Our use of canonical structures still applies to this setting, and provides the proof that any face of sliced with the hyperplane writes down over the base of the sliced polytope .

5 Related Work

Many software developments related with convex polyhedra have been motivated by applications to formal verification. Several libraries have been developed for this purpose, e.g. [4, 20], and, despite being informal, it is worth noting that they are also used by mathematicians to perform computation over polyhedra and polytopes, for instance in [16, 27]. Initiatives on the development of formally verified polyhedral algorithms are more recent. The works of [26] and [8] in Isabelle/HOL aim at providing a formally proven yet practical and efficient algorithm to decide linear rational arithmetic for SMT-solving. The Micromega tactics [5] relies on polyhedra to prove automatically arithmetic goals over ordered rings in Coq. The Verified Polyhedral Library [9, 15] targets abstract interpretation, and brings the ability to verify polyhedral computations a posteriori in Coq.

There are far fewer developments focusing on formal mathematics. Euler formula, which relates the number of vertices, edges and facets of three-dimensional polytopes, has been proved in [14] in Coq and in [1] in Mizar. The generalization to polytopes in arbitrary dimension, namely Euler–Poincaré formula, has been formally proved in HOL-Light [19], together with several intermediate properties of polyhedra and faces. In the intuitionistic setting, we are not aware of any work concerning faces and their properties. We point out that Fourier–Motzkin elimination has been formalized in Coq by [22].

6 Conclusion and Future Work

In this work, we have formalized a substantial part of the theory of polyhedra and their faces, which has allowed us to obtain some of the essential properties of face lattices. Beyond the mathematical results formally proven, a special attention has been paid to the usability of the library. This goes through a mechanism to bring the right representation of faces according to the context, and the automatic proof that these representations are valid thanks to the use of canonical structures.

This foundational work opens several perspectives. First, it has raised that an important development over ordered structures is still needed, in particular for the manipulation of ordered substructures such as sublattices, and the interplay between them through morphisms. The formalization of finite groups and subgroups in [17] may provide a possible source of inspiration to solve this problem. Second, there are many other interesting properties in relation with polyhedra and their faces to be formalized, such as getting upper bounds on the diameter of polytopes, or more generally, on the number of faces (the so-called f-vector theory). However, beyond the interest of formalizing already known mathematical results, we are even more interested in using proof assistants to help getting new ones. We think of mathematical results relying on computations that are not accessible by hand. To this extent, we aim at providing a way to compute with the objects introduced in this work, directly within the proof assistant, and to introduce all the needed mechanisms for the design and development of large scale reflection tactics. A basic goal is to compute the face lattice (or part of it) of a polyhedron defined by a set of inequalities. This requires us to formalize some algorithms based on faces, and to find a way to execute them on efficient data structures, in the spirit of the approach of [11].