Abstract
Tensor algebra deals with lifeless vectors and tensors—objects that do not move, do not change, possess no dynamics. Whenever there is a need for tensors in physics, there is also a need to know the way these tensors change with position and time. Tensors that depend on position and time are called tensor fields and are the subject of this chapter.
In studying the algebra of tensors, we learned that they are generalizations of vectors. Once we have a vector space  and its dual space
and its dual space  , we can take the tensor products of factors of
, we can take the tensor products of factors of  and
and  and create tensors of various kinds. Thus, once we know what a vector is, we can make up tensors from it.
and create tensors of various kinds. Thus, once we know what a vector is, we can make up tensors from it.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Recall that an open subset U is one each of whose points is the center of an open ball lying entirely in U.
- 2.
The domain of μ∘f∘φ −1 is not all of \(\mathbb{R}^{m}\), but only its open subset φ(U). However, we shall continue to abuse the notation and write \(\mathbb{R}^{m}\) instead of φ(U). This way, we do not have to constantly change the domain as U changes. The domain is always clear from the context.
- 3.
Although Proposition 17.4.6 was shown for normed linear spaces, it really holds for all “spaces” for which the concept of open set is defined.
- 4.
We usually use u or t to denote the (real) argument of the map γ:[a,b]→M.
- 5.
See the last statement of Definition 28.2.5.
- 6.
Recall that a typical element of
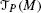 is a map \(\textbf{t}:F^{\infty}(P)\to\mathbb{R}\) for which composition is meaningless.
is a map \(\textbf{t}:F^{\infty}(P)\to\mathbb{R}\) for which composition is meaningless. - 7.
In mathematical jargon,
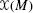 and
and 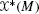 are called modules over the (ring of) real-valued functions on M. Rings are a generalization of the real numbers (field of real numbers) whose elements have all the properties of a field except that they may have no inverse. A module over a field is a vector space.
are called modules over the (ring of) real-valued functions on M. Rings are a generalization of the real numbers (field of real numbers) whose elements have all the properties of a field except that they may have no inverse. A module over a field is a vector space. - 8.
Note how in the wedge product, the first factor has a lower index (is an “earlier” coordinate) than the second factor. If this restriction is to be removed, we need to introduce a factor of \({{\frac{1}{2}}}\) for each component (see Example 28.5.12).
- 9.
The factor \({{\frac{1}{2}}}\) is introduced here to avoid restricting the sum over α and β.
- 10.
Gauge invariance and gauge theories are discussed in detail in Chap. 35.
- 11.
Recall from Chap. 17 that a subset of \(\mathbb{R}^{n}\) is compact iff it is closed and bounded. It is a good idea to keep this in mind as a paradigm of compact spaces.
- 12.
Reader, see where this fact is used!
- 13.
Here, we are assuming that the mechanical system in question is nonsingular, by which is meant that there are precisely n independent p i ’s. There are systems of considerable importance that happen to be singular. Such systems, among which are included all gauge theories such as the general theory of relativity, are called constrained systems and are characterized by the fact that \(\pmb{\omega}\) is degenerate. Although of great interest and currently under intense study, we shall not discuss constrained systems in this book.
References
Abraham, R., Marsden, J.: Foundations of Mechanics, 2nd edn. Addison-Wesley, Reading (1985)
Abraham, R., Marsden, J., Ratiu, T.: Manifolds, Tensor Analysis, and Applications, 2nd edn. Springer, Berlin (1988)
Bishop, R., Goldberg, S.: Tensor Analysis on Manifolds. Dover, New York (1980)
Warner, F.: Foundations of Differentiable Manifolds and Lie Groups. Springer, Berlin (1983)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Analysis of Tensors. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_28
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_28
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


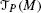 is a map
is a map 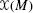 and
and 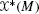 are called modules over the (ring of) real-valued functions on M. Rings are a generalization of the real numbers (field of real numbers) whose elements have all the properties of a field except that they may have no inverse. A module over a field is a vector space.
are called modules over the (ring of) real-valued functions on M. Rings are a generalization of the real numbers (field of real numbers) whose elements have all the properties of a field except that they may have no inverse. A module over a field is a vector space.