Keywords

1 Introduction

Visual tracking is an important task in computer vision [1–3]. Many scholars pay close attention to this research area, because it is widely applied in civil and military fields, such as visual surveillance, intelligent transportation, medial diagnose, military guidance, et al. However, object’s scale changing and background’s interference are the major reasons leading to tracking failure.

In the past decade, many methods are proposed in visual tracking. The mean shift tracking algorithm [4, 5] is a classical kernel tracking methods, which accomplish the tracking task using object’s color histogram. However, for the lack of space information of object and the influence of background feature, the optimal location of object obtained by Bhattacharyya coefficient may not be the exact target location. Zhuang [6] proposes an algorithm which build discriminative sparse similarity map using multiple positive target templates and hundreds of negative templates, and then find the candidate that scores highest in the evaluation model based on discriminative sparse [7] similarity map. However, the algorithm can’t get optimal candidate when the tracking environment is complicated. In [8], the author describes target using distribution fields which can alleviate the influence of space information. But there will be drifted or even wrong location when the object’s scale and pose change obviously. Ning proposes a corrected background-weighted histogram algorithm (CBWH) [9] which can reduce background’s interference by transforming only the target model but not the target candidate model.

Henriques proposed a Tracking-by-detection algorithm [10] based on circular structure, which establish target model by constructing circular structure matrix. The algorithm not only can effectively alleviate the interference of background, but also can improve tracking efficiency. However, the algorithm has one critical drawback: it is likely to lose the object when the object’s scale changes obviously. Considering the advantages and disadvantages of the algorithm, we propose a scale adaptive tracking algorithm based on kernel ridge regression and Fast Fourier Transform. Firstly, the algorithm establish regression model and get object’s location in the search region using regression model. Secondly, it presents a method that estimates the best scale by considering the weight image [11] of all pixels in the candidate region.

2 Regression Model

Kernel ridge regression (KRR) [12] is an important algorithm which can solve non-linear problem that can’t deal with using linear algorithms in original space. In this part, we will introduce the algorithm theory of KRR and method that improves the solving efficiency based on Fast Fourier Transform.

2.1 Algorithm Theory of KRR

Linear regression is a statistic method that is used to establish relation between two or more variables. A linear regression has the form

$$ \varvec{y} = \varvec{w}^{\text{T}} \varvec{x} + \zeta $$
(1)

Where, \( \varvec{w}^{\text{T}} \varvec{x} \) is the dot product of vectors, \( \zeta \) is the deviation between true and evaluation.

The loss function is defined as

$$ {\text{J(}}\varvec{w} ) { = }\sum\limits_{i = 1}^{N} {(y_{i} - \varvec{w}^{\text{T}} \varvec{x}_{i} - \zeta )^{2} } + \lambda ||\varvec{w}||_{2}^{2} $$
(2)

Where, \( \lambda \) controls the amount of regularization.

Trick regression is given by

$$ \hat{\varvec{w}}_{ridge} = \varvec{x}^{\text{T}} (\lambda {\text{I}}_{\text{N}} + \varvec{x}^{\text{T}} \varvec{x})^{ - 1} \varvec{y} $$
(3)

However, trick regression is limited by non-linear problem. It is well known that the kernel trick can improve performance further by allowing a rich high-dimensional feature space. The kernel trick regression is computed as

$$ \hat{\varvec{w}}_{kernel} = \varvec{x}^{\text{T}} (\lambda {\text{I}}_{\text{N}} + K)^{ - 1} \varvec{y} $$
(4)

Note that the input \( \varvec{x} \) is mapped to the feature space and \( K \) is defined as \( K = \varvec{xx}^{\text{T}} \). In order to solve conveniently, we defined

$$ {\varvec{\upalpha}} = (\lambda I_{N} + {\mathbf{K}})^{ - 1} {\mathbf{y}} $$
(5)

We get

$$ {\hat{\mathbf{w}}} = {\mathbf{x}}^{T} {\varvec{\upalpha}} = \sum\limits_{i = 1}^{N} {{\varvec{\upalpha}}_{i} {\mathbf{x}}_{i} } $$
(6)

After getting new candidate \( {\mathbf{x}}' \), using the model discussed above, the responding vector of all positions is given by

$$ {\hat{\mathbf{y}}} = {\hat{\mathbf{w}}}^{T} {\mathbf{x^{\prime}}} = \sum\limits_{i = 1}^{N} {\alpha_{i} {\mathbf{x}}_{{^{{_{i} }} }}^{T} {\mathbf{x^{\prime}}} = } \sum\limits_{i = 1}^{N} {\alpha_{i} \kappa ({\mathbf{x}}_{{^{i} }}^{{}} ,{\mathbf{x^{\prime}}})} $$
(7)

2.2 The Circulate Convolution in Kernel Space

The convolution of two vectors is defined as

$$ \varvec{p}*\varvec{q} = \sum\limits_{i} {\varvec{p}_{i} \varvec{q}_{\tau - i} } $$
(8)

Where vectors are \( \varvec{p} \in R^{\text{M}} \) and \( \varvec{q} \in R^{\text{N}} \), and the result is a \( (M + N + 1) \times 1 \) vector.

We can transform convolution to product by constructing circulate matrix:

$$ \varvec{p^{\prime}} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {p_{i} ,} & i \\ \end{array} \le {\text{M}}} \\ {\begin{array}{*{20}c} {0,} & {{\text{M}} < i \le {\text{N + M}} - 1} \\ \end{array} } \\ \end{array} } \right. $$
(9)
$$ \varvec{q^{\prime}} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {q_{i} ,} & i \\ \end{array} \le {\text{N}}} \\ {\begin{array}{*{20}c} {0,} & {{\text{N}} < i \le {\text{N + M}} - 1} \\ \end{array} } \\ \end{array} } \right. $$
(10)
$$ C(\varvec{p^{\prime}})\varvec{q^{\prime}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {p_{1}^{\prime } } & {p^{\prime}_{{{\text{M}} + {\text{N}} - 1}} } & \cdots & {p_{2}^{\prime } } \\ {p_{ 2}^{\prime } } & {p_{1}^{\prime } } & \cdots & {p_{3}^{\prime } } \\ \vdots & \vdots & \ddots & \vdots \\ {p^{\prime}_{{{\text{M}} + {\text{N}} - 1}} } & {p^{\prime}_{{{\text{M}} + {\text{N}} - 2}} } & \cdots & {p_{1}^{\prime } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ \vdots \\ 0 \\ \end{array} } \right] $$
(11)

According to convolution theorem, we can get:

$$ C(\varvec{p^{\prime}})\varvec{q^{\prime}} = F^{ - 1} (F(\varvec{p^{\prime}})F(\varvec{q^{\prime}})) $$
(12)

Given a single image \( X \), expressed as a \( n \times 1 \) vector \( x \). A \( n \times n \) circulate matrix \( C(\varvec{x}) \) is obtained:

$$ C(\varvec{x}) = \left[ {\begin{array}{*{20}c} {{\text{E}}_{0} \varvec{x}} & {{\text{E}}_{1} \varvec{x}} & \cdots & {{\text{E}}_{n - 1} \varvec{x}} \\ \end{array} } \right] $$
(13)

Where \( {\text{E}}_{i} \) is the permutation matrix that cyclically shifts \( x \) by \( i \).

$$ {\mathbf{E}}_{i} = \left[ {\begin{array}{*{20}c} {\overbrace {{\begin{array}{*{20}c} 0 & \cdots & 0 \\ \end{array} }}^{i}} & {\begin{array}{*{20}c} 1 & \cdots \\ \end{array} } & 0 \\ {\begin{array}{*{20}c} \vdots & \vdots & \vdots \\ \end{array} } & {\begin{array}{*{20}c} \vdots & \vdots \\ \end{array} } & \vdots \\ {\begin{array}{*{20}c} 0 & \cdots & 1 \\ \end{array} } & {\begin{array}{*{20}c} 0 & \cdots \\ \end{array} } & 0 \\ \end{array} } \right]_{{{\text{n}} \times {\text{n}}}} $$
(14)

The matrix \( {\mathbf{K}} \) with elements \( {\mathbf{K}}_{ij} = \kappa ({\text{E}}_{i} \varvec{x},{\text{E}}_{j} \varvec{x}) \) which is composed with elements of \( C(\varvec{x}) \) is circulate [9]. We will define \( {\mathbf{K}} \) with Gaussian kernel and the convolution of kernel space is compute as

$$ \begin{aligned} {\mathbf{k}}_{i}^{gauss} & = \kappa (\varvec{x^{\prime}},{\text{E}}_{i} \varvec{x}) \\ & = \exp ( - \frac{{||\varvec{x^{\prime}}||^{2} + ||\varvec{x}||^{2} - 2\varvec{x^{\prime}}^{\text{T}} {\text{E}}_{i} \varvec{x}}}{{2\delta^{2} }}) \\ \end{aligned} $$
(15)

As \( {\text{E}}_{i} \) is the permutation matrix, kernel function is given by

$$ \begin{aligned} {\mathbf{k}}^{gauss} & = \exp ( - \frac{{||\varvec{x}||^{2} + ||\varvec{x^{\prime}}||^{2} - 2C(\varvec{x}')\varvec{x}}}{{2\delta^{2} }}) \\ & = \exp ( - \frac{{||\varvec{x}||^{2} + ||\varvec{x^{\prime}}||^{2} - 2F^{ - 1} (F(\varvec{x^{\prime}})F(\varvec{x}))}}{{2\delta^{2} }}) \\ \end{aligned} $$
(16)

We can transform Eq. (5) into frequency domains

$$ {\varvec{\upalpha}} = (\lambda I_{N} + {\mathbf{K}})^{ - 1} {\mathbf{y}} = F^{ - 1} (\frac{{F({\mathbf{y}})}}{{F({\mathbf{K}}) + \lambda }}) $$
(17)

Equation (7) is computed as

$$ {\hat{\mathbf{y}}} = F^{ - 1} (F({\mathbf{K}})F({\varvec{\upalpha}})) $$
(18)

We will get the object location which is corresponding to the best response.

3 Scale Theory

3.1 Mean Shift Algorithm Theory

The mean shift algorithm was widely used in visual tracking. The basic idea is that Bhattacharyya coefficient and other information-theoretic similarity measures are employed to measure the similarity between the target model and the current target region. Generally, the model is represented by normalized histogram vector.

The normalized pixels are denoted by \( \{ x_{i} \}_{i = 1,2, \ldots ,n} \) in the target region, which has n pixels. The probability of a feature \( u \), which is actually one of the m color histogram bins. The target model is computed as

$$ \varvec{q}_{u} = C\sum\limits_{i = 1}^{n} {k(\left\| {x_{i}^{ * } } \right\|^{2} )} \delta [b(x_{i}^{ * } ) - u] $$
(19)

Where, \( b_{f} :R^{2} \to \{ 1, \cdots ,m\} \) associates the pixels \( x_{0} \) to the histogram bin, \( k() \) is an isotropic kernel profile and is \( \delta \) the Kronecker delta function, Constant \( C \) is an normalization about \( \sum\limits_{u = 1}^{m} {q{}_{u}} = 1 \).

Similarity, the probability of feature in the candidate target model is given by

$$ \varvec{p}_{u} (y) = C_{h} \sum\limits_{i = 1}^{{n_{h} }} {k(\left\| {\frac{{y - x_{i} }}{h}} \right\|^{2} )} \delta [b(x_{i} ) - u] $$
(20)

Where \( y \) is the center of the target candidate region.

The similarity between target model and candidate target model is measured by Bhattacharyya coefficient which is given by

$$ \rho (y) \equiv \rho [\varvec{p}_{u} (y),\varvec{q}_{u} ] = \sum\limits_{u = 1}^{m} {\sqrt {\varvec{p}_{u} (y)\varvec{q}_{u} } } $$
(21)

In order to find the best location of the object, a key procedure is the computation of an offset form current location \( y_{0} \) to the new location \( y_{1} \) according to the iteration equation:

$$ y_{1} = \frac{{\sum\limits_{i = 1}^{{n_{h} }} {x_{i} w_{i} g\left( {\left\| {(y_{0} - x_{i} )/h} \right\|^{2} } \right)} }}{{\sum\limits_{i = 1}^{{n_{h} }} {w_{i} g\left( {\left\| {(y_{0} - x_{i} )/h} \right\|^{2} } \right)} }} $$
(22)

Where, \( w_{i} = \sum\limits_{u = 1}^{m} {\sqrt {\frac{{q_{u} }}{{p_{u} (y_{0} )}}} } \sigma \left[ {b\left( {x_{i} } \right) - u} \right],g(x) = - k'(x) \)

3.2 Estimates the Best Scale of the Object

In this section, we will propose a convenient algorithm which is based on [11] to estimate the best scale of the object. The algorithm can precisely estimate object’s scale by utilising the zeroth-order moment of the weight image of all pixels in the target candidate region and the similarity between target model and target candidate model.

The changing of target is usually a gradual process in the sequential frames. Thus we can assume that the changing of target’s scale and location is smooth and this assumption owes reasonably well in most video sequences. With the assumption, we will track the target in a larger candidate region than its size to ensure that the target is in this candidate region based on the area of the target in the previous frame. The weight image is defined as computing the weight of every pixels, which is the square root of the ratio of its colour probability in the target model to its colour probability in the target candidate model. For a pixel \( x_{i} \) in the target candidate region, its weight is given by

$$ w_{i} = \sum\limits_{u = 1}^{m} {\sqrt {\frac{{q_{u} }}{{p_{u} (y_{0} )}}} } \sigma \left[ {b\left( {x_{i} } \right) - u} \right] $$
(23)

The weight value of every pixel represents the possibility that it belongs to the object. So the weight image can be regarded as the density distribution function of the object in the target candidate region. Figure 1 shows the weight image of target candidate region with different scale of target.

Fig. 1.
figure 1

The weight image of target candidate region with different scale of target

Full size image

Figure 1a shows a target consisted with four grey levels. Figure 1b represents the candidate region that is larger than the target. Figure 1c, e, g and d, f, h respectively illustrate the target candidate region with different scale of object and corresponding weight images calculated by our algorithm.

Form Fig. 1, we can see clearly that the weight image will change dynamically with the changing of object’s scale. Particularly, the weight image is closely related to the object’s change. The closer the real scale of the object is to the candidate region, the better the weight approaches to 1. Based on those properties, the sum of the weights of all pixels, that is, the zeroth-order moment is considered as the predetermination which reflect the scale of the target.

$$ \text{M}_{0} = \sum\limits_{i = 1}^{n} {w\left( {x_{i} } \right)} $$
(24)

However, owing to the existence of the background pixels, the probability of the target features is less than that in the target model. So (23) will enlarge the weights of target pixels and restrain the weights of background pixels. Thus, the target pixels will contribute more to target area estimation, whereas the background pixels contribute less. This can be seen in Fig. 1d, f and h. On the other hand, the Bhattacharyya coefficient is used to represent the similarity between the target model and the target candidate model. A smaller Bhattacharyya coefficient means that there are more background features and fewer target features in the target candidate region. If we use \( \text{M}_{0} \) as the estimation of the target area, then according to (24), when the weights form the target become bigger, the estimation error by using \( \text{M}_{0} \) as the evaluation of target scale will be bigger, vice versa. Therefore, the Bhattacharyya coefficient is a good indicator of how reliable it is by using \( \text{M}_{0} \) as the target area. That is to say, with the increase of the Bhattacharyya coefficient, the estimation accuracy will also increase. So the Bhattacharyya coefficient is used to adjust \( \text{M}_{0} \) in estimating the target area. The estimating equation is

$$ {\text{A}} = c\left( \rho \right)\text{M}_{0} $$
(25)

Where, \( c\left( \rho \right) \) is a monotonically increasing function with respect to the Bhattacharyya coefficient \( \rho \left( {0 \le \rho \le 1} \right) \). \( c\left( \rho \right) \) is defined as

$$ c\left( \rho \right) = \exp \left( {\frac{\rho - 1}{{\sigma_{1} }}} \right) $$
(26)

where \( \sigma_{1} \) is a constant. From (25) and (26), we can get that when the target candidate model approaches to the target model, that is, when \( \rho \) approaches to 1, \( c\left( \rho \right) \) approaches to 1 and in this case it is reliable to use \( \text{M}_{0} \) as the estimation of target scale. When the candidate model is not identical to the target model, that is, when \( \rho \) decreases, \( \text{M}_{0} \) will be much bigger than the target scale, but \( c\left( \rho \right) \) is less than 1. So \( {\text{A}} \) can avoid being biased too much from the real target scale. The experiment show that setting \( \sigma_{1} \) between 1 and 2 can achieve accurate estimation of target scale [11].

In this paper, target’s state is showed by rectangle and the ratio of length to wide is constant \( {\rm K} \). With the estimation of target scale, the length and wide of target is given by

$$ h = \sqrt {\text{KA}} ,w = \sqrt {{\raise0.7ex\hbox{${\text{A}}$} \!\mathord{\left/ {\vphantom {{\text{A}} {\text{K}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{K}}$}}} $$
(27)

4 Model Update Strategy

Model update is an important step in visual tracking, which is help to avoid the drifting of model. In order to adapt the change of target and alleviate the interference of background, we update the regression model and histogram model of target.

Regression Model Update:

The target’s regression model is updated every frame by combining the fixed reference model extracted from previous frame and the result form the most recent frame with an update weight \( \beta \). The update equation is

$$ \hat{\varvec{w}}_{new} = \beta \hat{\varvec{w}}_{cur} + (1 - \beta )\hat{\varvec{w}}_{old} $$
(28)

Where \( \hat{\varvec{w}}_{new} \) is new model, \( \hat{\varvec{w}}_{old} \) is the old model used by last frame, \( \hat{\varvec{w}}_{cur} \) is the current model obtained from current frame.

Histogram Model Update:

We set a threshold \( \rho ' \) for the target’s histogram model update. Then we analyze the Bhattacharyya coefficient to determine when to update the histogram model:

  1. (1)

    if \( \rho \ge \rho ' \), the target’s histogram have no significant changes, so don’t update the histogram model.

  2. (2)

    if \( \rho < \rho ' \), the target’s histogram may changes greatly, so we update the histogram model with a update weight \( \alpha \). The update equation is

    $$ q_{u(new)} = \alpha p_{u(cur)} + (1 - \alpha )q_{u(old)} $$
    (29)

Where \( q_{u(new)} \) is the new histogram, \( q_{u(old)} \) is the previous histogram model, \( p_{u(cur)} \) is the current histogram model obtained from current frame.

5 The Proposed Algorithm

5.1 The Basic Theory

In order to improve robustness of tracking algorithm, we propose a scale adaptive tracking algorithm based on kernel ridge regression and Fast Fourier Transform. Firstly, the algorithm establish regression model and search object’s location using regression model. Secondly, the paper presents a method that estimates the best scale of target by considering the weight image.

5.2 Algorithm Step

The proposed tracking algorithm is summarized as follows:

Step 1::

Initialize the target’s state and obtain the training data. Calculate the regression model by (6) and (17) and the target histogram model \( \varvec{q}_{u} \) by (19)

Step 2::

Search object’s location \( \hat{y} \) by (18)

Step 3::

Calculate the target candidate histogram model \( \varvec{p}_{u} (\hat{y}) \) by (20) and the Bhattacharyya coefficient \( \rho \) by (21)

Step 4::

Calculate the weight image of the candidate region by (23)

Step 5::

Estimates the best scale \( {\text{A}} \) of target by (25) and Calculate the length \( h \) and wide \( w \) by (28). Then get the tracking result of current frame

Step 6::

Calculate the regression model with new training data and update the regression model by (28)

Step 7::

Synthetically analyze the Bhattacharyya coefficient \( \rho \) and threshold \( \rho ' \), determine if it is necessary to update the histogram model by (29), and continue the tracking for the next frame

5.3 Algorithm Flow

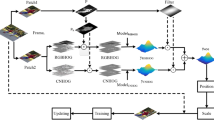
The whole flow chart is presented in Fig. 2.

Fig. 2.
figure 2

Flow chart of the our tacking algorithm

Full size image

6 Experimental Results and Discussions

Several representative sequences are used to compare the proposed algorithm (Ours) with the kernel-based tracker (KBT) [4], the CBWH [9] based on corrected background-weighted histogram, the DFT [8] based on distribution fields and the DSSM [6] based on discriminative sparse similarity map. For all the sequences, we select a four times bigger region centered with the object as the candidate region of our algorithm. The regularization parameter \( \lambda \) is set at 0.01. The update weight \( \beta \) of regression model is set at 0.075 and the update weight \( \alpha \) of histogram model is set at 0.1. Note that both of \( \alpha \) and \( \beta \) is getting from experiences. The experimental experiences show that setting scale factor \( \sigma_{1} \) between 1 and 2 can achieve accurate estimation of target scale. All the experiments are implemented under the 2.6 GHz PC with 2 GB memory and the programming environment is MATLAB R2009a.

The first experiment is on the singer sequence, which has obviously scale shrinking and the interference of background. Figure 3(a) shows the tracking results of the sequences. We can see, as the background interference, KBT and DFT have large tracking error in the frame of 192 and 262. CBWH can decrease the distraction of background, but with the algorithm can’t adapt the changes of target’s scale, tracking result is also bad. Although DSSM can track target successfully, our algorithm has better result in estimating target’s location and adapting the changing of target’ scale (263 and 309 frame).

Fig. 3.
figure 3

Qualitative comparison of the tracking algorithms

Full size image

The second experiment is a challenging video sequence, which has acutely scale enlarging, pose changing and local shelter. Figure 3(b) shows the tracking results of the sequences. Since CBWH and DFT lack necessary scale adapt mechanism, they can’t adapt the obvious change of scale. KBT and DSSM have large tracking error after target’s pose changing obviously along with acutely enlarging of scale (182 and 252 frame). While our tracking algorithm can get the target location and scale with acceptable precision.

The third video is the Trellis sequence. In this video sequence, complicated background interference and scale changing are the major challenge. The tracking results is showed in Fig. 3(c). Along with the scale changing of target, the background distracts severely, and both KBT, DFT and CBWH have obviously tracking deviation. DSSM and our algorithm can track target successfully.

In order to quantitatively analyse the real-time performance of our algorithm and referenced algorithms, we use the average running time to compare the efficiency in the above video sequences. Table 1 shows the comparison results of the average running time of per frame, which is get by running all the algorithms with same configuration and using the same dataset for fair comparison. The results proves that the proposed algorithm is best in real-time performance.

Table 1. Average running time of per frame
Full size table

In order to analyse the performance of tracking accuracy, we use the center location error and overlap to compare the accuracy in the above video sequences. It should be noted that a smaller center location error and a bigger overlap rate implies a more accurate result. The center location error is the Euclidean distance between center location and the ground truth. Figure 4 shows the center location error curves of the trackers. The overlap rate reflects the covering level of tracking result and the corresponding ground truth. The overlap rate curves of our algorithm and compared algorithms is showed in Fig. 5. Tables 2 and 3 shows the average center location errors and the average overlap rates respectively. As shown in the table, the proposed algorithm exceeds the referenced algorithms.

Fig. 4.
figure 4

Center location error curves

Full size image
Fig. 5.
figure 5

Overlap rate curves

Full size image
Table 2. Average center location error
Full size table
Table 3. Average overlap rate
Full size table

7 Conclusions

In conclusion, for the drawback of traditional regression tracking algorithm, we proposed a scale adaptive tracking algorithm, which build target’s model based on kernel ridge regression and evaluate target’s scale using weight image. First, the algorithm establish regression model and get object’s location in the search region using regression model. In order to improve the tracking efficiency, we transform the operations of time domain into frequency domain by using Fast Fourier Transform. Second, the paper present a method that estimates the best scale of target by considering the weight image of all pixels in the candidate region. The experimental results and quantitative evaluation demonstrate that the proposed algorithm owns good accuracy and efficiency.