Abstract
We introduce cellular automata whose cell spaces are left homogeneous spaces and prove a uniform as well as a topological variant of the Curtis-Hedlund-Lyndon theorem. Examples of left homogeneous spaces are spheres, Euclidean spaces, as well as hyperbolic spaces acted on by isometries; vertex-transitive graphs, in particular, Cayley graphs, acted on by automorphisms; groups acting on themselves by multiplication; and integer lattices acted on by translations.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
In the first chapter of the monograph ‘Cellular Automata and Groups’ [1], Tullio Ceccherini-Silberstein and Michel Coornaert develop the theory of cellular automata whose cell spaces are groups. Examples of groups are abound: The integer lattices and Euclidean spaces with addition (translation), the one-dimensional unit sphere embedded in the complex plane with complex multiplication (rotation), and the vertices of a Cayley graph with the group structure it encodes (graph automorphisms).
Yet, there are many structured sets that do not admit a structure-preserving group structure. For example: Each Euclidean n-sphere, except for the zero-, one-, and three-dimensional, does not admit a topological group structure; the Petersen graph is not a Cayley graph and does thus not admit an edge-preserving group structure on its vertices. However, these structured sets can be acted on by subgroups of their automorphism group by function application. For example Euclidean n-spheres can be acted on by rotations about the origin and graphs can be acted on by edge-preserving permutations of their vertices.
Moreover, there are structured groups that have more symmetries than can be expressed with the group structure. The integer lattices and the Euclidean spaces with addition, for example, are groups, but addition expresses only their translational symmetries and not their rotational and reflectional ones. Though, they can be acted on by arbitrary subgroups of their symmetry groups, like the ones generated by translations and rotations.
The general notion that encompasses these structure-preserving actions is that of a group set, that is, a set that is acted on by a group. A group set M acted on by G such that for each tuple \((m, m') \in M \times M\) there is a symmetry \(g \in G\) that transports m to \(m'\) is called left homogeneous space and the action of G on M is said to be transitive. In particular, groups are left homogeneous spaces — they act on themselves on the left by multiplication.
In this paper, we develop the theory of cellular automata whose cell spaces are left homogeneous spaces which culminates in the proof of a uniform and topological variant of a famous theorem by Morton Landers Curtis, Gustav Arnold Hedlund, and Roger Conant Lyndon from 1969, see the paper ‘Endomorphisms and automorphisms of the shift dynamical system’ [2]. The development of this theory is greatly inspired by [1].
These cellular automata are defined so that their global transition functions are equivariant under the induced group action on global configurations. Depending on the choice of the cell space, these actions may be plain translations but also rotations and reflections. Exemplary for the first case are integer lattices that are acted on by translations; and for the second case Euclidean n-spheres that are acted on by rotations, but also the two-dimensional integer lattice that is acted on by the group generated by translations and the rotation by \(90^\circ \).
Sébastien Moriceau defines and studies a more restricted notion of cellular automata over group sets in his paper ‘Cellular Automata on a G-Set’ [3]. He requires sets of states and neighbourhoods to be finite. His automata are the global transition functions of, what we call, semi-cellular automata with finite set of states and finite essential neighbourhood.
His automata obtain the next state of a cell by shifting the global configuration such that the cell is moved to the origin, restricting that configuration to the neighbourhood of the origin, and applying the local transition function to that local configuration. Our automata obtain the next state of a cell by determining the neighbours of the cell, observing the states of that neighbours, and applying the local transition function to that observed local configuration. The results are the same but the viewpoints are different, which manifests itself in proofs and constructions.
To determine the neighbourhood of a cell we let the relative neighbourhood semi-act on the right on the cell. That right semi-action is to the left group action what right multiplication is to the corresponding left group multiplication. Many properties of cellular automata are a consequence of the interplay between properties of that semi-action, shifts of global configurations, and rotations of local configurations. That semi-action also plays an important role in our definition of right amenable left group sets, see [4], for which the Garden of Eden theorem holds, see [5], which states that each cellular automaton is surjective if and only if it is pre-injective. For example finitely right generated left homogeneous spaces of sub-exponential growth are right amenable, in particular, quotients of finitely generated groups of sub-exponential growth by finite subgroups acted on by left multiplication.
In Sect. 1 we introduce left group actions and our prime example, which illustrates phenomena that cannot be encountered in groups acting on themselves on the left by multiplication. In Sect. 2 we introduce coordinate systems, cell spaces, and right quotient set semi-actions that are induced by left group actions and coordinate systems. In Sect. 3 we introduce semi-cellular and cellular automata. In Sect. 4 we show that a global transition function does not depend on the choice of coordinate system, is equivariant under the induced left group action on global configurations, is determined by its behaviour in the origin, and that the composition of two global transition functions is a global transition function. In Sect. 5 we prove a uniform and a topological variant of the Curtis-Hedlund-Lyndon theorem, which characterise global transition functions of semi-cellular automata by uniform and topological properties respectively. And in Sect. 6 we characterise invertibility of semi-cellular automata.
1 Left Group Actions
Definition 1
Let M be a set, let G be a group, let \(\triangleright \) be a map from \(G \times M\) to M, and let \(e_G\) be the neutral element of G. The map \(\triangleright \) is called left group action of G on M, the group G is said to act on M on the left by \(\triangleright \), and the triple \(({M, G, \triangleright })\) is called left group set if and only if

Example 1
Let G be a group. It acts on itself on the left by \(\triangleright \) by multiplication.
Example 2
Let M be the Euclidean unit 2-sphere, that is, the surface of the ball of radius 1 in 3-dimensional Euclidean space, and let G be the rotation group. The group G acts on M on the left by \(\triangleright \) by function application, that is, by rotation about the origin.
Definition 2
Let \(\triangleright \) be a left group action of G on M and let H be a subgroup of G. The left group action \(\triangleright \mathord {\upharpoonright }_{H \times M}\) of H on M is denoted by \(\triangleright _H\).
Definition 3
Let \(\triangleright \) be a left group action of G on M. It is called
-
1.
transitive if and only if the set M is non-empty and

-
2.
free if and only if
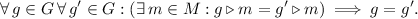
Example 3
In the situation of Example 1, the left group action is transitive and free.
Example 4
In the situation of Example 2, the left group action is transitive but not free.
Definition 4
Let \(( M, G, \triangleright )\) be a left group set. It is called left homogeneous space if and only if the left group action \(\triangleright \) is transitive.
Definition 5
Let \(\triangleright \) be a left group action of G on M, and let m and \(m'\) be two elements of M.
-
1.
The set \(G \triangleright m = \{g \triangleright m \mid g \in G\}\) is called orbit of m under \(\triangleright \).
-
2.
The set \(G_m = \{g \in G \mid g \triangleright m = m\}\) is called stabiliser of m under \(\triangleright \).
-
3.
The set \(G_{m,m'} = \{g \in G \mid g \triangleright m = m'\}\) is called transporter of m to \(m'\) under \(\triangleright \).
Example 5
In the situation of Example 3, each orbit is G and each stabiliser is \(\{e_G\}\).
Example 6
In the situation of Example 4, for each point \(m \in M\), its orbit is M and its stabiliser is the group of rotations about the line through the origin and itself.
Lemma 1
Let \(\triangleright \) be a left group action of G on M, let m and \(m'\) be two elements of M that have the same orbit under \(\triangleright \), and let g be an element of \(G_{m,m'}\). Then, \(G_{m'} = g G_m g^{-1}\) and \(g G_m = G_{m,m'} = G_{m'} g\). \(\square \)
Definition 6
Let M and \(M'\) be two sets, let f be a map from M to \(M'\), and let \(\triangleright \) be a left group action of G on M. The map f is called \(\triangleright \)-invariant if and only if

Definition 7
Let M and \(M'\) be two sets, let f be a map from M to \(M'\), and let \(\triangleright \) and \(\triangleright '\) be two left group actions of G on M and \(M'\) respectively. The map f is called \((\triangleright , \triangleright ')\) -equivariant if and only if

and \(\triangleright \) -equivariant if and only if it is \((\triangleright , \triangleright ')\)-equivariant, \(M = M'\), and \(\triangleright = \triangleright '\).
Lemma 2
Let f be a \((\triangleright , \triangleright ')\)-equivariant and bijective map from M to \(M'\). The inverse of f is \((\triangleright ', \triangleright )\)-equivariant
Lemma 3
Let G be a group and let H be a subgroup of G. The group G acts transitively on the quotient set \(G \slash H\) on the left by
Lemma 4
Let \(\triangleright \) be a transitive left group action of G on M, let \(m_0\) be an element of M, and let \(G_0\) be the stabiliser of \(m_0\) under \(\triangleright \). The map
is \((\triangleright , \cdot )\)-equivariant and bijective.
2 Right Quotient Set Semi-Actions
Definition 8
Let \(\mathcal {M} = ( M, G, \triangleright )\) be a left homogeneous space, let \(m_0\) be an element of M, let \(g_{m_0, m_0}\) be the neutral element of G, and, for each element \(m \in M \setminus \{m_0\}\), let \(g_{m_0, m}\) be an element of G such that \(g_{m_0, m} \triangleright m_0 = m\). The tuple  is called coordinate system for \(\mathcal {M}\); the element \(m_0\) is called origin; for each element \(m \in M\), the element \(g_{m_0, m}\) is called coordinate of m; for each subgroup H of G, the stabiliser of the origin \(m_0\) under \(\triangleright _H\), which is \(G_{m_0} \cap H\), is denoted by \(H_0\).
is called coordinate system for \(\mathcal {M}\); the element \(m_0\) is called origin; for each element \(m \in M\), the element \(g_{m_0, m}\) is called coordinate of m; for each subgroup H of G, the stabiliser of the origin \(m_0\) under \(\triangleright _H\), which is \(G_{m_0} \cap H\), is denoted by \(H_0\).
Definition 9
Let \(\mathcal {M} = ( M, G, \triangleright )\) be a left homogeneous space and let  be a coordinate system for \(\mathcal {M}\). The tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is called cell space, each element \(m \in M\) is called cell, and each element \(g \in G\) is called symmetry.
be a coordinate system for \(\mathcal {M}\). The tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is called cell space, each element \(m \in M\) is called cell, and each element \(g \in G\) is called symmetry.
Example 7
In the situation of Example 5, let \(m_0\) be the neutral element \(e_G\) of G and, for each element \(m \in G\), let \(g_{m_0, m}\) be the only element in G such that \(g_{m_0, m} m_0 = m\), namely m. The tuple  is a coordinate system of \(\mathcal {M} = ( G, G, \cdot )\) and the tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is a cell space.
is a coordinate system of \(\mathcal {M} = ( G, G, \cdot )\) and the tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is a cell space.
Example 8
In the situation of Example 6, let \(m_0\) be the north pole \((0,0,1)^\intercal \) of M and, for each point \(m \in M\), let \(g_{m_0, m}\) be a rotation about an axis in the (x, y)-plane that rotates \(m_0\) to m. Note that \(g_{m_0, m_0}\) is the trivial rotation. The tuple  is a coordinate system of \(\mathcal {M} = ( M, G, \triangleright )\) and the tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is a cell space.
is a coordinate system of \(\mathcal {M} = ( M, G, \triangleright )\) and the tuple \(\mathcal {R} = ( \mathcal {M}, \mathcal {K})\) is a cell space.
In the remainder of this section, let  be a cell space.
be a cell space.
Lemma 5
The map

is a right quotient set semi-action of \(G \slash G_0\) on M with defect \(G_0\), which means that, for each subgroup H of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\),

Example 9
In the situation of Example 7, the stabiliser \(G_0\) of the neutral element \(m_0\) under \(\cdot \) is the trivial subgroup \(\{e_G\}\) of G and, for each element \(g \in G\), we have \(g_{m_0, m} g g_{m_0, m}^{-1} m = m g m^{-1} m = m g\). Under the natural identification of \(G \slash G_0\) with G, the induced semi-action  is the right group action of G on itself by multiplication.
is the right group action of G on itself by multiplication.
Example 10
In the situation of Example 8, the stabiliser \(G_0\) of the north pole \(m_0\) under \(\triangleright \) is the group of rotations about the z-axis. An element \(g G_0 \in G \slash G_0\) semi-acts on a point m on the right by the induced semi-action  by first rotating m to \(m_0\), \(g_{m_0, m}^{-1} \triangleright m = m_0\), secondly rotating \(m_0\) as prescribed by g, \(g g_{m_0, m}^{-1} \triangleright m = g \triangleright m_0\), and thirdly undoing the first rotation, \(g_{m_0, m} g g_{m_0, m}^{-1} \triangleright m = g_{m_0, m} \triangleright (g \triangleright m_0)\), in other words, by first changing the rotation axis of g such that the new axis stands to the line through the origin and m as the old one stood to the line through the origin and \(m_0\), \(g_{m_0, m} g g_{m_0, m}^{-1}\), and secondly rotating m as prescribed by this new rotation.
by first rotating m to \(m_0\), \(g_{m_0, m}^{-1} \triangleright m = m_0\), secondly rotating \(m_0\) as prescribed by g, \(g g_{m_0, m}^{-1} \triangleright m = g \triangleright m_0\), and thirdly undoing the first rotation, \(g_{m_0, m} g g_{m_0, m}^{-1} \triangleright m = g_{m_0, m} \triangleright (g \triangleright m_0)\), in other words, by first changing the rotation axis of g such that the new axis stands to the line through the origin and m as the old one stood to the line through the origin and \(m_0\), \(g_{m_0, m} g g_{m_0, m}^{-1}\), and secondly rotating m as prescribed by this new rotation.
Let \(N_0\) be a subset of the sphere M, which we think of as a geometrical object on the sphere that has its centre at \(m_0\), for example, a circle of latitude. The set \(N = \{g G_0 \in G \slash G_0 \mid g \triangleright m_0 \in N_0\} = \{G_{m_0, m} \mid m \in N_0\} = \{g_{m_0, m} G_0 \mid m \in N_0\}\) can be thought of as a realisation of \(N_0\) in \(G \slash G_0\). Indeed,  . Furthermore, for each point \(m \in M\), the set
. Furthermore, for each point \(m \in M\), the set  has the same shape and size as \(N_0\) but its centre at m.
has the same shape and size as \(N_0\) but its centre at m.
Lemma 6
The semi-action  is
is
-
1.
transitive, which means that the set M is non-empty and

-
2.
free, which means that
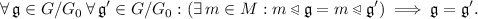
Lemma 7
The semi-action 
-
1.
semi-commutes with \(\triangleright \), which means that, for each subgroup H of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\),
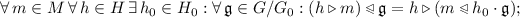
-
2.
exhausts its defect with respect to its semi-commutativity with \(\triangleright \) in \(m_0\), which means that, for each subgroup H of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\),

Lemma 8
The maps

are inverse to each other and, under the identification of \(G \slash G_0\) with M by either of these maps,

3 Semi-Cellular and Cellular Automata
In this section, let \(\mathcal {R} = ( \mathcal {M}, \mathcal {K}) = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space.
Definition 10
Let Q be a set, let N be a subset of \(G \slash G_0\) such that \(G_0 \cdot N \subseteq N\), and let \(\delta \) be a map from \(Q^N\) to Q. The quadruple \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) is called semi-cellular automaton, each element \(q \in Q\) is called state, the set N is called neighbourhood, each element \(n \in N\) is called neighbour, and the map \(\delta \) is called local transition function.
Example 11
In the situation of Example 9, the semi-cellular automata over \(\mathcal {R}\) are the usual cellular automata over the group G.
Example 12
In the situation of Example 10, let Q be the set \(\{0,1\}\), let \(N_0\) be the union of all circles of latitude between \(45^\circ \) and \(90^\circ \) north, which is a curved circular disk of radius \(\pi /4\) with the north pole \(m_0\) at its centre, let N be the set \(\{g G_0 \mid g \triangleright m_0 \in N_0\}\), and let
The quadruple \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) is a semi-cellular automaton.
In the remainder of this section, let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton.
Definition 11
Let E be a subset of N. It is called essential neighbourhood if and only if

Definition 12
Each map \(\ell \in Q^N\) is called local configuration. The stabiliser \(G_0\) acts on \(Q^N\) on the left by
Definition 13
The semi-cellular automaton \(\mathcal {C}\) is called cellular automaton if and only if its local transition function \(\delta \) is \(\bullet \)-invariant.
Example 13
In the situation of Example 11, the stabiliser \(G_0\) of the neutral element \(m_0\) is the trivial subgroup \(\{e_G\}\) of G. Therefore, for each semi-cellular automaton over \(\mathcal {R}\), its local transition function is \(\bullet \)-invariant and hence it is a cellular automaton.
Example 14
In the situation of Example 12, think of 0 as black, 1 as white, and of local configurations as black-and-white patterns on  . The rotations \(G_0\) about the z-axis act on these patterns by \(\bullet \) by rotating them. The local transition function \(\delta \) maps the black pattern to 0 and all others to 1, which is invariant under rotations. Therefore, the quadruple \(\mathcal {C}\) is a cellular automaton.
. The rotations \(G_0\) about the z-axis act on these patterns by \(\bullet \) by rotating them. The local transition function \(\delta \) maps the black pattern to 0 and all others to 1, which is invariant under rotations. Therefore, the quadruple \(\mathcal {C}\) is a cellular automaton.
Definition 14
Each map \(c \in Q^M\) is called global configuration. The group G acts on \(Q^M\) on the left by

Definition 15
For each global configuration \(c \in Q^M\) and each cell \(m \in M\), the local configuration

is called observed by m in c.
Remark 1
Because the semi-action  is free, for each local configuration \(\ell \in Q^N\) and each cell \(m \in M\), there is a global configuration \(c \in Q^M\) such that the local configuration observed by m in c is \(\ell \).
is free, for each local configuration \(\ell \in Q^N\) and each cell \(m \in M\), there is a global configuration \(c \in Q^M\) such that the local configuration observed by m in c is \(\ell \).
Definition 16
The map

is called global transition function.
Example 15
In the situation of Example 14, repeated applications of the global transition function of \(\mathcal {C}\) grows white regions on M.
Remark 2
For each subset A of M and each global configuration \(c \in Q^M\), the states of the cells A in \(\varDelta (c)\) depends at most on the states of the cells  in c. More precisely,
in c. More precisely,

Lemma 9
Let m be an element of M, let g be an element of G, and let \(g_0\) be an element of \(G_0\) such that

For each global configuration \(c \in Q^M\),

Definition 17
The set  is called neighbourhood of \(m_0\).
is called neighbourhood of \(m_0\).
Definition 18
The map

is called local transition function of \(m_0\).
Lemma 10
The global transition function \(\varDelta \) of \(\mathcal {C}\) is identical to the map

4 Invariance, Equivariance, Determination, and Composition of Global Transition Functions
In Theorem 1 we show that a global transition function does not depend on the choice of coordinate system. In Theorem 2 we show that a global transition function is  -equivariant if and only if the local transition function is \(\bullet \)-invariant. In Theorem 3 we show that a global transition function is determined by its behaviour in the origin. And in Theorem 4 we show that the composition of two global transition functions is a global transition function.
-equivariant if and only if the local transition function is \(\bullet \)-invariant. In Theorem 3 we show that a global transition function is determined by its behaviour in the origin. And in Theorem 4 we show that the composition of two global transition functions is a global transition function.
Lemma 11
Let \(\triangleright \) be a left group action of G on M. The group G acts on \(\bigcup _{m \in M} G \slash G_m\) on the left by
such that, for each element \(g \in G\) and each element \(m \in M\), the map

is bijective.
Lemma 12
Let \(\mathcal {M} = ( M, G, \triangleright )\) be a left homogeneous space, let \(\mathcal {K} = ( m_0, \{{g_{m_0, m}}\}_{m \in M})\) and \(\mathcal {K}' = ( m_0', \{{g_{m_0', m}'}\}_{m \in M})\) be two coordinate systems for \(\mathcal {M}\), let H be a subgroup of G such that \(\{g_{m_0, m\} \mid m \in M} \cup \{g_{m_0', m\}' \mid m \in M} \subseteq H\), and let h be an element of H such that \(h \triangleright m_0 = m_0'\). Then,

Theorem 1
In the situation of Lemma 12, let \(\mathcal {C} = ( ( \mathcal {M}, \mathcal {K}), Q, N, \delta )\) be a semi-cellular automaton such that \(\delta \) is \(\bullet _{H_0}\)-invariant, let \(N'\) be the set \(h \circ N\), and let
The quadruple \(( ( \mathcal {M}, \mathcal {K}'), Q, N', \delta ')\) is a semi-cellular automaton whose global transition function is identical to the one of \(\mathcal {C}\).
Corollary 1
Let \(( \mathcal {M}, \mathcal {K}) = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space and let \(\mathcal {C} = ( ( \mathcal {M}, \mathcal {K}), Q, N, \delta )\) be a cellular automaton. For each coordinate system \(\mathcal {K}' = ( m_0', \{{g_{m_0', m}'}\}_{m \in M})\) for \(\mathcal {M}\), there is a cellular automaton \(( ( \mathcal {M}, \mathcal {K}'), Q, N', \delta ')\) whose global transition function is identical to the one of \(\mathcal {C}\). \(\square \)
Theorem 2
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\).
-
1.
If the local transition function \(\delta \) is \(\bullet _{H_0}\)-invariant, then the global transition function \(\varDelta \) is
 -equivariant.
-equivariant. -
2.
If there is an
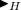 -equivariant map \(\varDelta _0 :Q^M \rightarrow Q^M\) such that
-equivariant map \(\varDelta _0 :Q^M \rightarrow Q^M\) such that 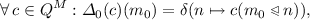 (1)
(1)then the local transition function \(\delta \) is \(\bullet _{H_0}\)-invariant.
-
3.
The local transition function \(\delta \) is \(\bullet _{H_0}\)-invariant if and only if the global transition function \(\varDelta \) is
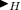 -equivariant.
-equivariant.
Corollary 2
Let \(\mathcal {C}\) be a semi-cellular automaton. It is a cellular automaton if and only if its global transition function is  -equivariant. \(\square \)
-equivariant. \(\square \)
Theorem 3
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton, let \(\varDelta _0\) be a map from \(Q^M\) to \(Q^M\), and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). The following statements are equivalent:
-
1.
The local transition function \(\delta \) is \(\bullet _{H_0}\)-invariant and the global transition function of \(\mathcal {C}\) is \(\varDelta _0\);
-
2.
The global transition function \(\varDelta _0\) is
 -equivariant and
-equivariant and 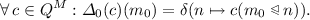 (2)
(2)
Theorem 4
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) and \(\mathcal {C}' = ( \mathcal {R}, Q, N', \delta ')\) be two semi-cellular automata, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\), and \(\delta \) and \(\delta '\) are \(\bullet _{H_0}\)-invariant. Furthermore, let
and let

The quadruple \(\mathcal {C}'' = ( \mathcal {R}, Q, N'', \delta '')\) is a semi-cellular automaton whose local transition function is \(\bullet _{H_0}\)-invariant and whose global transition function is \({\varDelta \circ \varDelta '}\).
5 Curtis-Hedlund-Lyndon Theorems
In this section we equip the the set of global configurations with a uniform and a topological structure, and prove a uniform and a topological variant of the Curtis-Hedlund-Lyndon theorem. In Main Theorem 5, the uniform variant, we show that global transition functions are characterised by  -equivariance and uniform continuity. And in its Corollary 3, the topological variant, that under the assumption that the set of states is finite they are characterised by
-equivariance and uniform continuity. And in its Corollary 3, the topological variant, that under the assumption that the set of states is finite they are characterised by  -equivariance and continuity.
-equivariance and continuity.
Definition 19
Let G be a group equipped with a topology. It is called topological if and only if the maps
are continuous, where \(G \times G\) is equipped with the product topology.
Definition 20
Let M be a set, let \(\mathfrak {L}\) be a subset of the power set of M, and let T be a subset of M. The set T is called transversal of \(\mathfrak {L}\) if and only if there is a surjective map \(f :\mathfrak {L} \rightarrow T\) such that for each set \(A \in \mathfrak {L}\) we have \(f(A) \in A\).
Definition 21
Let M and \(M'\) be two topological spaces and let f be a continuous map from M to \(M'\). The map f is called
-
1.
proper if and only if, for each compact subset K of \(M'\), its preimage \(f^{-1}(K)\) is a compact subset of M;
-
2.
semi-proper if and only if, for each compact subset K of \(M'\), each transversal of \(\{f^{-1}(k) \mid k \in K\}\) is included in a compact subset of M.
Definition 22
Let M be a topological space, let G be a topological group, and let \(\mathcal {M} = ( M, G, \triangleright )\) be a left group set. The group set \(\mathcal {M}\) is called
-
1.
topological if and only if the map \(\triangleright \) is continuous;
-
2.
proper if and only if it is topological and the so-called action map
$$\begin{aligned} \alpha :G \times M&\rightarrow M \times M,\\ (g, m)&\mapsto (g \triangleright m, m), \end{aligned}$$is proper, where \(G \times M\) and \(M \times M\) are equipped with their respective product topology;
-
3.
semi-proper if and only if it is topological and its action map is semi-proper.
Remark 3
Each proper map is semi-proper and each proper left group set is semi-proper.
Lemma 13
Let \(\mathcal {M} = ( M, G, \triangleright )\) be a semi-proper left group set, and let K and \(K'\) be two compact subsets of M. Each transversal of \(\{G_{k', k} \mid (k, k') \in K \times K'\}\) is included in a compact subset of G.
Lemma 14
Let \(\mathcal {M} = ( M, G, \triangleright )\) be a left group set. Equip M and G with their respective discrete topology. The group set \(\mathcal {M}\) is semi-proper.
Definition 23
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a topological or uniform cell space. Equip \(G \slash G_0\) with the topology or uniformity induced by  .
.
Lemma 15
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a semi-proper cell space, let K be a compact subset of M, and let E be a compact subset of \(G \slash G_0\). The set  is included in a compact subset of M.
is included in a compact subset of M.
Definition 24
Let M be a topological space and let Q be a set.
-
1.
The topology on \(Q^M\) that has for a subbase (and base) the sets
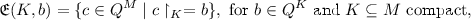
is called topology of discrete convergence on compacta.
-
2.
The uniformity on \(Q^M\) that has for a subbase (and base) the sets

is called uniformity of discrete convergence on compacta.
Remark 4
-
1.
Let M be equipped with the discrete topology. For each subset A of M, the set A is compact if and only if it is finite. Therefore, the topology and uniformity of discrete convergence on compacta on \(Q^M\) are the prodiscrete topology and uniformity on \(Q^M\) respectively. For definitions of the latter see Sects. 1.2 and 1.9 in [1]. The set \(Q^M\) equipped wit the prodiscrete topology is Hausdorff (see Proposition 1.2.1 in [1]) and if Q is finite then it is compact (see the first paragraph in Sect. 1.8 in [1]).
-
2.
If the topological space M is compact, the topology and uniformity of discrete convergence on compacta on \(Q^M\) is the discrete topology and uniformity on \(Q^M\) respectively.
-
3.
The topology induced by the uniformity of discrete convergence on compacta on \(Q^M\) is the topology of discrete convergence on compacta on \(Q^M\).
Remark 5
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space and let Q be a finite set. Equip M and G with their respective discrete topologies, and equip \(Q^M\) with the prodiscrete topology. According to Lemma 14, the cell space \(\mathcal {R}\) is semi-proper. Because the topology on \(G \slash G_0\) is discrete, each subset E of \(G \slash G_0\) is compact if and only if it is finite. Because \(Q^M\) is compact, each map \(\varDelta :Q^M \rightarrow Q^M\) is uniformly continuous if and only if it is continuous. And, because \(Q^M\) is Hausdorff, each map \(\varDelta :Q^M \rightarrow Q^M\), is a uniform isomorphism if and only if it is continuous and bijective.
Main Theorem 5
(Uniform Variant; Morton Landers Curtis, Gustav Arnold Hedlund, and Roger Conant Lyndon, 1969). Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a semi-proper cell space, let Q be a set, let \(\varDelta \) be a map from \(Q^M\) to \(Q^M\), let \(Q^M\) be equipped with the uniformity of discrete convergence on compacta, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). The following statements are equivalent:
-
1.
The map \(\varDelta \) is the global transition function of a semi-cellular automaton with \(\bullet _{H_0}\)-invariant local transition function and compact essential neighbourhood.
-
2.
The map \(\varDelta \) is
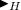 -equivariant and uniformly continuous.
-equivariant and uniformly continuous.
Proof
First, let \(\varDelta \) be the global transition function of a semi-cellular automaton \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) such that \(\delta \) is \(\bullet _{H_0}\)-invariant and such that there is a compact essential neighbourhood E of \(\mathcal {C}\). Then, according to Item 3 of Theorem 2, the map \(\varDelta \) is  -equivariant. Moreover, let K be a compact subset of M. According to Lemma 15, the set
-equivariant. Moreover, let K be a compact subset of M. According to Lemma 15, the set  is included in a compact subset L of M. For each \(c \in Q^M\) and each \(c' \in Q^M\), if
is included in a compact subset L of M. For each \(c \in Q^M\) and each \(c' \in Q^M\), if  , then
, then  , in particular, if
, in particular, if  , then
, then  . Thus,
. Thus,
Because the sets \(\mathfrak {E}(K)\), for \(K \subseteq M\) compact, constitute a base of the uniformity on \(Q^M\), the global transition function \(\varDelta \) is uniformly continuous.
Secondly, let \(\varDelta \) be as in Item 2. Because \(\varDelta \) is uniformly continuous, there is a compact subset \(E_0\) of M such that
Therefore, for each \(c \in Q^M\), the state \(\varDelta (c)(m_0)\) depends at most on  . The subset
. The subset  of \(G \slash G_0\) is compact. Let N be the set \(G_0 \cdot E\). Then, \(G_0 \cdot N \subseteq N\). And, because
of \(G \slash G_0\) is compact. Let N be the set \(G_0 \cdot E\). Then, \(G_0 \cdot N \subseteq N\). And, because  , for each \(c \in Q^M\), the state \(\varDelta (c)(m_0)\) depends at most on
, for each \(c \in Q^M\), the state \(\varDelta (c)(m_0)\) depends at most on  . Hence, there is a map \(\delta :Q^N \rightarrow Q\) such that
. Hence, there is a map \(\delta :Q^N \rightarrow Q\) such that

The quadruple \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) is a semi-cellular automaton. Conclude with Theorem 3 that \(\delta \) is \(\bullet _{H_0}\)-invariant and that \(\varDelta \) is the global transition function of \(\mathcal {C}\). \(\square \)
Corollary 3
(Topological Variant; Morton Landers Curtis, Gustav Arnold Hedlund, and Roger Conant Lyndon, 1969). Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let Q be a finite set, let \(\varDelta \) be a map from \(Q^M\) to \(Q^M\), let \(Q^M\) be equipped with the prodiscrete topology, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). The following statements are equivalent:
-
1.
The map \(\varDelta \) is the global transition function of a semi-cellular automaton with \(\bullet _{H_0}\)-invariant local transition function and finite essential neighbourhood.
-
2.
The map \(\varDelta \) is
 -equivariant and continuous.
-equivariant and continuous.
Proof
With Remark 5 this follows directly from Main Theorem 5. \(\square \)
Remark 6
In the case that \(M = G\) and \(\triangleright \) is the group multiplication of G, Main Theorem 5 is Theorem 1.9.1 in [1] and Corollary 3 is Theorem 1.8.1 in [1].
6 Invertibility
Definition 25
Let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton. It is called invertible if and only if there is a semi-cellular automaton \(\mathcal {C}'\), called inverse to \(\mathcal {C}\), such that the global transition functions of \(\mathcal {C}\) and \(\mathcal {C}'\) are inverse to each other.
Theorem 6
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a semi-proper cell space, let Q be a set, let \(\varDelta \) be a map from \(Q^M\) to \(Q^M\), let \(Q^M\) be equipped with the uniformity of discrete convergence on compacta, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). The following statements are equivalent:
-
1.
The map \(\varDelta \) is the global transition function of an invertible semi-cellular automaton \(\mathcal {C}\) that has an inverse \(\mathcal {C}'\) such that the local transition functions of \(\mathcal {C}\) and \(\mathcal {C}'\) are \(\bullet _{H_0}\)-invariant, and \(\mathcal {C}\) and \(\mathcal {C}'\) have compact essential neighbourhoods.
-
2.
The map \(\varDelta \) is an
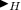 -equivariant uniform isomorphism.
-equivariant uniform isomorphism.
Proof
With Lemma 2 this follows directly from Main Theorem 5.
Corollary 4
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let Q be a finite set, let \(\varDelta \) be a map from \(Q^M\) to \(Q^M\), let \(Q^M\) be equipped with the prodiscrete topology, and let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). The following statements are equivalent:
-
1.
The map \(\varDelta \) is the global transition function of an invertible semi-cellular automaton \(\mathcal {C}\) that has an inverse \(\mathcal {C}'\) such that the local transition functions of \(\mathcal {C}\) and \(\mathcal {C}'\) are \(\bullet _{H_0}\)-invariant, and \(\mathcal {C}\) and \(\mathcal {C}'\) have finite essential neighbourhoods.
-
2.
The map \(\varDelta \) is
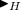 -equivariant, continuous, and bijective.
-equivariant, continuous, and bijective.
Proof
With Remark 5 this follows directly from Theorem 6. \(\square \)
Corollary 5
Let \(\mathcal {R} = ( ( M, G, \triangleright ), ( m_0, \{{g_{m_0, m}}\}_{m \in M}))\) be a cell space, let H be a subgroup of G such that \(\{g_{m_0, m} \mid m \in M\} \subseteq H\). Furthermore, let \(\mathcal {C} = ( \mathcal {R}, Q, N, \delta )\) be a semi-cellular automaton with finite set of states, finite essential neighbourhood, and \(\bullet _{H_0}\)-invariant local transition function. The automaton \(\mathcal {C}\) is invertible if and only if its global transition function is bijective.
Proof
With Item 1 of Theorem 2 and Corollary 3 this follows directly from Corollary 4. \(\square \)
References
Ceccherini-Silberstein, T., Coornaert, M.: Cellular Automata and Groups. Springer Monographs in Mathematics. Springer, Heidelberg (2010)
Hedlund, G.A.: Endomorphisms and automorphisms of the shift dynamical system. Math. Syst. Theory 3(4), 320–375 (1969)
Moriceau, S.: Cellular Automata on a \(G\)-Set. J. Cell. Automata 6(6), 461–486 (2011)
Wacker, S.: Right Amenable Left Group Sets and the Tarski-Følner Theorem. arXiv: 1603.06460 [math.GR]
Wacker, S.: The Garden of Eden Theorem for Cellular Automata on Group Sets. arXiv: 1603.07272 [math.GR]
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Wacker, S. (2016). Cellular Automata on Group Sets and the Uniform Curtis-Hedlund-Lyndon Theorem. In: Cook, M., Neary, T. (eds) Cellular Automata and Discrete Complex Systems. AUTOMATA 2016. Lecture Notes in Computer Science(), vol 9664. Springer, Cham. https://doi.org/10.1007/978-3-319-39300-1_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-39300-1_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-39299-8
Online ISBN: 978-3-319-39300-1
eBook Packages: Computer ScienceComputer Science (R0)


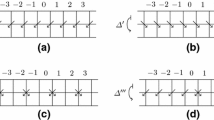


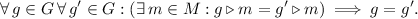

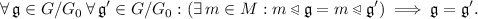
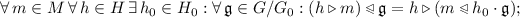

 -equivariant.
-equivariant.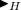 -equivariant map
-equivariant map 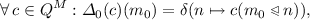
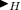 -equivariant.
-equivariant. -equivariant and
-equivariant and 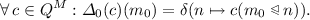
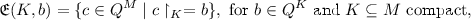

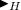 -equivariant and uniformly continuous.
-equivariant and uniformly continuous. -equivariant and continuous.
-equivariant and continuous.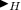 -equivariant uniform isomorphism.
-equivariant uniform isomorphism.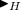 -equivariant, continuous, and bijective.
-equivariant, continuous, and bijective.