Keywords

1 Introduction

In the field of machine learning and bioinformatics the semi-supervised methods present the realization of the technology which uses the data with both known and unknown class labels in order to solve some particular task, such as data clustering or classification. As a rule the number of unlabeled data considerably exceeds the number of the data with known labels. It can be explained by high financial and temporal expenses, connected with the manual data classification in such fields of research as natural language processing, text mining, computational biology etc. In order to make use of a tremendous amount of rapidly coming information, which due to the progress in information technologies can be unlimitedly stored in data bases the special methods of semi-supervised learning are currently of great concern. It is recognized that the unlabeled data together with the sufficiently small amount of constrained ones enable the significant improvement in learning accuracy [1].

The semi-supervised clustering is one of the evolving research directions, used for the data exploratory analysis. The main task of the clustering methods is to reveal the groups of similar data points, according to the specified notion of similarity. There are already several approaches to consider the known constraints between the points in order to guide the clustering process [2, 3]. The semi-supervised learning allows improving the efficiency of the clustering using the available expert knowledge in the form of data labels or the relations between the data points.

For the semi-supervised algorithm, processing the great amount of data, as e.g. biological data it is very important to:

  1. (1)

    automatically determine the number of clusters in the data;

  2. (2)

    take into consideration the available data constraints;

  3. (3)

    automatically select the constraints in more uncertain, transition regions in order to get the high accuracy of results. It must be emphasized that the defined constraints greatly influence the clustering result. The improper constraint selection can even decrease the clustering performance [4]. Recently the most important topic of research is the development of active selection strategies, which search for the most useful constraints [5, 6]. They can minimize the expenses of getting the labeled information without loss of clustering accuracy.

In the paper we propose the approach to semi-supervised fuzzy clustering, based on the active constraint selection algorithm [7]. The semi-supervised fuzzy clustering algorithm [8] takes into account the pairwise constraints and belongs to the class of optimization clustering methods. The basis of such methods is the construction of some optimization function the minimization of which enables to define the optimal cluster parameter values. The experiments on several datasets have shown the improvement of clustering performance with the inclusion of constraints, especially when they were actively selected.

2 Semi-supervised Fuzzy Clustering

In our research we have adopted the fuzzy clustering algorithm, proposed in [8], which is based on the algorithm of competitive agglomeration. The algorithm can automatically determine the number of clusters in the analyzed data and takes into account the data constraints using the extended clustering optimization function. There are two types of constraints: “must link” constraint and “cannot link” constraint for data points. Let \( M \) is the set of “must-link” constraints, i.e. \( \left( {x_{i} ,x_{j} } \right) \in M \) means the data points \( x_{i} \) and \( x_{j} \) lie in the same cluster. The set \( Q \) consists of “cannot-link” constraints, i.e. \( \left( {{\text{x}}_{\text{i}} ,{\text{x}}_{\text{j}} } \right) \in {\text{Q}} \) means the data points \( x_{i} \) and \( x_{j} \) lie in the different clusters. The extended optimization function is the following

$$ \begin{aligned} & J\left( {V,U} \right) = \mathop \sum \limits_{k = 1}^{C} \mathop \sum \limits_{i = 1}^{N} \left( {u_{ik} } \right)^{2} d^{2} \left( {x_{i} ,\mu_{k} } \right) - \alpha (\mathop \sum \limits_{{\left( {x_{i} ,x_{j} } \right) \in M}} \mathop \sum \limits_{k = 1}^{C} \mathop \sum \limits_{l = 1,l \ne k}^{C} u_{ik} u_{jl} \,+ \\ & \mathop \sum \limits_{{\left( {x_{i} ,x_{j} } \right) \in Q}} \mathop \sum \limits_{k = 1}^{C} u_{ik} u_{jk} ) - \beta \mathop \sum \limits_{k = 1}^{C} \mathop \sum \limits_{i = 1}^{N} \left( {u_{ik} } \right)^{2} \quad \\ \end{aligned} $$
(1)

where \( X = \left\{ {x_{i} |i \in \left\{ {1, \ldots ,N} \right\}} \right\} \) is the dataset of size \( N \), \( V = \left\{ {\mu_{k} |k \in \left\{ {1, \ldots ,C} \right\}} \right\} \) is the centers of \( C \) clusters, \( U = \left\{ {u_{ik} |k \in \left\{ {1, \ldots ,C} \right\},i \in \left\{ {1, \ldots ,N} \right\}} \right\} \) is the set of membership degrees. The constraint \( \mathop \sum \limits_{k = 1}^{C} u_{ik} = 1, i = \left\{ {1, \cdots ,N} \right\} \) must be considered.

The cluster centers \( \left( {1 \le k \le C} \right) \) are calculated in iterative fashion as

$$ \mu_{k} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {u_{ik} } \right)^{2} x_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {u_{ik} } \right)^{2} }} $$
(2)

and the cardinalities of the clusters are defined as

$$ N_{s} = \mathop \sum \limits_{i = 1}^{N} u_{is} . $$
(3)

The first component of optimization function (1) presents the FCM optimization term and considers the cluster compactness. The second component consists of two terms: (1) penalty for the violation of the pairwise “must-link” constraints; (2) penalty for the violation of the pairwise “cannot-link” constraints. The weight constant \( \alpha \) determines the relative importance of supervision. The third component in (1) is the sum of squares of cardinalities of the individual clusters and corresponds to the regularization term, which controls the number of clusters. The weight function \( \beta \) of the third component provides the balance between the components and is expressed as

$$ \beta \left( t \right) = \frac{{\eta_{0} exp\left( { - \left| {t - t_{0} } \right|/\tau } \right)}}{{\mathop \sum \nolimits_{j = 1}^{C} \left( {\mathop \sum \nolimits_{i = 1}^{N} u_{ij} } \right)^{2} }} \times \left[ {\mathop \sum \limits_{j = 1}^{C} \mathop \sum \limits_{i = 1}^{N} u_{ij}^{2} d^{2} \left( {x_{j} ,\mu_{j} } \right)} \right] $$
(4)

Function \( \beta \left( t \right) \) allows regulating the data memberships \( u_{ij} \) to clusters and has the small value at the beginning of the optimization process in order to form the initial clusters. After that the weight rises in order to reduce the number of clusters and again falls to diminish its influence on the cluster formation.

We have reconsidered the derivation of the expressions for the modification of the parameters \( u_{rs} = u_{rs}^{FCM} + u_{rs}^{constr} + u_{rs}^{bias} \), \( r = \left\{ {1, \cdots ,N} \right\} \), \( s = \left\{ {1, \cdots ,C} \right\} \) in (1). The expressions are calculated using the Lagrange multipliers and are the following:

$$ \begin{aligned} & u_{rs}^{FCM} = {{\frac{1}{{d^{2} \left( {x_{r} ,\mu_{s} } \right)}}} \mathord{\left/ {\vphantom {{\frac{1}{{d^{2} \left( {x_{r} ,\mu_{s} } \right)}}} {\mathop \sum \nolimits_{k = 1}^{C} \frac{1}{{d^{2} \left( {x_{r} ,\mu_{k} } \right)}}}}} \right. \kern-0pt} {\mathop \sum \nolimits_{k = 1}^{C} \frac{1}{{d^{2} \left( {x_{r} ,\mu_{k} } \right)}}}} \\ & u_{rs}^{constr} = \frac{\alpha }{{2d^{2} \left( {x_{r} ,\mu_{s} } \right)}}\left( {\overline{{C_{{v_{r} }} }} - C_{{v_{rs} }} } \right) \\ & u_{rs}^{bias} = \frac{\beta }{{d^{2} \left( {x_{r} ,\mu_{s} } \right)}}\left( {N_{s} - \overline{{N_{r} }} } \right) \\ \end{aligned} $$
(5)

where \( C_{{v_{rs} }} \) – penalty expression for violation the constraint for the \( rth \) point in the case of \( sth \) cluster, \( \overline{{C_{{v_{r} }} }} \) – weighted average penalty for all clusters for the \( rth \) point, \( \overline{{N_{r} }} \) – weighted average of cluster cardinalities relative to \( rth \) point.

The term \( u_{rs}^{FCM} \) is the same as in FCM; the term \( \text{u}_{{\text{rs}}}^{{\text{constr}}} \) allows decreasing or increasing the membership according to the pairwise constraints, defined by user; the term \( u_{rs}^{bias} \) allows to reduce the cardinalities of the non-informative clusters and to discard them from consideration when the cluster cardinalities are below the threshold.

The important step of the semi-supervised clustering process is the cluster merging, which is executed at each iteration of the optimization procedure. It allows excluding from consideration not only the small clusters, but also the non-informative clusters of different sizes.

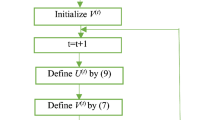
Below is the scheme of the semi-supervised algorithm [8].

3 Active Constraint Selection

In [8] the available constraints, which are selected randomly, significantly increase the performance of data clustering. In our paper we propose to use the active constraint selection algorithm [7], which is able to direct the search for the constraints to the most uncertain (transition) clustering regions. The candidate subset of constraints is constructed on the basis of k-Nearest Neighbor Graph (k-NNG). After that the selection is performed from the list of candidate constraints, sorted according to their ability to separate clusters. As a rule such constraints lie in the most uncertain clustering regions.

The k-NNG graph is constructed using the information about k- nearest neighbors of each data point. The weight \( w(x_{i} ,x_{j} ) \) of the graph edge between two points \( x_{i} \) and \( x_{j} \) is defined as the number of their common nearest neighbors

$$ w(x_{i} ,x_{j} ) = \left| {NN(x_{i} ) \cap NN(x_{j} )} \right|, $$
(6)

where \( NN(x) \) is the k- nearest neighbors of point \( x \).

The constraint ability to separate clusters is estimated using the following utility measure

$$ ASC(x_{i} ,x_{j} ) = \frac{{k - w\left( {x_{i} ,x_{j} } \right) + \frac{1}{{1 + \hbox{min} \left\{ {LDS\left( {x_{i} } \right),\,LDS\left( {x_{j} } \right)} \right\}}}}}{k + 1}, $$
(7)

where \( LDS\left( x \right) = \frac{{\sum\nolimits_{q \in NN(x)} {w(x,q} )}}{k} \) is the local density of point \( x \). The ASC measure of pairwise constraint \( \left( {x_{i} ,x_{j} } \right) \) depends on the corresponding edge weight \( w\left( {x_{i} ,x_{j} } \right) \) and the constraint density, which is defined by minimum of local densities of points \( x_{i} \) and \( x_{j} \). The ASC measure helps to reveal the constraints, which are more informative for clustering, i.e. can improve the clustering performance. The higher ASC value corresponds to more informative constraint.

The candidate constraints are selected using the k-NNG graph as follows

$$ C = \left\{ {\left( {u,v} \right)|w\left( {u,v} \right) < \theta } \right\}, $$
(8)

where \( u,v \) – graph vertices, \( \theta \) – the threshold parameters, defined in the interval \( \left[ {\frac{k}{2} - 2,\frac{k}{2} + 2} \right] \).

In order to refine the constraint selection process the authors in [7] propagate the already selected constraints to the whole set of candidate constraints. The propagation procedure helps to exclude from further consideration the constraints, which can be derived from the already selected ones using the strong path and transitive closure concepts.

According to the algorithm [7] the constraints are defined iteratively, starting from the one constraint till the required number. Each constraint can be selected from the candidate subset C using two variants: (1) random choice of constraints; (2) taking from the constraint list, sorted according to ASC measure. In our research we have compared the active constraint selection procedure, based on ASC measure with purely random choice of constraints from the data.

4 Results of Experiments

Several comparative experiments using fuzzy semi-supervised clustering algorithm with active constraints (AS) and with purely random constraints (RS) were conducted on artificial and real data sets. The results were compared with the simple k-means (KM) and competitive agglomeration algorithm (CA).

The artificial data set Data1 consists of 150 objects with two features. The objects are divided into three clusters, generated according to the multivariate normal distribution and are partly overlapped. The real data set Leukemia consists of two classes – 47 samples of acute lymphoblastic leukemia (ALL) and 25 samples of acute myeloid leukemia (AML) [9]. In order to validate our approach we have taken into account the two subtypes of ALL: 38 samples of B-cell ALL and 9 samples of T-cell T-ALL, analyzing the classification into 3 classes (ground truth). All the samples are characterized by the expression of 7129 genes. After data preprocessing with thresholding and filtering the 3571 genes are selected for further analysis.

The clustering quality was estimated with the external validation criterion using the ground truth. The criterion estimates the similarity of two data partitions. The first partition corresponds to the known class labels. The second partition is calculated on the basis of fuzzy clustering results, where the label for each data point corresponds to the cluster to which it has the highest membership. As the labels of data points in two partitions can be permuted it is necessary to find the correspondence between them, solving the following optimization task:

Let \( \alpha_{1} \) and \( \alpha_{2} \) are two class label functions, defined by two partitions \( \Pi _{k}^{(1)} \), \( \Pi _{k}^{(2)} \) of the set \( X \) into \( k \) groups, i.e. \( \alpha_{i} (x) = j \), if and only if \( x \in \pi_{j}^{(i)} ,\;i = 1,2\;j = 1, \ldots ,k \). For given permutation \( \varphi \) of class labels from set \( V_{k} \) consider the empirical validation criterion:

$$ d_{k} \left( {\alpha_{1} ,\alpha_{2} ,\varphi } \right) = \frac{1}{\left| X \right|}\sum\nolimits_{x \in X} {\alpha_{1} \left( x \right) \ne \varphi \left( {\alpha_{2} \left( x \right)} \right)} , $$
(9)

where \( \delta \) – indicator function \( \alpha_{1} \left( x \right) \ne \varphi \left( {\alpha_{2} \left( x \right)} \right) \):

$$ \delta \left( {\alpha_{1} \left( x \right) \ne \varphi \left( {\alpha_{2} \left( x \right)} \right)} \right) = \left\{ {\begin{array}{*{20}c} {1,\;if\;\alpha_{1} \left( x \right) \ne \varphi \left( {\alpha_{2} \left( x \right)} \right)} \\ {0,\quad otherwise} \\ \end{array} }. \right. $$
(10)

The optimal class label permutation \( \varphi^{*} \) is defined as

$$ \varphi^{*} = \mathop{\arg \min}\nolimits_{\varphi } d_{k} \left({\alpha_{1},\alpha_{2},\varphi} \right) $$
(11)

Figures 1 and 2 present the dependence between the validation criterion and the number of pairwise constraints considered for AS and RS algorithms. The number of constraints is in the range from 0 to 100 in increments of 10. For every number of constraints, 100 experiments were performed with different random selections of the constraints in order to estimate the standard errors for the RS approach. KM and CA algorithms don’t consider the constraints and are depicted for reference. The algorithms CA, RS and AS were initialized with more than real number of clusters and the search for real clustering structure is performed automatically during algorithm execution. According to Figs. 1 and 2 including the random constraints into clustering allows to improve the clustering quality.

Fig. 1.
figure 1

Clustering results for the artificial dataset using cluster validation criterion

Full size image
Fig. 2.
figure 2

Clustering results for Leukemia dataset using cluster validation criterion

Full size image

AS algorithm improves the clustering results even more and requires fewer constraints in order to reach the same clustering quality as the RS algorithm. The cluster centers for the artificial dataset, which are determined by the fuzzy semi-supervised clustering algorithm are shown in Fig. 3.

Fig. 3.
figure 3

Initial and final cluster centers for artificial dataset: a) clustering with 10 random constraints; b) clustering with 10 active constraints.

Full size image

According to Fig. 3 the application of active constraints not only helps to raise the cluster validation measure but also to improve the search for the real number of clusters.

5 Conclusion

The paper presents the approach to semi-supervised fuzzy clustering with active constraints selection. The extended clustering optimization function of the clustering algorithm takes into account the “must link” and “cannot link” constraints on pairwise data positions in the clusters and is based on the scheme, proposed in [8]. We have applied the algorithm of the active constraints selection [7] to generate the constraints for experimental datasets. The clustering results have shown the improved performance with both random and active constraints, included into fuzzy clustering process. The inclusion of active constraints led to better clustering results and to less number of constraints to attain the high level of the clustering quality. Moreover the active constraints help to define the real number of clusters in the competitive agglomeration process. The algorithms’ realization, data modeling and experiments were performed in R Studio environment using the R language [10].