Identity-Based Encryption from Codes with Rank Metric

Abstract

Code-based cryptography has a long history, almost as long as the history of public-key encryption (${\mathsf {PKE}}$). While we can construct almost all primitives from codes such as ${\mathsf {PKE}}$, signature, group signature etc., it is a long standing open problem to construct an identity-based encryption from codes. We solve this problem by relying on codes with rank metric.

The concept of identity-based encryption (${\mathsf {IBE}}$), introduced by Shamir in 1984, allows the use of users’ identifier information such as email as public key for encryption. There are two problems that makes the design of IBE extremely hard: the requirement that the public key can be an arbitrary string and the possibility to extract decryption keys from the public keys. In fact, it took nearly twenty years for the problem of designing an efficient method to implement an ${\mathsf {IBE}}$ to be solved. The known methods of designing ${\mathsf {IBE}}$ are based on different tools: from elliptic curve pairings by Sakai, Ohgishi and Kasahara and by Boneh and Franklin in 2000 and 2001 respectively; from the quadratic residue problem by Cocks in 2001; and finally from the Learning-with-Error problem by Gentry, Peikert, and Vaikuntanathan in 2008.

Among all candidates for post-quantum cryptography, there only exist thus lattice-based ${\mathsf {IBE}}$. In this paper, we propose a new method, based on the hardness of learning problems with rank metric, to design the first code-based ${\mathsf {IBE}}$ scheme. In order to overcome the two above problems in designing an ${\mathsf {IBE}}$ scheme, we first construct a rank-based ${\mathsf {PKE}}$, called ${\mathsf {RankPKE}}$, where the public key space is dense and thus can be obtained from a hash of any identity. We then extract a decryption key from any public key by constructing an trapdoor function which relies on ${\mathsf {RankSign}}$ - a signature scheme from PQCrypto 2014.

In order to prove the security of our schemes, we introduced a new problem for rank metric: the Rank Support Learning problem ($\mathsf {RSL}$). A high technical contribution of the paper is devoted to study in details the hardness of the $\mathsf {RSL}$ problem.

1 Introduction

1.1 Code-Based Cryptography

Code-based cryptography has a long history, which began by the McEliece cryptosystem in 1978, followed by the Niederreiter scheme in 1986 [39]. The difficult problem involved in these cryptosystems is the Syndrome Decoding problem, which consists in recovering from a random matrix ${\varvec{H}}$ and from a syndrome ${\varvec{s}}={\varvec{H}}{\varvec{e}}^T$, the small (Hamming) weight error vector ${\varvec{e}}$ associated to ${\varvec{s}}$. The idea of these encryption schemes is to consider as public key a masking of a decodable code. Although this masking could be broken for some special families of codes like Reed-Solomon codes or Reed-Muller codes, the original family of binary Goppa codes proposed by McEliece in 1978 is still today considered as secure, and the indistinguishability of Goppa codes from random codes for standard encryption parameters remains unbroken. Few years later Alekhnovich proposed in 2003 [2] a cryptosystem relying on random instances of codes but with larger size of encrypted messages. Code-based cryptosystems had still very large public keys, but from the year 2005 [23], inspired by the NTRU approach, structured matrices, and in particular quasi-cyclic matrices, where also considered for public keys leading to cryptosystems with only a small hidden structure like for instance the MDPC cryptosystem of 2013 [38].

However, when signature schemes were already known for a long time in number theory based cryptography, finding a signature scheme (not based on the Fiat-Shamir heuristic) had been an open problem for quite some time, until the CFS scheme of Courtois, Finiasz and Sendrier in 2001 [16], the scheme is an hash-and-sign signature which computes a signature as a small (Hamming) weight vector associated to a random syndrome. Although this latter scheme has some advantages, like a short signature size, the small weight vector has a logarithmic weight in the length of the code, which implies a super polynomial complexity and very large public keys, which makes it difficult to use it for advanced encryption schemes like for instance identity-based encryption.

Beside systems based on the Hamming metric, cryptosystems relying on a different metric, the rank metric, were introduced in 1991 by Gabidulin et al. [22]. This system, which is an analogue of the McEliece cryptosystem but with a different metric was based on Gabidulin codes, which are analogue codes to Reed-Solomon codes for rank metric. These codes having a very strong structure, they were difficult to mask (as their Hamming counterpart the Reed-Solomon codes), and in practice all cryptosystems based on these codes were broken. Meanwhile the rank metric approach had a strong advantage over the Hamming approach, the fact that the generic decoding problems are inherently more difficult than for Hamming metric. In some sense the general decoding problems for rank metric are to Hamming metric, what is the discrete logarithm problem over the group of an elliptic curve rather than on the ring $\mathbb {Z}/p\mathbb {Z}$. Again, following the approach of NTRU and the (Hamming) MDPC cryptosystem, an analogue cryptosystem, was proposed in 2013 for rank metric: the Low Rank Parity Check (LRPC) cryptosystem [25], as its cousins the MDPC and the NTRU cryptosystems, this system benefits from a poor structure which also seems (as for MDPC and NTRU) to limit the attacks to general attacks on the rank syndrome decoding problem.

In 2014, a new signature scheme, the RankSign scheme, based on LRPC codes was introduced by Gaborit et al. at PQCrypto 2014, [28]. This signature scheme is also a hash-and-sign signature scheme which inverts a random syndrome, but at the difference of the CFS scheme, the weight of the returned signature is linear in the length of the code, which implies smaller size of public key. Moreover beside its poor structure, inherited from the LRPC structure, the system comes with a security proof on information leaking from signatures. Thus we are eventually able to use this hash-and-sign signature scheme as a brick for the first IBE scheme based on coding theory.

1.2 Identity Based Encryption

The notion of identity-based encryption (IBE) was introduced by Shamir [43]. This gives an alternative to the standard notion of public-key encryption. In an IBE scheme, the public key associated with a user can be an arbitrary identity string, such as his e-mail address, and others can send encrypted messages to a user using this arbitrary identity without having to rely on a public-key infrastructure.

The main technical difference between a public key encryption (PKE) and IBE is the way the public and private keys are bound and the way of verifying those keys. In a PKE scheme, verification is achieved through the use of a certificate which relies on a public-key infrastructure. In an IBE, there is no need of verification of the public key but the private key is managed by a Trusted Authority (TA).

Difficulty in designing an IBE. There are two main difficulties in designing an IBE in comparison with a PKE

• 1. In a PKE, one often generates a public key from a secret key and normally, well-formed public keys are exponentially sparse. In an IBE scheme, any identity should be mapped to a public key and there is no known technique to randomly generate a point in an exponentially sparse space. Regev’s public key encryption is an example [41]. In order to circumvent this problem, Gentry et. al. proposed a “dual” of a public-key cryptosystem, in which public keys are first generated in a primal space such that they are dense: every point in the primal space corresponds to a public-key and thus via a random oracle, one can map any identity to a valid public key.

• 2. For some PKE, the public keys are dense and one can thus map any identity to a well-formed public key. However, the difficulty is to extract the corresponding secret key from the public key. ElGamal’s public key encryption [18] is an example because from a public key y in a cyclic group generated by g, there is no trapdoor for the discrete log problem that allows to find the corresponding secret key x such that $g^x=y$. In order to circumvent this problem, bilinear maps have been used [10].

Beside the technical difficulties in the design, achieving security in IBE is much more complicated than in PKE. The main difference is that in IBE, except the challenge identity that the adversary aims to attack, any other identities can be corrupted. Therefore the simulator has to be able to generate secret keys for all identities but the challenge identity. Under the above difficulties in the design and in proving the security, it took nearly twenty years for finding efficient methods to implement IBE.

There are currently three classes of IBE schemes: from elliptic curve pairings introduced by Sakai, Ohgishi and Kasahara [42] and by Boneh and Franklin in [10]; from the quadratic residue problem by Cocks in 2001 [15]; and from hard problems on lattice by Gentry, Peikert, and Vaikuntanathan [31]. These pioneer works inspired then many other ideas to improve the efficiency or to strengthen the security, in particular to avoid the use of the random oracle. We can name some very interesting schemes in the standard model: pairing-based schemes [8, 9, 12, 30, 46, 47] and lattice-based scheme [1, 11, 13]. It is still not known how to devise an IBE scheme from quadratic residue problem without random oracles. We explain below a new method to achieve the first IBE scheme in the coding theory, with the help of rank metric codes and in the random oracle model.

Achieving IBE in Euclidean Metric. Let us first recall the technique in lattice that helps to construct IBE schemes. One of the major breakthroughs in lattice cryptography was the work of Gentry, Peikert, and Vaikuntanathan [31], that showed how to use a short trapdoor basis to generate short lattice vectors without revealing the trapdoor. This was used to give the first lattice-based construction of a secure identity-based encryption scheme.

Let us start with Regev’s scheme [41]. Associated to a matrix ${\varvec{A}}\in \mathbb {Z}_q^{n\times m}$, one generates the public key as ${\varvec{p}}= {\varvec{s}}A+{\varvec{e}}$ for ${\varvec{s}}\in \mathbb {Z}_q^n$ and a short vector ${\varvec{e}}$. The set of possible public keys are points near a lattice point and are thus exponentially sparse. Gentry, Peikert, and Vaikuntanathan introduced a dual version of the Regev’s scheme in exchanging the role of public key and of secret key in defining the public key as ${\varvec{u}}\mathop {=}\limits ^{\text {def}}A{\varvec{e}}^T \mod q$ for short ${\varvec{e}}\in \mathbb {Z}^m$. The public keys are now dense, any identity could be mapped via a random oracle to a point in $\mathbb {Z}_q^{n}$ which will then be used as the corresponding public key. The key property is, with a carefully designed trapdoor ${\varvec{T}}$, from a random public key ${\varvec{u}}\in \mathbb {Z}_q^n$, the preimage ${\varvec{e}}$ of the function $f_{{\varvec{A}}}({\varvec{e}}):= A{\varvec{e}}\mod q$ can be sampled in a space of well-defined short vectors used as the secret keys.

Achieving IBE in Rank Metric: Our technique. It seems very hard to give a rank metric analogue version of the above lattice technique. The main reason is due to the difficulty of obtaining a robust analysis of such a presampling function. However, we can overcome this difficulty in another way which perfectly fits the rank metric. We still keep the public key as ${\varvec{p}}= {\varvec{s}}A+{\varvec{e}}$ for ${\varvec{e}}$ of low rank (say at most r) in $\mathbb {F}_{q^m}^{n}$, and for ${\varvec{A}}$ and ${\varvec{s}}$ drawn uniformly at random in $\mathbb {F}_{q^m}^{(n-k)\times n}$ and $\mathbb {F}_{q^m}^{n-k}$ respectively, where $\mathbb {F}_{q^m}$ is the finite field over $q^m$ elements. The main feature of the rank metric which will be used in what follows is that we can choose the bound r to be above the Gilbert Varshamov (RGV) bound for rank codes and this gives us two ingredients to design an IBE:

• with r carefully chosen above the RGV bound, we can still invert the function $f({\varvec{s}},{\varvec{e}})= {\varvec{s}}A+{\varvec{e}}$. This relies on the RankSign system with a trapdoor to compute the pre-image of the function f [28].

• with overwhelming probability, any point ${\varvec{p}}$ has a preimage $({\varvec{s}},{\varvec{e}})$ such that $f({\varvec{s}},{\varvec{e}})={\varvec{p}}$. We can thus map an arbitrary identity to a valid public key ${\varvec{p}}$, by using a random oracle as in the case of the GPV scheme.

Rank Metric vs. Hamming and Euclidean Metric. Rank metric and Hamming metric are very different metrics. This difference reflects for instance in the size of balls: when the number of elements of a ball of radius r in the Hamming metric for $\{0,1\}^n$ is bounded above by $2^n$, for rank metric the number of elements is exponential but with a quadratic exponent depending on r. In practice, it means that even if it is possible to construct a trapdoor function for the Hamming distance such as the CFS signature scheme [16], the dimension of the dual code used there has to be sublinear in its length, whereas for rank metric it is possible to obtain such a trapdoor function for constant rate codes. This latter property makes it very difficult to use such a trapdoor function for the Hamming distance in order to build an IBE scheme whereas it is tractable for the rank metric.

Moreover one strong advantage of rank metric is the potential size of public keys. If one considers the general syndrome decoding problem ${\varvec{H}}{\varvec{x}}^T={\varvec{s}}$ (for the hardest case), because of the complexity of the best known attacks for rank metric (see [27]), and for $\lambda$ a security parameter, the size of ${\varvec{H}}$ is in $\mathcal {O}\big (\lambda ^{\frac{3}{2}}\big )$ for rank metric when it is in $\mathcal {O}\big ({\lambda ^2}\big )$ for Hamming and Euclidean metrics.

1.3 Hardness of Problems in Rank Metric

The computational complexity of decoding $\mathbb {F}_{q^m}$-linear codes for rank metric has been an open question for almost 25 years since the first paper on rank based cryptography in 1991 [22]. Recently a probabilistic reduction to decoding in Hamming distance was given in [29]. On a practical complexity point of view the complexity of practical attacks grows very fast with the size of parameters, and there is a structural reason for this: for Hamming distance a key notion in the attacks is counting the number of words of length n and support size t, which corresponds to the notion of Newton binomial coefficient $\left( {\begin{array}{c}n\\ t\end{array}}\right)$, whose value is exponential and upper bounded by $2^n$. In the case of rank metric, counting the number of possible supports of size r for a rank code of length n over $\mathbb {F}_{q^m}$ corresponds to counting the number of subspaces of dimension r in $\mathbb {F}_{q^m}$: the Gaussian binomial coefficient of size roughly $q^{r(m-r)}$, whose value is also exponential but with a quadratic term in the exponent.

1.4 Our Contribution

The contributions of this paper are two-fold:

• On the cryptographic aspect: we design new cryptographic primitives based on the rank metric. The final objective is to design an IBE scheme, but on the way, we also introduce a new PKE scheme which perfectly fits a transformation from PKE to IBE. This shows a potential versatility of the use of rank metric in cryptography: it gives a credible alternative to Euclidean metric in the perspective of post-quantum cryptography and it has some advantages compared to Hamming metric as it is still a open question to construct an IBE scheme based on the Hamming metric. We emphasize that the design of an IBE scheme often opens the way to reach more advanced primitives such as Broadcast Encryption, Attribute-based Encryption and Functional Encryption.

• On the algorithmic aspect: the security of the new constructions that we introduce relies on the hardness of three algorithmic problems. Two of them are well known problems, namely the Rank Syndrome Decoding Problem and the Augmented Low Rank Parity Check Code problem. However the last one is new and we call it the Rank Support Learning problem. A large part of the paper is devoted to study the hardness of the Rank Support Learning problem and more specifically

• we prove the equivalence between the Rank Support Learning problem and Rank Decoding with parity-check matrices defined over a subfield;

• we show that this problem can also be tackled by finding low weight-codewords in a certain code;

• we show that this problem can be viewed as the rank metric analogue of a rather old problem in the Hamming metric for which the best known algorithms are exponential;

• based on this analogy we give an algorithm of exponential complexity to handle this problem over the rank metric.

2 Background on Rank Metric and Cryptography

2.1 Notation

In the whole article, q denotes a power of a prime p. The finite field with q elements is denoted by $\mathbb {F}_q$ and more generally for any positive integer m the finite field with $q^m$ elements is denoted by $\mathbb {F}_{q^m}$. We will frequently view $\mathbb {F}_{q^m}$ as an m-dimensional vector space over $\mathbb {F}_q$.

We use bold lowercase and capital letters to denote vectors and matrices respectively. We will view vectors here either as column or row vectors. It will be clear from the context whether it is a column or a row vector. For two matrices ${\varvec{A}}, {\varvec{B}}$ of compatible dimensions, we let $({\varvec{A}}|{\varvec{B}})$ and $\begin{pmatrix} {\varvec{A}}\\ \hline {\varvec{B}}\end{pmatrix}$ respectively denote the horizontal and vertical concatenations of ${\varvec{A}}$ and ${\varvec{B}}$.

If S is a finite set, $x \mathop {\leftarrow }\limits ^{\$}S$ denotes that x is chosen uniformly at random among S. If $\mathcal {D}$ is a distribution, $x \leftarrow \mathcal {D}$ denotes that x is chosen at random according to $\mathcal {D}$.

We also use the standard $\mathcal {O}\big ( \big )$, $\varOmega ()$ and $\varTheta ()$ notation and also the “soft-O” notation , where means that $f(x) = \mathcal {O}\big ({g(x) \log (g(x))^k}\big )$ for some k.

2.2 Definitions

In the whole article, the space $\mathbb {F}_{q^m}^n$ will be endowed with the following metric

Definition 1

(Rank metric over $\mathbb {F}_{q^m}^n$ ). Let ${\varvec{x}}=(x_1,\dots ,x_n) \in \mathbb {F}_{q^m}^n$ and consider an arbitrary basis $(\beta _1,\dots ,\beta _m) \in \mathbb {F}_{q^m}^m$ of $\mathbb {F}_{q^m}$ viewed as an m-dimensional vector space over $\mathbb {F}_q$. We decompose each entry $x_j$ in this basis $x_j = \sum _{i=1}^m m_{ij} \beta _i$. The $m \times n$ matrix associated to ${\varvec{x}}$ is given by ${\varvec{M}}({\varvec{x}})=(m_{ij})_{\begin{array}{c} 1 \le i \le m \\ 1 \le j \le n \end{array}}$. The rank weight $\Vert {\varvec{x}} \Vert$ of ${\varvec{x}}$ is defined as

$$ \Vert {\varvec{x}} \Vert \mathop {=}\limits ^{\text {def}}{{\mathrm{Rank}}}{\varvec{M}}({\varvec{x}}). $$

The associated distance $\mathrm{rd}({\varvec{x}},{\varvec{y}})$ between elements ${\varvec{x}}$ and ${\varvec{y}}$ in $\mathbb {F}_{q^m}^n$ is defined by $\mathrm{rd}({\varvec{x}},{\varvec{y}})=\Vert {\varvec{x}}-{\varvec{y}} \Vert$.

Remark 1

It is readily seen that this distance does not depend on the basis that is chosen. We refer to [37] for more details on the rank distance.

A rank code ${\mathcal {C}}$ of length n and dimension k over the field $\mathbb {F}_{q^m}$ is a subspace of dimension k of $\mathbb {F}_{q^m}^n$ embedded with the rank metric. The minimum rank distance of the code ${\mathcal {C}}$ is the minimum rank of non-zero vectors of the code. One also considers the usual inner product which allows to define the notion of dual code. An important notion which differs from the Hamming distance, is the notion of support. Let ${\varvec{x}}=(x_1,x_2,\cdots ,x_n) \in \mathbb {F}_{q^m}^n$ be a vector of rank weight r. We denote by $E \mathop {=}\limits ^{\text {def}}\langle x_1,x_2,\cdots ,x_n\rangle _{\mathbb {F}_q}$ the $\mathbb {F}_q$-linear subspace of $\mathbb {F}_{q^m}$ generated by linear combinations over $\mathbb {F}_q$ of $x_1,x_2,\cdots ,x_n$. The vector space E is called the support of ${\varvec{x}}$ and is denoted by ${{\mathrm{Supp}}}({\varvec{x}})$. In the following, ${\mathcal {C}}$ is a rank metric code of length n and dimension k over $\mathbb {F}_{q^m}$. The matrix ${\varvec{G}}$ denotes a $k \times n$ generator matrix of ${\mathcal {C}}$ and ${\varvec{H}}$ is one of its parity check matrix.

Bounds for Rank Metric Codes. The classical bounds for the Hamming metric have straightforward rank metric analogues, since two of them are of interest for the paper we recall them below.

Definition 2

(Rank Gilbert-Varshamov bound (RGV)). The number of elements S(n, m, q, t) of a sphere of radius t in $\mathbb {F}_{q^m}^n$, is equal to the number of $m \times n$ q-ary matrices of rank t. For $t=0$ $S_0=1$, for $t \ge 1$ we have (see [37]):

$$\begin{aligned} S(n,m,q,t)= \prod _{j=0}^{t-1} \frac{(q^n-q^j)(q^m-q^j)}{q^t-q^j}. \end{aligned}$$

From this we deduce the volume B(n, m, q, t) of a ball of radius t in $\mathbb {F}_{q^m}^n$ to be:

$$\begin{aligned} B(n,m,q,t)= \sum _{i=0}^tS(n,m,q,i). \end{aligned}$$

In the linear case the Rank Gilbert-Varshamov bound RGV(n, k, m, q) for an [n, k] linear code over $\mathbb {F}_{q^m}$ is then defined as the smallest integer t such that $B(n,m,q,t) \ge q^{m(n-k)}$.

The Gilbert-Varshamov bound for a rank code ${\mathcal {C}}$ with parity-check matrix ${\varvec{H}}$, corresponds to the smallest rank weight r for which, for any syndrome ${\varvec{s}}$, there exists on average a word ${\varvec{e}}$ of rank weight r such that ${\varvec{H}}{\varvec{e}}={\varvec{s}}$. To give an idea of the behavior of this bound, it can be shown that, asymptotically in the case $m=n$ [37]: $\frac{RGV(n,k,m,q)}{n} \sim 1-\sqrt{\frac{k}{n}}$.

Singleton Bound. The classical Singleton bound for a linear [n, k] rank code of minimum rank r over $\mathbb {F}_{q^m}$ works in the same way as for linear codes (by finding an information set) and reads $r \le n-k+1$: in the case when $n > m$ this bound can be rewritten as $r \le 1+ \lfloor \frac{(n-k)m}{n} \rfloor$ [37].

2.3 Decoding Rank Codes

We will be interested in codes for the rank metric which can be efficiently decoded. At the difference of Hamming metric, there do not exist many families which admit an efficient decoding for large rank weight error (ideally we would like to go up to the RGV bound).

Deterministic Decoding of Rank Codes. Essentially there is only one family of rank codes which can be decoded in a deterministic way: the Gabidulin codes [21]. These codes are an analogue of the Reed-Solomon codes where polynomials are replaced by q-polynomials and benefit from the same decoding properties (cf [21] for more properties on these codes). A Gabidulin code of length n and dimension k over $\mathbb {F}_{q^m}$ with $k \le n \le m$ can decode up to $\frac{n-k}{2}$ errors in a deterministic way.

Probabilistic Decoding of Rank Codes. Besides the deterministic decoding of Gabidulin codes, which does not reach the RGV bound and hence is not optimal, it is possible to decode up to the RGV bound a simple family of codes. In this subsection we present the construction which allows with a probabilistic decoding algorithm to attain the RGV bound. These codes are adapted from codes in the subspace metric (a metric very close from the rank metric) which can be found in [44].

Definition 3

(Simple codes). A code ${\mathcal {C}}$ is said to be (n, k, t)-simple (or just simple when t, k n are clear from the context), when it has a parity-check matrix ${\varvec{H}}$ of the form

$$ {\varvec{H}}= \left( \begin{array}{ccc} \\ &{}{\varvec{I}}_{n-k}&{}\\ \\ \end{array}\right| \left. \begin{array}{c} \varvec{0_t} \\ \hline \\ {\varvec{R}}\end{array}\right) $$

where ${\varvec{I}}_{n-k}$ the $(n-k) \times (n-k)$ identity matrix, $\varvec{0_t}$ is the zero matrix of size $t\times k$ and ${\varvec{R}}$ is a matrix over $\mathbb {F}_{q^m}$ of size $k \times (n-k-t)$. It is called a random simple code if ${\varvec{R}}$ is chosen uniformly at random among matrices of this size.

Proposition 1

Let ${\mathcal {C}}$ be a random (n, k, t)-simple code with $t < \frac{m+n-\sqrt{(m-n)^2+4\,\mathrm{km}}}{2}$ and w an integer. If $w \leqslant t$ then ${\mathcal {C}}$ can decode an error of weight w with probability of failure $p_f \sim \frac{1}{q^{t-w+1}}$ when $q\rightarrow \infty$.

The proof of this proposition is given in the full version of this paper [26]. The success of decoding depends essentially on the probability $1-p_f$ to recover the space E from the t first coordinates of ${\varvec{s}}$, this probability can be made as small as needed by decoding less than t errors or by increasing q.

In term of complexity of decoding, one has just a system to invert in $(n-t)w$ unknowns in $\mathbb {F}_q$. Notice that the bound $\frac{m+n-\sqrt{(m-n)^2+4\,\mathrm{km}}}{2}$ corresponds asymptotically to the Rank Gilbert-Varshamov bound. Thus a simple code can asymptotically decodes up to the Rank Gilbert-Varshamov bound with probability $1-\mathcal {O}\big ({\frac{1}{q}}\big )$.

In the special case $m=n$ and $w=t \approx n\left( 1-\sqrt{\frac{k}{n}} \right)$ (the Rank Gilbert-Varshamov bound), the system has $\mathcal {O}\big ({n^2}\big )$ unknowns, so the decoding complexity is bounded by $\mathcal {O}\big ({n^6}\big )$ operations in $\mathbb {F}_q$. This decoding algorithm is better than the Gabidulin code decoder in term of correction capability since it corrects up to $n\left( 1-\sqrt{\frac{k}{n}} \right)$ errors when Gabidulin codes can not decode more than $\frac{n-k}{2}$ errors.

2.4 Difficult Problem for Rank-Based Cryptography

Rank-based cryptography generally relies on the hardness of syndrome decoding for the rank metric. It is defined as the well known syndrome decoding problem but here the Hamming metric is replaced by the rank metric.

Definition 4

(Rank (Metric) Syndrome Decoding Problem ($\mathsf {RSD}$)). Let ${\varvec{H}}$ be a full-rank $(n-k)\times n$ matrix over $\mathbb {F}_{q^m}$ with $k \le n$, ${\varvec{s}}\in \mathbb {F}_{q^m}^{n-k}$ and w an integer. The problem is to find ${\varvec{x}}\in \mathbb {F}_{q^m}^n$ such that $\mathrm{rank}({\varvec{x}})=w$ and ${\varvec{H}}{\varvec{x}}={\varvec{s}}$. We denote this problem as the $\mathsf {RSD}_{q,m,n,k,w}$ problem.

The $\mathsf {RSD}$ problem has recently been proven hard in [29] on probabilistic reduction. This problem has an equivalent dual version. Let ${\varvec{H}}$ be a parity-check matrix of a code ${\mathcal {C}}$ and ${\varvec{G}}$ be a generator matrix. Then the $\mathsf {RSD}$ problem is equivalent to find ${\varvec{m}}\in \mathbb {F}_{q^m}^k$ and ${\varvec{x}}\in \mathbb {F}_{q^m}^n$ such that ${\varvec{m}}{\varvec{G}}+{\varvec{x}}={\varvec{y}}$ with ${{\mathrm{Rank}}}{{\varvec{x}}} = r$ and ${\varvec{y}}$ some preimage of ${\varvec{s}}$ by ${\varvec{H}}$. We can now give the decisional version of this problem:

Definition 5

(Decisional Rank Syndrome Decoding Problem ($\mathsf {DRSD}$)). Let ${\varvec{G}}$ be a full-rank $k\times n$ matrix over $\mathbb {F}_{q^m}$, ${\varvec{m}}\in \mathbb {F}_{q^m}^k$ and ${\varvec{x}}\in \mathbb {F}_{q^m}^n$ of weight r. Can we distinguish the pair $({\varvec{G}},{\varvec{m}}{\varvec{G}}+{\varvec{x}})$ from $({\varvec{G}},{\varvec{y}})$ with ${\varvec{y}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^n$?

The same problem in the Hamming metric Decisional Syndrome Decoding problem ($\mathsf {DSD}$), viewed as an LPN problem with a fixed number of samples (which is equivalent to the syndrome decoding problem), is proven hard in [3] with a reduction to the syndrome decoding problem for the Hamming metric. We can use the same technique as in [24, 29] to prove that $\mathsf {DRSD}$ is hard in the worst case. The general idea is that a distinguisher $D_R$ with non negligible advantage for $\mathsf {DRSD}$ problem can be used to construct another distinguisher D for $\mathsf {DSD}$ with a non negligible advantage.

2.5 Complexity of the Rank Decoding Problem

As explained earlier in the introduction the complexity of practical attacks grows very fast with the size of parameters, there exist two types of generic attacks on the problem:

• Combinatorial attacks: these attacks are usually the best ones for small values of q (typically $q=2$) and when n and k are not too small; when q increases, the combinatorial aspect makes them less efficient. The best attacks generalize the basic information set decoding approach in a rank metric context. Interestingly enough, the more recent improvements based on birthday paradox do not seem to generalize in rank metric because of the different notion of support.

  In practice, when $m \leqslant n$, the best combinatorial attacks have complexity $\mathcal {O}\big ({(n-k)^3m^3q^{(r-1)\lfloor \frac{(k+1)m}{n}\rfloor }}\big )$ [27].

• Algebraic attacks: the particular nature of rank metric makes it a natural field for algebraic attacks and solving by Groebner basis, since these attacks are largely independent of the value of q and in some cases may also be largely independent on m. These attacks are usually the most efficient ones when q increases. There exist different types of algebraic modeling which can then be solved with Groebner basis techniques [19, 20, 27, 36]. Algebraic attacks usually consider algebraic systems on the base field $\mathbb {F}_q$, it implies that the number of unknowns is quadratic in the length of the code. Since the general complexity of Groebner basis attacks is exponential in the number of unknowns, it induces for cryptographic parameters, general attacks with a quadratic exponent in the length of the code, as for combinatorial attacks.

3 A New Public Key Encryption

3.1 Public-Key Encryption

Let us briefly remind that a public-key encryption scheme $\mathcal S$ is defined by three algorithms: the key generation algorithm ${\mathsf {KeyGen}}$ which, on input the security parameter, produces a pair of matching public and private keys $( pk , sk )$; the encryption algorithm ${\mathsf {Enc}}_ pk (m;r)$ which outputs a ciphertext c corresponding to the plaintext $m\in \mathcal {M}$, using random coins $r\in \mathcal {R}$; and the decryption algorithm ${\mathsf {Dec}}_ sk (c)$ which outputs the plaintext m associated to the ciphertext c.

It is now well-admitted to require semantic security (a.k.a. polynomial security or indistinguishability of encryptions [32], denoted $\mathsf {IND}$): if the attacker has some a priori information about the plaintext, it should not learn more with the view of the ciphertext. More formally, this security notion requires the computational indistinguishability between two messages, chosen by the adversary, one of which has been encrypted. The issue is to find which one has been actually encrypted with a probability significantly better than one half. More precisely, we define the advantage $\mathsf {Adv}^{\mathsf {ind}}_{\mathcal S}(\mathcal {A})$, where the adversary $\mathcal {A}$ is seen as a 2-stage Turing machine $(\mathcal {A}_1,\mathcal {A}_2)$ by

$$ \mathsf {Adv}^{\mathsf {ind}}_{\mathcal S}(\mathcal {A}) \mathop {=}\limits ^{\text {def}}2 \times \Pr \left[ \begin{array}{l} ( pk , sk )\leftarrow {\mathsf {KeyGen}}, (m_0,m_1,s)\leftarrow \mathcal {A}_1( pk ), \\ b\mathop {\leftarrow }\limits ^{R}\{0,1\}, c={\mathsf {Enc}}_{ pk }(m_b): \mathcal {A}_2(m_0,m_1,s,c) = b \end{array} \right] - 1.$$

This advantage should ideally be a negligible function of the security parameter.

3.2 Description of the Cryptosystem ${\mathsf {RankPKE}}$

First, we need to define what we call a homogeneous matrix which will be used in encryption.

Definition 6

(Homogeneous Matrix). A matrix ${\varvec{M}}=(m_{ij})_{\begin{array}{c} 1 \le i \le a \\ 1 \le j \le b \end{array}} \in \mathbb {F}_{q^m}^{a \times b}$ is homogeneous of weight d if all its coefficients belong to the same $\mathbb {F}_q$-vector subspace of dimension d, that is to say

$$\begin{aligned} \dim _{\mathbb {F}_q} \langle m_{ij} \rangle = d \end{aligned}$$

We now introduce a public-key encryption, called ${\mathsf {RankPKE}}$. Let ${\varvec{A}}$ be drawn uniformly at random in $\mathbb {F}_{q^m}^{(n-k)\times n}$. We need it to be of full rank. This happens with overwhelming probability (i.e. $1 - \mathcal {O}\big ({q^{-m(k+1)}}\big )$). Let $W_r$ be the set of all the words of rank r and of length n, i.e. $W_r = \{{\varvec{x}}\in \mathbb {F}_{q^m}^n : \Vert {\varvec{x}} \Vert = r \}$. The system ${\mathsf {RankPKE}}$ works as follows:

• ${\mathsf {RankPKE}}.{\mathsf {KeyGen}}$:

  • generate ${\varvec{A}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{(n-k)\times n}$

  • generate ${\varvec{s}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n-k}$ and ${\varvec{e}}\mathop {\leftarrow }\limits ^{\$}W_r$

  • compute ${\varvec{p}}= {\varvec{s}}{\varvec{A}}+{\varvec{e}}$

  • define ${\varvec{G}}\in \mathbb {F}_{q^m}^{k'\times n'}$ a generator matrix of a public code ${\mathcal {C}}$ which can decode (efficiently) errors of weight up to wr, where w is defined just below.

  • define $sk = {\varvec{s}}$ and $pk =({\varvec{A}},{\varvec{p}},{\varvec{G}})$

• ${\mathsf {RankPKE}}.{\mathsf {Enc}}(({\varvec{A}},{\varvec{p}},{\varvec{G}}),{\varvec{m}})$: Let ${\varvec{m}}\in \mathbb {F}_{q^m}^{k'}$ be the message we want to encrypt. We generate a random homogeneous matrix ${\varvec{U}}\in \mathbb {F}_{q^m}^{n\times n'}$ of weight w. Then we can compute the ciphertext $({\varvec{C}},{\varvec{x}})$ of ${\varvec{m}}$ as :

  

• ${\mathsf {RankPKE}}.{\mathsf {Dec}}({\varvec{s}},({\varvec{C}},{\varvec{x}}))$:

  • use the secret key ${\varvec{s}}$ to compute:

    

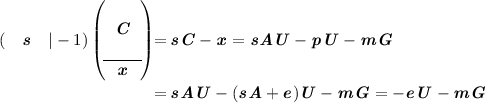
  • since ${\varvec{U}}$ is homogeneous, we have $\Vert {\varvec{e}}{\varvec{U}} \Vert \leqslant wr$. Therefore, by using the decoding algorithm of ${\mathcal {C}}$, we recover ${\varvec{m}}$.

The expansion rate of this cryptosystem is $\frac{n-k+1}{R}$ where $R = \frac{k'}{n'}$ is the rate of ${\mathcal {C}}$.

3.3 Security

Definition 7

(Rank Support Learning ($\mathsf {RSL}$)). Let ${\varvec{A}}$ be a random full-rank matrix of size $(n-k)\times n$ over $\mathbb {F}_{q^m}$ and V be a subspace of $\mathbb {F}_{q^m}$ of dimension w. Let $\mathcal {O}$ be an oracle which gives samples of the form $({\varvec{A}},{\varvec{A}}{\varvec{u}})$, where ${\varvec{u}}\mathop {\leftarrow }\limits ^{\$}V^n$. The $\mathsf {RSL}_{q,m,n,k,w}$ problem is to recover V given only access to the oracle.

We say that the problem is $(N,t,\varepsilon )$-hard if for every probabilistic algorithm $\mathcal {A}$ running in time t, we have

$$\begin{aligned} {{\mathrm{Prob}}}[\mathcal {A}({\varvec{A}},{\varvec{A}}{\varvec{U}}) = V] \leqslant \varepsilon ,\quad {\varvec{U}}\mathop {\leftarrow }\limits ^{\$}V^{n\times N} \end{aligned}$$

When we want to stress the fact that we care about the problem where we are allowed to make exactly N calls to the oracle, we denote this the $\mathsf {RSL}_{q,m,n,k,w,N}$ problem. The pair $({\varvec{A}},{\varvec{A}}{\varvec{U}})$ is referred to as an instance of the $\mathsf {RSL}_{q,m,n,k,w,N}$ problem.

The corresponding decisional problem, namely $\mathsf {DRSL}$, is to distinguish $({\varvec{A}},{\varvec{A}}{\varvec{U}})$ from $({\varvec{A}},{\varvec{Y}})$ where ${\varvec{Y}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{(n-k)\times N}$.

Proposition 2

The $\mathsf {RSL}_{q,m,n,k,w,N}$ is as hard as the $\mathsf {RSD}_{q,m,n,k,w}$ problem.

Proof

Let ${\varvec{A}}$ be a full-rank $(n-k)\times n$ matrix over $\mathbb {F}_{q^m}$ and ${\varvec{x}}\in \mathbb {F}_{q^m}^{n-k}$ of rank w. Let ${\varvec{s}}= {\varvec{A}}{\varvec{x}}$. $({\varvec{A}},{\varvec{s}})$ is an instance of the $\mathsf {RSD}_{q,m,n,k,w}$ problem.

Let ${\varvec{S}}$ be a matrix obtained by the concatenation of N times the vector ${\varvec{s}}$. $({\varvec{A}},{\varvec{S}})$ is an instance of the $\mathsf {RSL}_{q,m,n,k,w,N}$ problem.

If we are able to solve any instances of the $\mathsf {RSL}_{q,m,n,k,w,N}$ problem, then we can recover the support of ${\varvec{x}}$ and solve the instance $({\varvec{A}},{\varvec{s}})$.

We can use this technique to solve any instances of the $\mathsf {RSD}_{q,m,n,k,w}$ problem, which proves that the $\mathsf {RSL}_{q,m,n,k,w,N}$ is as hard as the $\mathsf {RSD}_{q,m,n,k,w}$ problem in the worst case.

Security of the $\mathsf {DRSL}$ and $\mathsf {DRSD}$ Problems. We have already seen in the previous section that the $\mathsf {DRSD}$ problem is hard. As for other problems in cryptography (like DDH [7, 17]), the best known attacks on the $\mathsf {DRSL}_{q,m,n,k,w,N}$ problem consist in solving the same instance of the $\mathsf {RSL}_{q,m,n,k,w,N}$ problem, so we make the assumption that the $\mathsf {DRSL}_{q,m,n,k,w,N}$ problem is difficult.

Theorem 1

Under the assumption that $\mathsf {DRSL}$ is hard, the scheme ${\mathsf {RankPKE}}$ is semantically secure.

Proof

We proceed by a sequence of games.

$\mathbf{Game G }_0$ : This is the real $\mathsf {IND}$-$\mathsf {CPA}$ attack game. The ${\mathsf {RankPKE}}.{\mathsf {KeyGen}}$ is run and then, a 2-stage poly-time adversary $\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)$ is fed with the public key $pk =({\varvec{A}},{\varvec{p}},{\varvec{G}}')$. Then, $\mathcal {A}_1$ outputs a pair of messages $({\varvec{m}}_0,{\varvec{m}}_1)$. Next a challenge ciphertext is produced by flipping a coin b and producing a ciphertext $c^\star := (C^\star ,{\varvec{x}}^\star )$ of ${\varvec{m}}^\star ={\varvec{m}}_b$.

This ciphertext $c^\star$ comes from a random homogeneous matrix ${\varvec{U}}\in \mathbb {F}_{q^m}^{n\times n'}$ of weight w and then $c^\star = {\mathsf {RankPKE}}.{\mathsf {Enc}}(({\varvec{A}},{\varvec{p}},{\varvec{G}}'),{\varvec{m}}_b)$. On input $c^\star$, $\mathcal {A}_2$ outputs bit $b'$. We denote by $\textsf {S}_0$ the event $b'=b$ and use the same notation $\textsf {S}_n$ in any game $\mathbf{G}_n$ below.

$$\mathsf {Adv}^{\mathsf {ind}\textsf {-}\mathsf {cpa}}_{{\mathsf {RankPKE}}}(\mathcal A) = \mid 2\Pr [{ \textsf {S}}_0] - 1 \mid $$

$\mathbf{Game G }_1$ : In this game, we replace ${\varvec{p}}={\varvec{s}}A + {\varvec{e}}$ in ${\mathsf {RankPKE}}.{\mathsf {KeyGen}}$ by ${\varvec{p}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n}$. Under the hardness of the $\mathsf {DRSD}$ problem, the two games $\mathbf{G}_1$ and $\mathbf{G}_0$ are indistinguishable:

$$\left| \, \Pr [{ \textsf {S}}_1] - \Pr [{ \textsf {S}}_0] \,\right| \le \epsilon _\mathsf {drsd},$$

where $\epsilon _\mathsf {drsd}$ is the bound on the successful probability of the attacks against the problem $\mathsf {DRSD}$.

$\mathbf{Game G }_2$ : In this game, we replace $(C^\star ,{\varvec{x}}^\star )$ in $\mathbf{G}_1$ by $(C^\star \mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{(n-k)\times n'}, x^\star \mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n'})$.

As ${\varvec{x}}^\star$ is perfectly random, ${\varvec{x}}^\star - {\varvec{m}}^\star {\varvec{G}}$ is also perfectly random. In other words, this game replaces $\begin{pmatrix} {\varvec{A}}\\ \hline {\varvec{p}}\end{pmatrix} {\varvec{U}}= \begin{pmatrix} C^\star \\ \hline {\varvec{x}}^\star - {\varvec{m}}^\star {\varvec{G}} \end{pmatrix}$ by a perfectly random matrix. Therefore, the indistinguishability of the two games $\mathbf{G}_2$ and $\mathbf{G}_1$ follows from the hardness of the $\mathsf {DRSL}$ problem, applying it to the matrix ${\varvec{A}}' = \begin{pmatrix} {\varvec{A}} \\ \hline {\varvec{p}} \end{pmatrix}$ which is perfectly random because ${\varvec{A}}$ and ${\varvec{p}}$ are both perfectly random. Thus

$$\left| \, \Pr [{ \textsf {S}}_2] - \Pr [{ \textsf {S}}_1] \,\right| \le \epsilon _\mathsf {drsl},$$

where $\epsilon _\mathsf {drsl}$ is the bound on the successful probability of the attacks against the $\mathsf {DRSL}$ problem.

Advantage Zero. In this last game, as the ciphertext challenge $(C^\star ,{\varvec{x}}^\star )$ is perfectly random, b is perfectly hidden to any adversary $\mathcal {A}$.

$$\left| \, \Pr [{ \textsf {S}}_2] \,\right| = \frac{1}{2}$$

4 On the Difficulty of the Rank Support Learning Problem

The purpose of this section is to give some evidence towards the difficulty of the support learning problem $\mathsf {RSL}_{q,m,n,k,w,N}$ by

• explaining that it is the rank metric analogue of a problem in Hamming metric (the so called support learning problem) which has already been useful to devise signature schemes and for which after almost twenty years of existence only algorithms of exponential complexity are known;

• explaining that it is a problem which is provably hard for $N=1$ and that it becomes easy only for very large values of N;

• giving an algorithm which is the analogue in the rank metric of the best known algorithm for the support learning problem which is of exponential complexity. This complexity is basically smaller by a multiplicative factor which is only of order $q^{-\beta N}$ (for some $\beta <1$) than the complexity of solving the rank syndrome decoding problem $\mathsf {RSD}_{q,m,n,k,w}$;

• relating this problem to finding a codeword of rank weight w in a code where there are $q^N$ codewords of this weight. It is reasonable to conjecture that the complexity of finding such a codeword gets reduced by a multiplicative factor which is at most $q^N$ compared to the complexity of finding a codeword of rank weight w in a random code of the same length and dimension which has a single codeword of this weight;

• showing that this problem can also rephrased in terms of decoding a random code but defined over a larger alphabet ($\mathbb {F}_{q^{mN}}$ instead of $\mathbb {F}_{q^m}$).

4.1 A Related Problem: The Support Learning Problem

The rank support learning problem can be viewed as the rank metric analogue of the support learning problem which can be expressed as follows.

Problem 1

(Support Learning) . Let ${\varvec{A}}$ be a random full-rank matrix of size $(n-k)\times n$ over $\mathbb {F}_q$ and I be a subset of $\{1,\dots ,n\}$ of size w. Let V be the subspace of $\mathbb {F}_q^n$ of vectors with support I, that is the set of vectors ${\varvec{u}}=(u_i)_{1 \le i \le n} \in \mathbb {F}_q^n$ such that $u_i=0$ when $i \notin I$. Let $\mathcal {O}$ be an oracle which gives samples of the form $({\varvec{A}},{\varvec{A}}{\varvec{u}})$, where ${\varvec{u}}\mathop {\leftarrow }\limits ^{\$}V$. The support learning problem is to recover I given only access to the oracle.

We say that the problem is $(N,t,\varepsilon )$-hard if for every probabilistic algorithm $\mathcal {A}$ running in time t, we have

$$\begin{aligned} {{\mathrm{Prob}}}[\mathcal {A}({\varvec{A}},{\varvec{A}}{\varvec{U}}) = V] \leqslant \varepsilon ,\quad {\varvec{U}}\mathop {\leftarrow }\limits ^{\$}V^{ N} \end{aligned}$$

When we want to stress the fact that we care about the problem where we are allowed to make exactly N calls to the oracle, we denote this the $\mathsf {SL}_{q,n,k,w,N}$ problem. The pair $({\varvec{A}},{\varvec{A}}{\varvec{U}})$ is referred to as an instance of the $\mathsf {SL}_{q,n,k,w,N}$ problem.

When $N=1$ this is just the usual decoding problem of a random linear code with parity check matrix ${\varvec{A}}$. In this case, the problem is known to be NP-complete [5]. When N is greater than 1, this can be viewed as a decoding problem where we are given N syndromes of N errors which have a support included in the same set I. This support learning problem with $N>1$ has already been considered before in [34]. Its presumed hardness for moderate values of N was used there to devise a signature scheme [34], the so called KKS-scheme. Mounting a key attack in this case (that is for the Hamming metric) without knowing any signature that has been computed for this key really amounts to solve this support learning problem even it was not stated exactly like this in the article. However, when we have signatures originating from this scheme, the problem is of a different nature. Indeed, it was found out in [14] that signatures leak information. The authors showed there that if we know M signatures, then we are given ${\varvec{A}}$, ${\varvec{A}}{\varvec{U}}$ but also M vectors in $\mathbb {F}_q^n$, ${\varvec{v}}_1, \dots ,{\varvec{v}}_M$ whose support is included in I. The knowledge of those auxiliary ${\varvec{v}}_i$’s help a great deal to recover I : it suffices to compute the union of their support which is very likely to reveal the whole set I. When the ${\varvec{v}}_i$’s are random vectors in $\mathbb {F}_q^n$ of support included in I it is clearly enough to have a logarithmic number of them (in the size of the support I) to recover I. However this does not undermine the security of the support learning problem and just shows that the KKS-signature scheme is at best a one-time signature scheme.

Some progress on the support learning problem itself was achieved almost fifteen years later in [40]. Roughly speaking the idea there is to consider a code that has $q^N$ codewords of weight at most w which correspond to all possible linear combinations of the ${\varvec{u}}_i$’s and to use generic decoding algorithms of linear codes (which can also be used as low-weight codewords search algorithms) to recover one of those linear combinations. The process can then be iterated to reveal the whole support I. The fact that there are $q^N$ codewords of weight $\le w$ that are potential solutions for the low weight codeword search algorithm implies that we may expect to gain a factor of order $q^N$ in the complexity of the algorithm when compared to finding a codeword of weight w in a random linear code which has a single codeword of weight w. Actually the gain is less than this in practice. This seems to be due to the fact that we have highly correlated codewords (their support is for instance included in I). However, still there is some exponential speedup when compared to the single codeword case. This allowed to break all the parameters proposed in [34, 35] but also those of [4] which actually relied on the same problem. However, as has been acknowledged in [40], this does not give a polynomial time algorithm for the support learning problem, it just gives an exponential speedup when compared to solving a decoding problem with an error of weight w. The parameters of the KKS scheme can easily be chosen in order to thwart this attack.

4.2 Both Problems Reduce to Linear Algebra When N is Large Enough

As explained before when $N=1$ the support learning problem is NP-complete. The rank support learning problem is also hard in this case since it is equivalent to decoding in the rank metric an $\mathbb {F}_{q^m}$-linear code for which there is a randomized reduction to the NP-complete decoding problem in the Hamming metric [29]. It is also clear that both problems become easy when N is large enough and for the same reason : they basically amount to compute a basis of a linear space.

In the Hamming metric, this corresponds to the case when $N=w$. Indeed in this case, notice that the dimension of the subspace V is w. When the ${\varvec{u}}_i$’s are generated randomly with support included in I they have a constant probability K(q) (which is increasing with q and bigger than 0.288 in the binary case) to generate the space ${\varvec{A}}V$. Once we know this space, the problem becomes easy. Indeed let ${\varvec{e}}_1,\dots ,{\varvec{e}}_n$ be the canonical generators of $\mathbb {F}_q^n$ (i.e. ${\varvec{e}}_i$ has only one non-zero entry which is its i-th entry that is equal to 1). We recover I by checking for all positions i in $\{1,\dots ,n\}$ whether ${\varvec{A}}{\varvec{e}}_i$ belongs to ${\varvec{A}}V$ or not. If it is the case, then i belongs to I, if this is not the case, i does not belong to I.

There is a similar algorithm for the rank support learning problem. This should not come as a surprise since supports of code positions for the Hamming metric really correspond to subspaces of $\mathbb {F}_{q^m}$ for the rank metric metric as has been put forward in [27] (see also [33] for more details about this). The difference being however that we need much bigger values of N to mount a similar attack to the Hamming metric case. Indeed what really counts here is the space that can be generated by the ${\varvec{A}}{\varvec{u}}_i$’s where the ${\varvec{u}}_i$’s are the columns of ${\varvec{U}}$. It is nothing but the space ${\varvec{A}}V^n$. Let us denote this space by W. This space is not $\mathbb {F}_{q^m}$-linear, however it is $\mathbb {F}_q$-linear and it is of dimension nw viewed as an $\mathbb {F}_q$-linear subspace of $\mathbb {F}_{q^m}^n$. When $N=nw$ we can mount a similar attack, namely we compute the space generated by linear combinations over $\mathbb {F}_q$ of ${\varvec{A}}{\varvec{u}}_1,\dots , {\varvec{A}}{\varvec{u}}_{nw}$. They generate W with constant probability K(q). When we look all $\mathbb {F}_q$-linear subspaces $V'$ of $\mathbb {F}_{q^m}$ of dimension 1 (there are less than $q^m$ of them) and check whether the subspace $W'$ of dimension n given by ${\varvec{A}}V'^n$ is included in $W={\varvec{A}}V^n$ or not. By taking the sum of the spaces for which this is the case we recover V. Actually the complexity of this algorithm can be improved by using in a more clever way the knowledge of W, but this is beyond the scope of this article and this algorithm is just here to explain the deep similarities between both cases and to convey some intuition about when the rank support learning problem becomes easy.

This discussion raises the issue whether there is an algorithm “interpolating” standard decoding algorithms when $N=1$ and linear algebra when $N=w$ in the Hamming metric case and $N=nw$ in the rank metric case. This is in essence what has been achieved in [40] for the Hamming metric and what we will do now here for the rank metric.

4.3 Solving the Subspace Problem with Information-Set Decoding

There are two ingredients in the algorithm for solving the support learning problem in [40]. The first one is to set up an equivalent problem which amounts to find a codeword of weight $\le w$ in a code which has $q^N$ codewords of this weight. The second one is to use standard information set decoding techniques to solve this task and to show that it behaves better than in the case where there is up to a multiplicative constant a single codeword of this weight in the code. We are going to follow the same route here for the rank metric.

We begin by introducing the following $\mathbb {F}_q$-linear code

$${\mathcal {C}}\mathop {=}\limits ^{\text {def}}\{ {\varvec{x}}\in \mathbb {F}_{q^m}^n: {\varvec{A}}{\varvec{x}}\in W_U \}$$

where $W_U$ is the $\mathbb {F}_q$-linear subspace of $\mathbb {F}_{q^m}^{n-k}$ generated by linear combinations of the form $\sum _i \alpha _i {\varvec{A}}{\varvec{u}}_i$ where $\alpha _i$ belongs to $\mathbb {F}_q$ and the ${\varvec{u}}_i$’s are the N column vectors forming the matrix ${\varvec{U}}$. This code has the following properties.

Lemma 1

Let ${\mathcal {C}}' \mathop {=}\limits ^{\text {def}}\{ \sum _i \alpha _i {\varvec{u}}_i: \alpha _i \in \mathbb {F}_q\}$. We have

• 1. $\dim _{\mathbb {F}_q} {\mathcal {C}}\le km+N$

• 2. ${\mathcal {C}}' \subset {\mathcal {C}}$

• 3. all the elements of ${\mathcal {C}}'$ are of rank weight $\le w$.

[27] gives several algorithms for decoding $\mathbb {F}_{q^m}$-linear codes for the rank metric. The first one can be generalized in a straightforward way to codes which are just $\mathbb {F}_q$-linear as explained in more detail in [33]. This article also explains how this algorithm can be used in a straightforward way to search for low rank codewords in such a code. Here our task is to look for codewords of rank $\le w$ which are very likely to lie in ${\mathcal {C}}'$ which would reveal a linear combination ${\varvec{c}}= \sum _i \alpha _i {\varvec{u}}_i$. This reveals in general V when ${\varvec{c}}$ is of rank weight w simply by computing the vector space over $\mathbb {F}_q$ generated by the entries of ${\varvec{c}}$. When the rank of ${\varvec{c}}$ is smaller this yields a subspace of V and we will discuss later on how we finish the attack.

Let us concentrate now on analyzing how the first decoding algorithm of [27] behaves when we use it to find codewords of ${\mathcal {C}}$ of rank $\le w$. For this, we have to recall how the support attack of [27] works.

We assume that we want to find a codeword of weight w in an $\mathbb {F}_q$-linear code which is a $\mathbb {F}_q$-subspace of $\mathbb {F}_{q^m}$ of dimension K. For the purpose of this algorithm, a codeword ${\varvec{c}}=(c_1,\dots ,c_n) \in \mathbb {F}_{q^m}^n$ is also viewed as a matrix $(c_{ij})_{\begin{array}{c} 1 \le i \le m \\ 1 \le j \le n \end{array}}$ over $\mathbb {F}_q$ by writing the $c_i$’s in a arbitrary $\mathbb {F}_q$ basis $(\beta _1,\dots ,\beta _m)\in \mathbb {F}_{q^m}^m$ of $\mathbb {F}_{q^m}$ viewed as vector space over $\mathbb {F}_q$: $c_i = \sum _{j=1}^m c_{ij}\beta _j.$ There are $nm-K$ linear equations which specify the code that are satisfied by the $c_{ij}$’s of the form

$$\begin{aligned} \sum _{1 \le i,j \le m} h^{s}_{ij} c_{ij}=0 \end{aligned}$$

(1)

for $s={1,\dots ,mn-K}$. Algorithm 1 explains how a codeword of weight $\le w$ is produced by the approach of [27]. The point of choosing r like this in this algorithm, i.e.

$$\begin{aligned} r \mathop {=}\limits ^{\text {def}}m - \left\lceil \frac{K}{n} \right\rceil \end{aligned}$$

(2)

is that r is the smallest integer for which the linear system (3) has more equations than unknowns (and we therefore expect that it has generally only the all-zero solution).

Theorem 2

Assume that $w \le \min \left( \left\lfloor \frac{K}{n} \right\rfloor ,\left\lfloor \frac{N}{n} \right\rfloor +1\right)$ and that $\frac{w + \left\lfloor \frac{K}{n} \right\rfloor }{2} \ge \left\lfloor \frac{N}{n} \right\rfloor$. Let

$$\begin{aligned} e_{-}= & {} \left( w-\left\lfloor \frac{N}{n}\right\rfloor \right) \left( \left\lfloor \frac{K}{n}\right\rfloor - \left\lfloor \frac{N}{n}\right\rfloor \right) \\ e_{+}= & {} \left( w-\left\lfloor \frac{N}{n}\right\rfloor -1\right) \left( \left\lfloor \frac{K}{n}\right\rfloor - \left\lfloor \frac{N}{n}\right\rfloor -1\right) +n \left( \left\lfloor \frac{N}{n}\right\rfloor + 1\right) -N \end{aligned}$$

Algorithm 1 outputs an element of ${\mathcal {C}}'$ with complexity $\tilde{\mathcal {O}}\big ( q^{\min (e_{-},e_{+})} \big )$. We give the complete proof of this theorem in the the full version of this paper [26].

Remark 2

• 1. When N and $K=km+N$ are multiple of n, say $N=\delta n$ and $K= \alpha R n+\delta$ (with $\alpha \mathop {=}\limits ^{\text {def}}\frac{m}{n}$, $R=\frac{k}{n}$) the complexity above simplifies to $\tilde{\mathcal {O}}\big ( q^{\alpha R n(w-\delta )} \big )$. In other words the complexity gets reduced by a factor $q^{\alpha R \delta n}=q^{\alpha R N}$ when compared to finding a codeword of weight w in a random $\mathbb {F}_q$-linear code of the same dimension and length.

• 2. This approach is really suited to the case $m \le n$. When $m >n$ we obtain better complexities by working on the transposed code (see [33] for more details about this approach).

4.4 Link Between Rank Support Learning and Decoding over the Rank Metric

We have exploited here that for solving the rank support learning problem, it can be rephrased in terms of finding a codeword of low rank weight in a code that has many codewords of such low rank weight (namely the code ${\mathcal {C}}$ that has been introduced in this section). ${\mathcal {C}}$ is not a random code however, it is formed by a random subcode, namely the code ${\mathcal {C}}_0 =\{{\varvec{x}}\in \mathbb {F}_{q^m}^n: {\varvec{A}}{\varvec{x}}=0\}$ plus some non random part, namely ${\mathcal {C}}'$ which contains precisely the low rank codeword we are after. In other words ${\mathcal {C}}$ decomposes as

$$ {\mathcal {C}}= {\mathcal {C}}_0 \oplus {\mathcal {C}}' $$

where ${\mathcal {C}}_0$ is a truly random code and ${\mathcal {C}}'$ is a subcode of ${\mathcal {C}}$ that contains the codewords of ${\mathcal {C}}$ of low-rank. ${\mathcal {C}}$ is therefore not really a random code.

There is a way however to rephrase the rank support learning problem as a problem of decoding a random code. The trick is to change the alphabet of the code. We define the code ${\mathcal {C}}_{N}$ as

$$ {\mathcal {C}}_{N}= \{ {\varvec{x}}\in \mathbb {F}_{q^{mN}}: {\varvec{A}}{\varvec{x}}=0\}. $$

In other words, ${\mathcal {C}}_{N}$ is a code defined over the extension field $\mathbb {F}_{q^{mN}}$ but with a random parity-check matrix with entries defined over $\mathbb {F}_{q^m}$.

There are several ways to equip $\mathbb {F}_{q^{mN}}^n$ with a rank metric. One of them consists in writing the entries $c_i$ of a codeword ${\varvec{c}}= (c_1,\dots ,c_n) \in \mathbb {F}_{q^{mN}}^n$ of ${\mathcal {C}}_{N}$ as column vectors $(c_{ij})_{1 \le j \le mN} \in \mathbb {F}_q^{mN}$ by expressing the entry $c_i$ in a $\mathbb {F}_q$ basis of $\mathbb {F}_{q^{mN}}$ $(\beta _1,\dots ,\beta _{mN})$, i.e. $c_i = \sum _{1 \le j \le mN} c_{ij} \beta _j$ and replacing each entry by the corresponding vector to obtain an $mN \times n$ matrix. The rank of this matrix would then define the rank weight of a codeword. However, since $\mathbb {F}_{q^{mN}}$ is an extension field of $\mathbb {F}_{q^m}$ there are also other ways to define a rank metric. We will choose the following one here. First we decompose each entry $c_i$ in an $\mathbb {F}_{q^m}$-basis $(\gamma _1,\dots ,\gamma _{N})$ of $\mathbb {F}_{q^{mN}}$:

$$ c_i = \sum _{j=1}^N \alpha _{(i-1)N+j} \gamma _j $$

where the $\alpha _i$’s belong to $\mathbb {F}_{q^m}$. The rank weight of $(c_1,\dots ,c_n)$ is then defined as the rank weight of the vector $(\alpha _i)_{1 \le i \le nN} \in \mathbb {F}_{q^m}^{nN}$ where the rank weight of the last vector is defined as we have done up to here, namely by replacing each entry $\alpha _i$ by a column vector $(\alpha _{ij})_{1 \le j \le m}$ obtained by taking the coordinates of $\alpha _i$ in some $\mathbb {F}_q$-basis of $\mathbb {F}_{q^m}$. In other words, the rank weight of $(c_1,\dots ,c_n)$ is defined as the rank of the associated $m \times nN$ matrix.

Let us now introduce the rank decoding problem with random parity check matrices defined over a smaller field.

Definition 8

(Rank Decoding with parity-check matrices defined over a subfield ($\mathsf {RDPCSF}$)). Let ${\varvec{A}}$ be a random full-rank matrix of size $(n-k)\times n$ over $\mathbb {F}_{q^m}$ and ${\varvec{e}}\in \mathbb {F}_{q^{mN}}^n$ be a random word of rank weight w. The $\mathsf {RDPCSF}_{q,m,n,k,w,N}$ problem is to recover ${\varvec{e}}$ from the knowledge of ${\varvec{A}}\in \mathbb {F}_{q^m}^{(n-k) \times n}$ and ${\varvec{A}}{\varvec{e}}\in \mathbb {F}_{q^{mN}}^{n-k}$.

It turns out that the support learning problem and the rank decoding problem with parity-check matrices defined over a smaller field are equivalent

Theorem 3

The problems $\mathsf {RSL}_{q,m,n,w,N}$ and $\mathsf {RDPCSF}_{q,m,n,w,N}$ are equivalent : any randomized algorithm solving one of this problem with probability $\ge \epsilon$ in time t can be turned into an algorithm for the other problem solving it with probability $\ge \epsilon$ in time $t+P(q,m,n,w,N)$, where P is a polynomial function of its entries.

Proof

Let us consider an instance $({\varvec{A}},{\varvec{A}}{\varvec{U}})$ of the $\mathsf {RSL}_{q,m,n,w,N}$ problem. Denote the j-th column of ${\varvec{U}}$ by ${\varvec{u}}_j$. Define now ${\varvec{e}}\in \mathbb {F}_{q^{mN}}^n$ by ${\varvec{e}}= \sum _{j=1}^N \gamma _j {\varvec{u}}_j$, where $(\gamma _1,\dots ,\gamma _N)$ is some $\mathbb {F}_{q^m}$-basis of $\mathbb {F}_{q^{mN}}$. From the definition of the rank weight we have chosen over $\mathbb {F}_{q^{mN}}^n$, it is clear that the rank weight of ${\varvec{e}}$ is less than or equal to w. The pair $(A,\sum _{j=1}^N \gamma _j {\varvec{A}}{\varvec{u}}_j)$ is then an instance of the $\mathsf {RDPCSF}_{q,m,n,w,N}$ problem. It is now straightforward to check that we transform in this way a uniformly distributed instance of the $\mathsf {RSL}_{q,m,n,w,N}$ problem into a uniformly distributed instance of the $\mathsf {RDPCSF}_{q,m,n,w,N}$ problem. The aforementioned claim on the equivalence of the two problems follows immediately from this and the fact that when we know the space generated by the entries of the ${\varvec{u}}_j$’s, we just have to solve a linear system to recover a solution of the decoding problem (this accounts for the additive polynomial overhead in the complexity).

Note that this reduction of the rank support learning problem to the problem of decoding a linear code over an extension field $\mathbb {F}_{q^{mN}}$ defined from a random parity-check matrix defined over the base field $\mathbb {F}_{q^m}$ works also for the Hamming metric : the support learning problem $\mathsf {SL}_{q,n,w,N}$ also reduces to decoding a linear code over an extension field $\mathbb {F}_{q^{mN}}$ defined from a random parity-check matrix defined over the base field $\mathbb {F}_{q^m}$ but this time for the Hamming metric over $\mathbb {F}_{q^{mN}}^n$. All these considerations point towards the same direction, namely that when N is not too large, the rank support learning problem should be a hard problem. It is for instance tempting to conjecture that this problem can not be solved $q^N$ faster than decoding errors of rank weight w for an [n, k] random linear code over $\mathbb {F}_{q^m}$. A similar conjecture could be made for the support learning problem.

5 Identity Based Encryption

Identity-based encryption schemes. An identity-based encryption (${\mathsf {IBE}}$) scheme is a tuple of algorithms providing the following functionality. The trusted authority runs ${\mathsf {Setup}}$ to generate a master key pair (mpk, msk). It publishes the master public key mpk and keeps the master secret key msk private. When a user with identity $ID$ wishes to become part of the system, the trusted authority generates a user decryption key $d _ ID \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {KeyDer}}(msk, ID )$, and sends this key over a secure and authenticated channel to the user. To send an encrypted message $m$ to the user with identity $ID$, the sender computes the ciphertext $C \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {Enc}}(mpk, ID , m )$, which can be decrypted by the user as $m \leftarrow {\mathsf {Dec}}( d _ ID , C )$. We refer to [10] for details on the security definitions for IBE schemes.

Security. We define the security of ${\mathsf {IBE}}$ schemes through a game with an adversary. In the first phase, the adversary is run on input of the master public key of a freshly generated key pair $(mpk,msk) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {Setup}}$. In a chosen-plaintext attack ($\mathsf {IND}-\mathsf {CPA}$), the adversary is given access to a key derivation oracle $\mathcal {O}$ that on input an identity returns . At the end of the first phase, the adversary outputs two equal-length challenge messages and a challenge identity . The adversary is given a challenge ciphertext for a randomly chosen bit b, and is given access to the same oracle $\mathcal {O}$ as during the first phase of the attack. The second phase ends when the adversary outputs a bit $b'$. The adversary is said to win the $\mathsf {IND}-\mathsf {CPA}$ game if $b'=b$ and if it never queried the key derivation oracle for the keys of any identity that matches the target identity.

Definition 9

An ${\mathsf {IBE}}$ scheme is $\mathsf {IND}-\mathsf {CPA}$-secure if any poly-time adversary $\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)$ making at most a polynomial number of queries to the key derivation oracle, only has a negligible advantage in the $\mathsf {IND}-\mathsf {CPA}$ game described above, i.e., the following advantage is negligible:

$$2 \times \Pr \left[ \begin{array}{l} (mpk, msk) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {Setup}}, ( ID , m_0,m_1,s)\leftarrow \mathcal {A}_1^{\mathcal {O}}(mpk), \\ b\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}, c={\mathsf {Enc}}({ mpk }, ID ,(m_b)): \mathcal {A}_2^{\mathcal {O}}(m_0,m_1,s,c) = b \end{array} \right] - 1.$$

5.1 Trapdoor Functions from RankSign

We now adapt the RankSign system to construct a trapdoor function, which is sufficient to convert our PKE to an IBE. Associated to a matrix ${\varvec{A}}\in \mathbb {F}_{q^m}^{(n-k)\times n}$, we define the function $f_{{\varvec{A}}}$ as follows:

$$\begin{aligned} f_{{\varvec{A}}}: \mathbb {F}_{q^m}^{n-k} \times \mathbb {F}_{q^m}^{n}\rightarrow & {} \mathbb {F}_{q^m}^{n}\\ ({\varvec{s}},{\varvec{e}})\mapsto & {} {\varvec{s}}{\varvec{A}}+{\varvec{e}}\end{aligned}$$

The matrix ${\varvec{A}}$ will be generated with a trapdoor ${\varvec{T}}$ such that $f_{{\varvec{A}}}$ is a trapdoor function: from a random ${\varvec{p}}\in \mathbb {F}_{q^m}^{n}$, with the trapdoor ${\varvec{T}}$, one can sample $({\varvec{s}},{\varvec{e}}) = f_{{\varvec{A}}}^{-1}({\varvec{p}})$ such that ${\varvec{e}}$ is indistinguishable from a random element in $W_r$, the set of all the words of rank r and of length n, as defined in ${\mathsf {RankPKE}}$. These properties will be sufficient for us to construct an IBE and reduce its security to the security of ${\mathsf {RankPKE}}$. We now describe how we can get such a trapdoor function by relying on the RankSign system [28].

RankSign. RankSign is a signature scheme based on the rank metric. Like other signature schemes based on coding theory [16], RankSign needs a family of codes with an efficient decoding algorithm. It takes on input a random word of the syndrome space (obtained from the hash of the file we want to sign) and outputs a word of small weight with the given syndrome. This is an instance of the $\mathsf {RSD}$ problem, with the difference that the matrix ${\varvec{H}}$ has a trapdoor which makes the problem easy. The public key is a description of the code which hides its structure and the secret key, on the contrary, reveals the structure of the code, which allows the signer to solve the $\mathsf {RSD}$ problem. RankSign does not compute a codeword of weight below the Gilbert-Varshamov bound, but instead a codeword of weight r between the Gilbert-Varshamov bound and the Singleton bound. The idea is to use a family of the augmented Low Rank Parity Check codes (denoted $LRPC^+$), and an adapted decoding algorithm (called the General Errors/Erasures Decoding algorithm) to produce such a codeword from any syndrome. The decoding algorithm is probabilistic and the parameters of the code have to be chosen precisely in order to have a probability of success very close to 1. We refer to [28] for a complete description of the decoding algorithm and the signature algorithm.

Definition 10

(Augmented Low Rank Parity Check Codes). Let ${\varvec{H}}$ be an $\mathbb {F}_{q^m}^{(n-k)\times n}$ homogeneous matrix of full-rank and of weight d and ${\varvec{R}}\in \mathbb {F}_{q^m}^{(n-k)\times t}$ be a random matrix. Let ${\varvec{P}}\in GL_{n-k}(\mathbb {F}_{q^m})$ and ${\varvec{Q}}\in GL_{n+t}(\mathbb {F}_q)$ be two invertible matrices (remark that the coefficients of ${\varvec{Q}}$ belong to the base field). Let ${\varvec{H}}' = {\varvec{P}}({\varvec{R}}|{\varvec{H}}) {\varvec{Q}}$ be the parity-check matrix of a code ${\mathcal {C}}$ of type $[n+t,t+k]$. By definition, such a code is an $LRPC^+$ code. If $t = 0$, ${\mathcal {C}}$ is an LRPC code.

The public key of RankSign is the matrix ${\varvec{H}}'$, the secret key is the structured matrix $({\varvec{R}}|{\varvec{H}})$ and the trapdoor is the pair of matrices $({\varvec{P}},{\varvec{Q}})$.

We can now describe the trapdoor function $f_{{\varvec{A}}}^{-1}$. Let ${\varvec{p}}\in \mathbb {F}_{q^m}^{n+t}$ and ${\varvec{H}}'$ the public key of an instance of RankSign. We choose ${\varvec{A}}$ as a generator matrix of a code with parity-check matrix ${\varvec{H}}'$, i.e. as a full-rank matrix over $\mathbb {F}_{q^m}$ of size $(k+t) \times (n+t)$ which is such that ${\varvec{H}}' {\varvec{A}}^T = 0$. First, we compute ${\varvec{H}}'{\varvec{p}}$ and then we apply RankSign with trapdoor T to this syndrome to obtain a vector ${\varvec{e}}$ of weight r such that ${\varvec{H}}'{\varvec{p}}^T = {\varvec{H}}'{\varvec{e}}^T$. Finally, we solve the linear system ${\varvec{s}}{\varvec{A}}= {\varvec{p}}- {\varvec{e}}$ of unknown ${\varvec{s}}$ and the secret key associated to ${\varvec{p}}$ is set to be ${\varvec{s}}$. The security of the RankSign system is based on the assumption that ${\varvec{H}}'$ is computationally indistinguishable from a random matrix.

Definition 11

( $\mathsf {LRPC^+}$ problem [28]). Given an augmented LRPC code, distinguish it from a random code with the same parameters.

The hardness of this problem is studied in [28]. Currently the best attacks consist in recovering the structure of the LRPC by looking for small-weight words in the code, and the best algorithms for that are generic algorithms whose complexity is exponential [33].

Proposition 3

Let ${\varvec{H}}'$ be a public RankSign matrix and ${\varvec{A}}$ be a generator matrix of the associated code. The two following distributions are computationally indistinguishable:

Let $\mathcal {D}_0$ the distribution $({\varvec{p}},{\varvec{s}},{\varvec{e}})$ where ${\varvec{p}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n+t}$, ${\varvec{e}}\in W_r$ is sampled from RingSign Algorithm such that ${\varvec{H}}'{\varvec{e}}^T = {\varvec{H}}'{\varvec{p}}^T$ and ${\varvec{s}}$ is the solution of the linear system ${\varvec{x}}{\varvec{A}}= {\varvec{p}}- {\varvec{e}}$ of unknown ${\varvec{x}}$.

Let $\mathcal {D}_1$ be the distribution $({\varvec{p}}', {\varvec{s}}', {\varvec{e}}')$ with ${\varvec{s}}' \mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{k+t}$, ${\varvec{e}}' \mathop {\leftarrow }\limits ^{\$}W_r$ and ${\varvec{p}}' = {\varvec{s}}'{\varvec{A}}+{\varvec{e}}'$.

Precisely, the maximum advantage $\epsilon$ of the adversaries to distinguish $\mathcal {D}_0$ et $\mathcal {D}_1$ is bounded by: $\epsilon \le \frac{2}{q} + \epsilon _{\mathsf {drsd}}$

Proof

Let $\mathcal {D}_2$ be the distribution $({\varvec{s}},{\varvec{e}})$ where ${\varvec{s}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n-k}$ and ${\varvec{e}}$ is a signature of ${\varvec{s}}$ by RankSign with the public key ${\varvec{H}}'$ (i.e., $\Vert {\varvec{e}} \Vert = r$ and ${\varvec{H}}'{\varvec{e}}^T = {\varvec{s}}$). Let $\mathcal {D}_3$ be the distribution $({\varvec{H}}'{\varvec{e}}'^T, {\varvec{e}}'^T)$ with ${\varvec{e}}' \mathop {\leftarrow }\limits ^{\$}W_r$.

According to the proof of Theorem 2 of [28], a sample $({\varvec{H}}'{\varvec{e}}'^T, {\varvec{e}}'^T) \leftarrow \mathcal {D}_3$ is distributed exactly as $\mathcal {D}_2$ except if $({\varvec{H}}'{\varvec{e}}'^T, {\varvec{e}}'^T)$ is not T-decodable and the probability that the latter occurs is less than $\frac{2}{q}$. Therefore an adversary can not distinguish $\mathcal {D}_2$ from $\mathcal {D}_3$ with an advantage larger than $\frac{2}{q}$.

Now, we can prove the proposition. First, let us examine the distribution $\mathcal {D}_0$. Since ${\varvec{H}}'$ is a linear map and ${\varvec{p}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{n+t}$, ${\varvec{s}}= {\varvec{H}}'{\varvec{p}}^T$ is uniformly distributed among $\mathbb {F}_{q^m}^{n-k}$. This implies $(\varvec{\sigma }, {\varvec{e}}) \leftarrow \mathcal {D}_2$. Moreover, ${\varvec{p}}- {\varvec{e}}$ is uniformly distributed among the words of the code generated by ${\varvec{A}}$, hence ${\varvec{s}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{k+t}$.

According to the indistinguishability of $\mathcal {D}_2$ and $\mathcal {D}_3$, the distribution of ${\varvec{e}}'$ and ${\varvec{e}}$ are computationally indistinguishable. ${\varvec{s}}'$ and ${\varvec{s}}$ are both uniformly distributed. Finally, based on the assumption that the DRSD problem is hard, ${\varvec{p}}'$ and ${\varvec{p}}$ are indistinguishable.

Summing up these two steps, the advantage of an adversary to distinguish $\mathcal {D}_0$ from $\mathcal {D}_1$ is bounded by $\frac{2}{q} + \epsilon _{\mathsf {drsd}}$.    $\square$

5.2 Scheme

Our IBE system uses a random oracle H which maps the identity into the public keys space $\mathbb {F}_{q^m}^{n+t}$ of our encryption scheme.

• ${\mathsf {IBE}}.{\mathsf {Setup}}$

  • choose the parameters (n, m, k, d, t) of the scheme according to RankSign. The secret master key is the triplet of matrices ${\varvec{P}}, ({\varvec{R}}|{\varvec{H}})$ and ${\varvec{Q}}$ such that ${\varvec{H}}$ is a parity-check matrix of an [n, k] LRPC code of weight d over $\mathbb {F}_{q^m}$, ${\varvec{R}}\mathop {\leftarrow }\limits ^{\$}\mathbb {F}_{q^m}^{(n-k)\times t}$, ${\varvec{P}}\mathop {\leftarrow }\limits ^{\$}GL_{n-k}(\mathbb {F}_{q^m})$ and ${\varvec{Q}}\mathop {\leftarrow }\limits ^{\$}GL_{n+t}(\mathbb {F}_q)$. Let ${\varvec{A}}$ be a full rank $(k+t) \times (n+t)$ matrix over $\mathbb {F}_{q^m}$ such ${\varvec{H}}' {\varvec{A}}^T = 0$ with ${\varvec{H}}' = {\varvec{P}}({\varvec{R}}|{\varvec{H}}){\varvec{Q}}$ and the trapdoor ${\varvec{T}}$ is $({\varvec{P}},{\varvec{Q}})$.

  • define ${\varvec{G}}\in \mathbb {F}_{q^m}^{k'\times n'}$ to be a generator matrix of a public code ${\mathcal {C}}'$ which can decode (efficiently) errors of weight up to wr as in ${\mathsf {RankPKE}}.{\mathsf {KeyGen}}$.

  • return $mpk=({\varvec{A}},{\varvec{G}})$ and $msk={\varvec{T}}$

• ${\mathsf {IBE}}.{\mathsf {KeyDer}}({\varvec{A}},{\varvec{T}},id)$ :

  • compute ${\varvec{p}}= H(id)$

  • compute $({\varvec{s}},{\varvec{e}})= f^{-1}_{{\varvec{A}}}({\varvec{p}})$ by using the trapdoor ${\varvec{T}}$

  • store $(id,{\varvec{s}})$ and return ${\varvec{s}}$

• ${\mathsf {IBE}}.{\mathsf {Enc}}(id,{\varvec{m}})$ :

  • compute ${\varvec{p}}= H(id)$

  • return ${\varvec{c}}= {\mathsf {RankPKE}}.{\mathsf {Enc}}(({\varvec{A}},{\varvec{p}},{\varvec{G}}),{\varvec{m}})$

• ${\mathsf {IBE}}.{\mathsf {Dec}}({\varvec{s}},{\varvec{c}})$ : return ${\mathsf {RankPKE}}.{\mathsf {Dec}}({\varvec{s}},{\varvec{c}})$.

5.3 Security

We now state the security of the ${\mathsf {IBE}}$ system.

Theorem 4

Under the assumption that the $\mathsf {LRPC^+}$ problem is hard and the ${\mathsf {RankPKE}}$ is secure, the ${\mathsf {IBE}}$ system described above is $\mathsf {IND}-\mathsf {CPA}$-secure in the random oracle model:¹

$$\epsilon _\mathsf {ibe}\le \frac{2q_H}{q} + \epsilon _\mathsf {lrpc^+}+ q_H( \epsilon _\mathsf {drsd}+ \epsilon _\mathsf {pke})$$

where $\epsilon _\mathsf {lrpc^+}, \epsilon _\mathsf {pke}, \epsilon _\mathsf {ibe}$ are respectively the bound on the advantage of the attacks against the $\mathsf {LRPC^+}$ problem, the ${\mathsf {RankPKE}}$ system and the ${\mathsf {IBE}}$ system, and $q_H$ is the maximum number of distinct hash queries to H that an adversary can make.

Proof

We proceed by a sequence of games.

$\mathbf{Game G }_0$ : This is the real $\mathsf {IND}$-$\mathsf {CPA}$ attack game. The ${\mathsf {IBE}}.{\mathsf {Setup}}$ is run and then, a 2-stage poly-time adversary $\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)$ is fed with the public key $mpk=({\varvec{A}},{\varvec{G}})$. $\mathcal {A}_1$ can ask queries to H and key queries. Then, $\mathcal {A}_1$ outputs a challenge identity $id^\star$, which is different from the key queries $\mathcal {A}_1$ already asked, and a pair of messages $({\varvec{m}}_0,{\varvec{m}}_1)$. Next a challenge ciphertext is produced by flipping a coin b and producing a ciphertext $c^\star = {\mathsf {IBE}}.{\mathsf {Enc}}(id^\star ,{\varvec{m}}_b)$.

On input $c^\star$, $\mathcal {A}_2$ can continue to ask queries to H and key queries which are different from $id^\star$, and finally outputs bit $b'$. We denote by $\textsf {S}_0$ the event $b'=b$ and use the same notation $\textsf {S}_n$ in any game $\mathbf{G}_n$ below.

$$ \mathsf {Adv}^{\mathsf {ind}\textsf {-}\mathsf {cpa}}_{{\mathsf {IBE}}}(\mathcal A) = \mid 2\Pr [{ \textsf {S}}_0] - 1 \mid $$

We assume without loss of generality that, for any identity id that $\mathcal {A}$ wants to corrupt, $\mathcal {A}$ already queried H on id. In particular, we can assume that $\mathcal {A}$ will query the challenge identity $id^\star$ to H.

As this is the real attack game, for a key query on an identity id, the ${\mathsf {IBE}}.{\mathsf {KeyDer}}({\varvec{A}},{\varvec{T}},id)$ is run and the secret key is given to $\mathcal {A}$. We recall this algorithm:

• compute ${\varvec{p}}= H(id)$

• compute $({\varvec{s}},{\varvec{e}})= f^{-1}_{{\varvec{A}}}({\varvec{p}})$ by using the trapdoor ${\varvec{T}}$:

  • compute ${\varvec{H}}'{\varvec{p}}$ and then we apply RankSign with trapdoor ${\varvec{T}}$ to this syndrome to obtain a vector ${\varvec{e}}$ of weight r such that ${\varvec{H}}'{\varvec{p}}= {\varvec{H}}'{\varvec{e}}$.

  • solve the linear system ${\varvec{s}}{\varvec{A}}= {\varvec{p}}- {\varvec{e}}$ of unknown ${\varvec{s}}$ and the secret key associated to ${\varvec{p}}$ is set to be ${\varvec{s}}$.

• store $(id,{\varvec{s}})$ and return ${\varvec{s}}$.

$\mathbf{Game G }_1$ : In this game, we modify the answers to the key queries so that it does not require the trapdoor ${\varvec{T}}$ anymore. In order to make the answers coherent, we also need to simulate the queries to the hash queries to H. We maintain a list $\mathsf {List}_H$, initially set to empty, to store the tuples $(id,{\varvec{p}},{\varvec{s}})$ where ${\varvec{p}}$ is the value that we respond to the H query on id, and ${\varvec{s}}$ is the secret key which corresponds to the public key ${\varvec{p}}$ we generate. The simulation is given in the following way:

• Hash queries: on $\mathcal {A}$’s jth distinct query $id_j$ to H:

  • randomly choose a vector ${\varvec{e}}_j$ of weight r

  • randomly choose ${\varvec{s}}_j$

  • define ${\varvec{p}}_j=H(id)={\varvec{s}}_j{\varvec{A}}+ {\varvec{e}}_j$

  • add the tuple $(id_j,{\varvec{p}}_j,{\varvec{s}}_j)$ to $\mathsf {List}_H$ and return ${\varvec{p}}_j$ to $\mathcal {A}$.

• Secret key queries: when $\mathcal {A}$ asks for a secret key for the identity id, we retrieve the tuple $(id, {\varvec{p}}, {\varvec{s}})$ from the $\mathsf {List}_H$ and return ${\varvec{s}}$ to $\mathcal {A}$.

Now, looking back at the Proposition 3, we remark that the set of $q_H$ samples $({\varvec{p}}_j,{\varvec{s}}_j,{\varvec{e}}_j)$ in the previous game come from the distribution $\mathcal {D}_0^{q_H}$ and the set of $q_H$ samples $({\varvec{p}}_j,{\varvec{s}}_j,{\varvec{e}}_j)$ in this game come from the distribution $\mathcal {D}_1^{q_H}$. We thus have:

$$\left| \, \Pr [{ \textsf {S}}_1] - \Pr [{ \textsf {S}}_0] \,\right| \le \frac{2q_H}{q} + q_H \epsilon _\mathsf {drsd}$$

$\mathbf{Game G }_2$ : As the objective is to reduce the security of the ${\mathsf {IBE}}$ to the security of ${\mathsf {RankPKE}}$, in this game, we define the matrix ${\varvec{A}}$ to be a random matrix as in the ${\mathsf {RankPKE}}$. Because the simulation in the previous game does not use the trapdoor ${\varvec{T}}$, we can keep the simulation for hash queries and key queries exactly unchanged. By the assumption that the $\mathsf {LRPC^+}$ problem is hard, this game is indistinguishable from the previous game:

$$\left| \, \Pr [{ \textsf {S}}_2] - \Pr [{ \textsf {S}}_1] \,\right| \le \epsilon _\mathsf {lrpc^+}$$

$\mathbf{Game G }_3$ : We can now reduce the security of the ${\mathsf {IBE}}$ in the previous game to the security of ${\mathsf {RankPKE}}$. We are given the public key ${\varvec{p}}^\star$ of ${\mathsf {RankPKE}}$ and try to break the semantic security of ${\mathsf {RankPKE}}$. Intuitively, we proceed as follows. We will try to embed the given public key ${\varvec{p}}^\star$ of ${\mathsf {RankPKE}}$ to $H(id^\star )$. The ${\mathsf {IBE}}$ for $id^\star$ becomes thus a ${\mathsf {RankPKE}}$ with the same distribution of public keys. We can then use the given challenge ciphertext of ${\mathsf {RankPKE}}$ as the challenge ciphertext to $\mathcal {A}$ and whenever $\mathcal {A}$ can break ${\mathsf {IBE}}$, we can break ${\mathsf {RankPKE}}$. The difficulty in this strategy is that we should correctly guess the challenge identity $id^\star$. In a selective game where $\mathcal {A}$ has to announce $id^\star$ at the beginning of the game, we know this identity. However, in the adaptive game that we consider, we need make a guess on the challenge identity among all the identities queried to H. This explains why we lose a factor $q_H$ in the advantage to attack ${\mathsf {RankPKE}}$.

Now, formally, on input a random matrix ${\varvec{A}}$ and a public key ${\varvec{p}}^\star$ for the ${\mathsf {RankPKE}}$, we choose an index i among $1,\dots q_H$ uniformly at random and change the answer for the ith query to H and for the challenge as follows:

• Hash queries: on $\mathcal {A}$’s jth distinct query $id_j$ to H: if $j = i$, then add the tuple $(id_j,{\varvec{p}}^\star ,\perp )$ to $\mathsf {List}_H$ and return ${\varvec{p}}^\star$ to $\mathcal {A}$. Otherwise for $j\ne i$, do the same as in the previous game.

• Secret key queries: when $\mathcal {A}$ asks for a secret key for the identity id, retrieve the tuple $(id, {\varvec{p}}, {\varvec{s}})$ from the $\mathsf {List}_H$. If ${\varvec{s}}\ne \perp$, return ${\varvec{s}}$ to $\mathcal {A}$, otherwise output a random bit and abort.

• Challenge ciphertext: when $\mathcal {A}$ submits a challenge identity $id^\star$, different from all its secret key queries, and two messages $m_0, m_1$, if $id^\star = id_i$, i.e., $(id^\star , {\varvec{p}}^\star ,\,\perp ) \notin \mathsf {List}_H$, then output a random bit and abort. Otherwise, we also submits the messages $m_0, m_1$ to the challenger and receive a challenge ciphertext $c^\star$. We return then $c^\star$ to $\mathcal {A}$.

When $\mathcal {A}$ terminates and returns a bit b, we also outputs b. We now analyze the advantage to break ${\mathsf {RankPKE}}$:

• We do not abort if we made a good guess, i.e, $id^\star = id_i$. As i is perfectly hidden from $\mathcal {A}$, the probability that we do not abort is $\frac{1}{q_H}$.

• Conditioned on not aborting, the view we provides to $\mathcal {A}$ is exactly the same as in the previous game. We get thus the same advantage in attacking ${\mathsf {RankPKE}}$ as $\mathcal {A}$’s advantage in attacking ${\mathsf {IBE}}$

We finally have:

$$ \mid 2\Pr [{ \textsf {S}}_3] - 1 \mid \le q_H \epsilon _\mathsf {pke}$$

6 Parameters

In this section, we explain how to construct a set of parameters and give an analysis of the best known attacks against the ${\mathsf {IBE}}$ scheme.

6.1 General Parameters for RankSign and RankEnc

First, we have to carefully choose the parameters of the algorithm RankSign [28] used for the presampling phase. In the case where only ${\mathsf {RankPKE}}$ is used, the constraints are much weaker. Remember that RankSign is a probabilistic signature algorithm and the probability of returning a valid signature depends on the choice of the parameters. These parameters are:

• q, m : the cardinality of the base field and the degree of the extension field.

• n : the length of the hidden LRPC code used to sign.

• t : the number of random columns added to the LRPC to hide it.

• k, d : the dimension of the LRPC code and the weight of the LRPC code.

• r : the weight of the signature.

The conditions these parameters must verify are [28]

$$n = d(n-k), (r-t)(m-r)+(n-k)(rd-m)=0,~r = t + \frac{n-k}{d}$$

Let us explain the choice of our parameters. First we need to fix d for two reasons:

• if we look at the three conditions, they are homogeneous if d is constant. Thus, we can make other set of parameters from one set by multiply all the parameters (except for d) by a constant.

• d is the weight of the $LRPC^+$ code used for the public master key. It is very important to choose d not too small to ensure the security of the public master key.

Once d is fixed, we can easily test all the valid parameters and choose the most interesting ones, whether we need to optimize the security or the key size.

Then we need to choose the parameters of ${\mathsf {RankPKE}}$. We need a code which can correct wr errors, where w is the weight of the matrix ${\varvec{U}}$. We use $(n',k',t')$-simple codes because because they can asymptotically decode up to $d_{GV}$ errors. In all cases, we have chosen $n'=m$ for simplicity, even if this is not a necessary condition.

Let us describe the size of the keys and of the messages, as well as the computation time of our cryptosystem:

• public master key ${\varvec{A}}$ is a $(k\,+\,t)\times (n\,+\,t)$ matrix over $\mathbb {F}_{q^m}$: $(k\,+\,t)(n-k)m\left\lceil \log _2 q \right\rceil$ bits (under systematic form).

• public key ${\varvec{p}}_{id}$ is an element of $\mathbb {F}_{q^m}^{n+t}$: $(n+t)m\left\lceil \log _2 q \right\rceil$ bits.

• secrete key ${\varvec{s}}_{id}$ is an element of $\mathbb {F}_{q^m}^{n-k}$: $(n-k)m\left\lceil \log _2 q \right\rceil$ bits.

• plaintext ${\varvec{m}}$ is an element of $\mathbb {F}_{q^m}^{k'}$: $k'm\left\lceil \log _2 q \right\rceil$ bits.

• ciphertext is a $(k+t+1)\times n'$ matrix over $\mathbb {F}_{q^m}$: $(k+t+1)n'm\left\lceil \log _2 q \right\rceil$ bits.

• to generate the secret key, we need to invert a syndrome with ${\mathsf {RankSign}}$ which takes $(n-k)(n+t)$ multiplications in $\mathbb {F}_{q^m}$ [28].

• encryption consists in a multiplication of two matrices of respective sizes $(k+t+1)\times (n+t)$ and $(n+t)\times n'$, which takes $(k+t+1)(n+t)n'$ multiplications in $\mathbb {F}_{q^m}$.

• decryption consists in a multiplication matrix-vector and the decoding of an error of weight wr with a $(n',k',t')$-simple code, which takes $(k+t+1)n'$ multiplications in $\mathbb {F}_{q^m}$ and $\mathcal {O}\big ({((n'-t')wr)^3}\big )$ operations in $\mathbb {F}_q$.

A multiplication in $\mathbb {F}_{q^m}$ costs $\tilde{\mathcal {O}}\big ( m \log q \big )$ operations in $\mathbb {F}_2$ [45].

6.2 Practical Evaluation of the Security

In order to analyze the security of the IBE, we recall the result of the Theorem 4: $\epsilon _\mathsf {ibe}\le \frac{2q_H}{q} + \epsilon _\mathsf {lrpc^+}+ q_H( \epsilon _\mathsf {drsd}+ \epsilon _\mathsf {pke})$. We want $\epsilon _\mathsf {ibe}\leqslant 2^{-\lambda }$, where $\lambda$ is the security parameter. Since the first term only depends on q and on the number of queries, we need $q > q_H 2^{\lambda +1}$. We stress that the size of the data and the computation time are linear in the logarithm of q. In consequence, it is not a problem to have q exponential in the security parameter. Moreover, since all combinatorial attacks are polynomial in q, they are utterly inefficient to break the IBE.

The second type of attacks are the algebraic attacks. An adversary can either attack the public master key ${\varvec{A}}$ by solving an instance of $\mathsf {LRPC^+}$ problem, a public key ${\varvec{p}}$ of an user by solving an instance of $\mathsf {DRSD}$ or a ciphertext by solving an instance of $\mathsf {RSL}$. By using the results in [6], we can estimate the complexity of the attacks and adapt the parameters in consequence.

We give an example of a set of parameters in the following table. We take the standard values $\lambda = 128$ for the security parameter and $q_H = 2^{60}$.

n	$n-k$	m	q	d	t	r	$d_{GV}$	$d_{Sing}$	Public master key Size (Bytes)	$n'$	$k'$	$t'$	w	Probability of failure
100	20	96	$2^{192}$	5	12	16	11	20	4,239,360	96	9	66	4	$2^{-576}$

The decoding algorithm for the simple codes is probabilistic, that is why there is a probability $p_f$ that the decoding fails. However, $p_f \approx \frac{1}{q^{t'-wr+1}}$, since we have a very large q in this example, $p_f$ is negligible. These parameters are large but still tractable, for a first code-based ${\mathsf {IBE}}$ scheme in post-quantum cryptography.