Human Mobility, Networks and Disease Dynamics on a Global Scale

Abstract

Disease dynamics is a complex phenomenon and in order to address these questions expertises from many disciplines need to be integrated. One method that has become particularly important during the past few years is the development of computational models and computer simulations that help addressing these questions. In the focus of this chapter are emergent infectious diseases that bear the potential of spreading across the globe, exemplifying how connectivity in a globalized world has changed the way human-mediated processes evolve in the 21st century. The examples of most successful predictions of disease dynamics given in the chapter illustrate that just feeding better and faster computers with more and more data may not necessarily help understanding the relevant phenomena. It might rather be much more useful to change the conventional way of looking at the patterns and to assume a correspondingly modified viewpoint—as most impressively shown with the examples given in this chapter.

1 Introduction

In early 2009, news accumulated in major media outlets about a novel strain of influenza circulating in major cities in Mexico [1]. This novel H1N1 strain was quickly termed “swine flu”, in reference to its alleged origin in pig populations before jumping the species border to humans. Very quickly public health institutions were alerted and saw the risk of this local influenza epidemic becoming a major public health problem globally. The concerns were serious because this influenza strain was of the H1N1 subtype, the same virus family that caused one of the biggest pandemics in history, the Spanish flu that killed up to 40 million people in the beginning of the 20th century [2]. The swine flu epidemic did indeed develop into a pandemic, spreading across the globe in matters of months. Luckily, the strain turned out to be comparatively mild in terms of symptoms and as a health hazard. Nevertheless, the concept of emergent infectious diseases, novel diseases that may have dramatic public health, societal and economic consequences reached a new level of public awareness. Even Hollywood picked up the topic in a number of blockbuster movies in the following years [3]. Only a few years later, MERS hit the news, the Middle East Respiratory Syndrome, a new type of virus that infected people in the Middle East [4]. MERS was caused by a new species of corona virus of the same family of viruses that the 2003 SARS virus belonged to. And finally, the 2013 Ebola crisis in West African countries Liberia, Sierra Leone and Guinea that although it did not develop into a global crisis killed more than 10000 people in West Africa [5].

Emergent infectious diseases have always been part of human societies, and also animal populations for that matter [6]. Humanity, however, underwent major changes along many dimensions during the last century. The world population has increased from approx. 1.6 billion in 1900 to 7.5 billion in 2016 [7]. The majority of people now live in so-called mega-cities, large scale urban conglomerations of more than 10 million inhabitants that live in high population densities [8] often in close contact with animals, pigs and fowl in particular, especially in Asia. These conditions amplify not only the transmission of novel pathogens from animal populations to human, high frequency human-to-human contacts yield a potential for rapid outbreaks of new pathogens.

Fig. 19.1

The global air-transportation network. Each node represents one of approx. 4000 airports, each link one of approx. 50000 direct connections between airports. More than 3 billion passengers travel on this network each year. All in all every day more than 16 billion km are traversed on this network, three times the radius of our solar system

Population density is only one side of the coin. In addition to increasing face-to-face contacts within populations we also witness a change of global connectivity [9]. Most large cities are connected by means of an intricate, multi-scale web of transportation links, see Fig. 19.1. On a global scale worldwide air-transportation dominates this connectivity. Approx. 4,000 airports and 50,000 direct connections span the globe. More than three billion passengers travel on this network each year. Every day the passengers that travel this network accumulate a total of more than 14 billion kilometers, which is three times the radius of our solar system [10, 11]. Clearly this amount of global traffic shapes the way emergent infectious diseases can spread across the globe. One of the key challenges in epidemiology is preparing for eventual outbreaks and designing effective control measures. Evidence based control measures, however, require a good understanding of the fundamental features and characteristics of spreading behavior that all emergent infectious diseases share. In this context this means addressing questions such as: If there is an outbreak at location X when should one expect the first case at a distant location Y? How many cases should one expect there? Given a local outbreak, what is the risk that a case will be imported in some distant country. How does this risk change over time? Also, emergent infectious diseases often spread in a covert fashion during the onset of an epidemic. Only after a certain number of cases are reported, public health scientists, epidemiologist and other professionals are confronted with cases that are scattered across a map and it is difficult to determine the actual outbreak origin. Therefore, a key question is also: Where is the geographic epicenter of an ongoing epidemic?

Disease dynamics is a complex phenomenon and in order to address these questions expertises from many disciplines need to be integrated, such as epidemiolgy, spatial statistics, mobility and medical research in this context. One method that has become particularly important during the past few years is the development of computational models and computer simulations that help address these questions. These are often derived and developed using techniques from theoretical physics and more recently complex network science.

2 Modeling Disease Dynamics

Modeling the dynamics of diseases using methods from mathematics and dynamical systems theory has a long history. In 1927 Kermack and McKenrick [12] introduced and analyzed the “Suceptible-Infected-Recovered” (SIR) model, a parsimoneous model for the description of a large class of infectious diseases that is also still in use today [13]. The SIR model considers a host population in which individuals can be susceptible (S), infectious (I) or recovered (R). Susceptible individuals can aquire a disease and become infectious themselves and transmit the disease to other susceptible individuals. After an infectious period individuals recover, acquire immunity, and no longer infect others. The SIR model is an abstract model that reduces a real world situation to the basic dynamic ingredients that are believed to shape the time course of a typical epidemic. Structurally, the SIR model treats individuals in a population in much the same way as chemicals that react in a well-mixed container. Chemical reactions between reactants occur at rates that depend on what chemicals are involved. It is assumed that all individuals can be represented only by their infectious state and are otherwise identical. Each pair of individuals has the same likelihood of interacting. Schematically, the SIR model is described by the following reactions

$$\begin{aligned} S+I\xrightarrow {\alpha }2I\qquad I\xrightarrow {\beta }R \end{aligned}$$

(19.1)

where $\alpha$ and $\beta$ are transmission and recovery rates per individual, respectively. The expected duration of being infected, the infectious period is given by $T=\beta ^{-1}$ which can range from a few days to a few weeks for generic diseases. The ratio of rates $R_{0}=\alpha /\beta$ is known as the basic reproduction ratio, i.e. the expected number of secondary infections caused by a single infected individual in a fully susceptible population. $R_{0}$ is the most important epidemiological parameter because the value of $R_{0}$ determines whether an infectious disease has the potential for causing an epidemic or not. When $R_{0}>1$ a small fraction of infected individuals in a susceptible population will cause an exponential growth of the number of infections. This epidemic rise will continue until the supply of susceptibles decreases to a level at which the epidemic can no longer be sustained. The increase in recovered and thus immune individuals dilutes the population and the epidemic dies out. Mathematically, one can translate the reaction scheme (19.1) into a set of ordinary differential equations. Say the population has $N\gg 1$ individuals. For a small time interval $\Delta t$ and a chosen susceptible individual the probability of that individual interacting with an infected is proportional to the fraction I / N of infected individuals. Because we have S susceptibles the expected change of the number susceptibles due to infection is

$$\begin{aligned} \Delta S\approx -\Delta t\times \alpha \times S\times \frac{I}{N} \end{aligned}$$

(19.2)

where the rate $\alpha$ is the same as in (19.1) and the negative sign accounts for the fact that the number of susceptibles decreases. Likewise the number of infected individuals is increased by the same amount $\Delta I=+\Delta t\times \alpha \times S\times I/N.$ The number of infecteds can also decrease due to the second reaction in (19.1). Because each infected can spontaneouly recover the expected change due to recovery is

$$\begin{aligned} \Delta I\approx -\Delta t\times \beta \times I. \end{aligned}$$

(19.3)

Based on these assumptions Eqs. (19.2) and (19.3) become a set of differential equations that describe the dynamics of the SIR model in the limit $\Delta t\rightarrow 0$:

$$\begin{aligned} ds/dt= & {} -\alpha sj\\ dj/dt= & {} \alpha sj-\beta j\nonumber \\ r= & {} 1-s-j\nonumber \end{aligned}$$

(19.4)

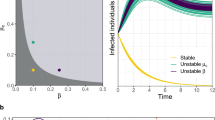
where $s(t)=S(t)/N$, $j(t)=I(t)/N$ and $r(t)=R(t)/N$ are the fractions of susceptibles, infecteds and recovereds in the population as a function of time. The last equation in (19.4) is a consequence of the conservation of individuals, $S(t)+I(t)+R(t)=N$. Solutions to this set of equations for a small initial fraction of infecteds $j(0)=j_{0}$, $r(0)=0$, and $s(0)=1-j_{0}$ exhibit a typical epi-curve, i.e. an initial exponential increase of infecteds with a subsequent decline if the basic reproduction ratio $R_{0}>1$. Typical solutions of the SIR model are shown in Fig. 19.2. A more realistic approach accounts for fluctuations that are caused by the intrinsic randomness of the probabilistic reactions (19.1) and the finite number N of individuals in a population. Depending on the magnitude of N a model in which reactions occur randomly at rates $\alpha$ and $\beta$ a stochastic system generally exhibits solutions that fluctuate around the solutions to the deterministic system of Eq. (19.4).

Fig. 19.2

The SIR model. The curves depict the generic time course of the fraction of infected individuals j(t) generated by the SIR model defined by reactions (19.1, colored trajectories) and Eq. (19.4, black line). Initially only a small fraction of $1\%$ of the population is infected. When $R_{0}>1$ (here $R_{0}=2.5$ and $\beta ^{-1}=1\,\text {week}$) an exponential growth is followed by an exponential decay, leading to the generic epidemic curve. The fluctuations in the colored trajectories are generated by a stochastic generalization of the deterministic system defined by Eq. (19.4) in which in a finite population of $N=1000$ individuals transmission and recovery events (reactions (19.1)) occur randomly

Both, the deterministic SIR model and the more general particle kinetic stochastic model are designed to model disease dynamics in a single population, spatial dynamics or movement patterns of the host population are not accounted for. These systems are thus known as well-mixed systems in which the analogy is one of chemical reactants that are well-stirred in a chemical reaction container as mentioned above.

2.1 Spatial Models

When a spatial component is expected to be important in natural scenario, several methodological approaches exist to account for space. Essentially the inclusion of a spatial component is required when the host is mobile and can transport the state of infection from one location to another. The combination of local proliferation of an infection and the disperal of infected host individuals then yields a spread along the spatial dimension [13, 14].

One of the most basic ways of incorporating a spatial dimension and host dispersal is by assuming that all quantities in the SIR model are also functions of a location $\mathbf {x}$, so the state of the system is defined by $s(\mathbf {x},t)$, $j(\mathbf {x},t)$ and $r(\mathbf {x},t)$. Most frequently two spatial dimensions are considered. The simplest way of incorporating dispersal is by an ansatz following Eq. (2.19) in Chap. 2 which assumes that individuals move diffusively in space which yields the reaction-diffusion dynamical system

$$\begin{aligned} \partial s/\partial _{t}= & {} -\alpha js+D\nabla ^{2}s\end{aligned}$$

(19.5)

$$\begin{aligned} \partial j/\partial _{t}= & {} \alpha js-\beta j+D\nabla ^{2}j\end{aligned}$$

(19.6)

$$\begin{aligned} \partial r/\partial _{t}= & {} \beta j+D\nabla ^{2}r \end{aligned}$$

(19.7)

where e.g. in a two-dimensional system with $\mathbf {x}=(x,y)$ the Laplacian is $\nabla ^{2}=\partial ^{2}/\partial _{x}^{2}+\partial ^{2}/\partial _{y}^{2}$ and the parameter D is the diffusion coefficient. The reasoning behind this approach is that the net flux of individuals of one type from one location to a neighboring location is proportional to the gradient or the difference in concentration of that type of individuals between neighboring locations. The key feature of diffusive dispersal is that it is local, in a discretized version the Laplacian permits movements only within a limited distance.

In reaction diffusion systems of this type the combination of initial exponential growth (if $R_{0}=\alpha /\beta >1$) and diffusion ($D>0$) yields the emergence of an epidemic wavefront that progresses at a constant speed if initially the system is seeded with a small patch of infected individuals [15]. The advantage of parsimoneous models like the one defined by Eq. (19.7) is that properties of the emergent epidemic wavefront can be computed analytically, e.g. the speed of the wave in the above system is related to the basic reproduction number and diffusion coefficient by

$$\begin{aligned} v\sim \sqrt{\left( R_{0}-1\right) D} \end{aligned}$$

(19.8)

in which we recognize the relation of Eq. (2.17). Another class of models considers the reaction of Eq. (19.1) to occur on two-dimensional (mostly square) lattices. In these models each lattice site is in one of the states S, I or R and reactions occur only with nearest neighbors on the lattice. These models account for stochasticity and spatial extent. Given a state of the system, defined by the state of each lattice site, and a small time interval $\Delta t$, infected sites can transmit the disease to neighboring sites that are susceptible with a probability rate $\alpha$. Infected sites also recover to the R state and become immune with probability $\beta \Delta t$. Figure 19.3a illustrates the time course of the lattice-SIR model. Seeded with a localized patch of infected sites, the system exhibits an asymptotic concentric wave front that progresses at an overall constant speed if the ratio of transmission and recovery rate is sufficiently large. Without the stochastic effects that yield the irregular interface at the infection front, this system exhibits similar properties to the reaction diffusion system of Eq. (19.7). In both systems transmission of the disease in space is spatially restricted per unit time.

Fig. 19.3

Stochastic lattice SIR models. a From left to right the images are temporal snapshots of a stochastic SIR model in which an infected lattice site (red) can transmit an infection to a susceptible (white) neighboring site with probability rate $\alpha$. At rate $\beta$ infected sites recover and become immune (grey). Initially a single site in the center is infected. Asmyptotically a concentric pattern emerges. The infection front spreads at a constant speed. Stochastic effects at the wavefront caused the ragged structure of the interface. b The system is identical to the system depicted in (a). However, in addition to the generic next neighbor transmission, with a small but significant probability a transmission to a distant site can occur. This probability also decreases with distance as an inverse power-law, e.g. $p(d)\sim d^{-(1+\mu )}$ where the exponent is in the range $0<\mu <2$. Because the rare but significant occurance of long-range transmissions, a more complex pattern emerges, the concentric nature observed in system a is gone. Instead, a fractal, multiscale pattern emerges

2.2 The Impact of Long-Distance Transmissions

The stochastic lattice model is particularly useful for investigating the impact of permitting long-distance transmissions. Figure 19.3b depicts temporal snapshots of a simulation that is identical to the system of Fig. 19.3a apart from a small but significant difference. In addition for infected sites to transmit the disease to neighboring susceptible lattice sites, every now and then (with a probability of $1\%$) they can also infect randomly chosen lattice sites anywhere in the system. The propensity of infecting a lattice site at distance r decreases as an inverse power-law as explained in the caption to Fig. 19.3. The possibility of transmitting to distant locations yields new epidemic seeds far away that subsequently turn into new outbreak waves and that in turn seed second, third, etc. generation outbreaks, even if the overall rate at which long-distance transmission occur is very small. The consequence of this is that the spatially coherent, concerntric pattern observed in the reaction diffusion system is lost, and a complex spatially incoherent, fractal pattern emerges [16,17,18]. Practically, this implies that the distance from an initial outbreak location can no longer be used as a measure for estimating or computing the time that it takes for an epidemic to arrive at a certain location. Also, given a snapshot of a spreading pattern, it is much more difficult to reconstruct the outbreak location from the geometry of the pattern alone, unlike in the concentric system where the outbreak location is typically near the center of mass of the pattern.

Fig. 19.4

Arrival time and geographic distance. Each panel depicts the relation of epidemic arrival time and geographic distance to the initial outbreak location (country of origin) for two different recent epidemics, the H1N1 pandemic 2009 (left) and the SARS epidemic 2003 (right). Because of the complexity of connectivity of the worldwide air-transportation network (see Fig. 19.1) geographic distance to the initial outbreak location is no longer a good predictor of arrival time, unlike in systems with local or spatially limited host mobility

A visual inspection of the air-transportation system depicted in Fig. 19.1 is sufficiently convincing that the significant fraction of long-range connections in global mobility will not only increase the speed at which infectious diseases spread but, more importantly, also cause the patterns of spread to exhibit high spatial incoherence and complexity caused by the intricate connectivity of the air-transportation network. As a consequence we can no longer use geographic distance to an emergent epidemic epicenter as an indicator or measure of “how far away” that epicenter is and how long it will take to travel to a given location on the globe. This type of decorrelation is shown in Fig. 19.4 for two examples: The 2003 SARS epidemic and the 2009 influenza H1N1 pandemic. On a spatial resolution of countries, the figure depicts scatter plots of the epidemic arrival time as a function of geodesic (shortest distance on the surface of the Earth) distance from the initial outbreak location. As expected, the correlation between distance and arrival time is weak.

3 Modeling Disease Dynamics on a Global Scale

Given that models based on local or spatially limited mobility are inadequate, improved models must be developed that account for both, the strong heterogeneity in population density, e.g. that human populations accumulate in cities that vary substantially in size, and the connectivity structure between them that is provided by data on air traffic. In a sense one needs to establish a model that captures that the entire population is a so-called meta-population, a system of $m=1,\ldots ,M$ subpopulation, each of size $N_{m}$ and traffic between them, e.g. specifying a matrix $F_{nm}$ that quantifies the amount of host individuals that travel from population m to population n in a given unit of time [19, 20]. For example $N_{n}$ could correspond to the size of city n and $F_{nm}$ the amount of passengers the travel by air from m to n. One of earliest and most employed models for disease dynamics using the meta-population approach is a generalization of Eq. (19.4) in which each population’s dynamics is governed by the ordinary SIR model, e.g.

$$\begin{aligned} dS_{n}/dt= & {} -\alpha S_{n}I_{n}/N_{n}\\ dI_{n}/dt= & {} \alpha S_{n}I_{n}/N_{n}-\beta I_{n}\nonumber \\ dR_{n}/dt= & {} \beta I_{n}\nonumber \end{aligned}$$

(19.9)

where the size $N_{n}=R_{n}+I_{n}+S_{n}$ of population n is a parameter. In addition to this, the exchange of individuals between populations is modeled in such a way that hosts of each class move from location m to location n with a probability rate $\omega _{nm}$ which yields

$$\begin{aligned} dU_{n}/dt=\sum _{m}\left( \omega _{nm}U_{m}-\omega _{mn}U_{n}\right) \end{aligned}$$

(19.10)

where $U_{m}$ is a placeholder for $S_{m}$, $I_{m}$ and $R_{m}.$ The first term corresponds to the flux into location n from all other locations, the second term the flux in the opposite direction. Combining Eqs. (19.9) and (19.10) yields:

$$\begin{aligned} dS_{n}/dt= & {} -\alpha S_{n}I_{n}/N_{n}+\sum _{m}\left( \omega _{nm}S_{m}-\omega _{mn}S_{n}\right) \\ dI_{n}/dt= & {} \alpha S_{n}I_{n}/N_{n}-\beta I_{n}+\sum _{m}\left( \omega _{nm}I_{m}-\omega _{mn}I_{n}\right) \nonumber \\ dR_{n}/dt= & {} \beta I_{n}+\sum _{m}\left( \omega _{nm}R_{m}-\omega _{mn}R_{n}.\right) \nonumber \end{aligned}$$

(19.11)

which is a generic metapopulation SIR model. In principle one is required to fix the infection-related parameters $\alpha$ and $\beta$ and the population sizes $N_{m}$ as well as the mobility rates $\omega _{nm}$, i.e. the number of transitions from m to n per unit time. However, based on very plausible assumptions [11], the system can be simplified in such a way that all parameters can be gauged against data that is readily available, e.g. the actual passenger flux $F_{nm}$ (the amount of passengers that travel from m to n per day) that defines the air-transportation network, without having to specify the absolute population sizes $N_{n}$.

First the general rates $\omega _{nm}$ have to fulfill the condition

$$ \omega _{nm}N_{m}=\omega _{mn}N_{n} $$

if we assume that the $N_{n}$ remain constant. If we assume, additionally, that the total air traffic flowing out of a population n obeys

$$ F_{n}=\sum _{m}F_{mn}\sim N_{n}, $$

i.e. it is proportional to the size of the population (e.g. the supply is proportional to the demand), the model defined by Eq. (19.11) can be recast into

$$\begin{aligned} ds_{n}/dt= & {} -\alpha s_{n}\,j_{n}+\gamma \sum _{m}P_{mn}\left( s_{m}-s_{n}\right) \\ dj_{n}/dt= & {} \alpha s_{n}j_{n}-\beta j_{n}+\gamma \sum _{m}P_{mn}\left( j_{m}-j_{n}\right) \nonumber \\ r_{n}= & {} 1-s_{n}-j_{n}.\nonumber \end{aligned}$$

(19.12)

where the dynamic variables are, again, fractions of the population in each class: $s_{n}=S_{n}/N_{n}$, $j_{n}=I_{n}/N_{n}$, and $r_{n}=R_{n}/N_{n}$. In this system the new matrix $P_{mn}$ and the new rate parameter $\gamma$ can be directly computed from the traffic matrix $F_{nm}$ and the total population involved $\mathscr {N}=\sum _{m}N_{m}$ according to

$$ P_{nm}=\frac{F_{nm}}{\sum _{k}F_{km}} $$

and

$$ \gamma =\mathscr {F}/\mathscr {N} $$

where $\mathscr {F}=\sum _{n,m}F_{mn}$ is the total traffic in the network. The matrix $P_{nm}$ is therefore the fraction of passengers that are leaving node m with destination n. Because passengers must arrive somewhere we have $\sum _{n}P_{nm}=1$.

An important first question is concerning the different time scales, i.e. the parameters $\alpha$, $\beta$ and $\gamma$ that appear in system (19.12). The inverse $\beta ^{-1}=T$ is the infectious period, that is the time individuals remain infectious. If we assume $T\approx 4$–6 days and $R_{0}=\alpha /\beta \approx 2$ both rates are of the same order of magnitude. How about $\gamma$? The total number of passengers $\mathscr {F}$ is approximately $8\times 10^{6}$ per day. If we assume that $\mathscr {N}\approx 7\times 10^{9}$ people we find that

$$ \gamma \approx 0.0015\,\text {d}^{-1}. $$

It is instructive to consider the inverse $T_{\text {travel}}=\gamma ^{-1}\approx 800$ days. On average a typical person boards a plane every 2–3 years or so. Keep in mind though that this is an average that accounts for both a small fraction of the population with a high frequency of flying and a large fraction that almost never boards a plane. The overall mobility rate $\gamma$ is thus a few orders of magnitude smaller than those rates related to transmissions and recoveries. This has important consequences for being able to replace the full dynamic model by a simpler model discussed below.

Figure 19.5 depicts a numerical solution to the model defined by Eq. (19.12) for a set of initial outbreak locations. At each location a small seed of infected individuals initializes the epidemic. Global aspects of an epidemic can be assessed by the total fraction of infected individuals $j_{G}(t)=\sum _{n}c_{n}j_{n}(t)$ where $c_{n}$ is the relative size population n with respect to the entire population size $\mathscr {N}$. As expected the time course of a global epidemic in terms of the epicurve and duration depends substantially on the initial outbreak location.

Fig. 19.5

Global epi-curves. Each curve depicts the global fraction of infected individuals as a function of time for different outbreak locations as predicted by the metapopulation model defined by Eq. (19.12). Depending on the initial outbreak location curves differ in epidemic maximum, curve shape and epidemic duration

Fig. 19.6

Properties of spatiotemporal patterns of global disease dynamics. Each panel from left to right depicts temporal snapshots of the spread of a computer-simulated hypothetical pandemic. Red nodes denote locations with a high fraction of infecteds. Each row corresponds to a different initial outbreak location (London (LHR), top and Chicago (ORD), bottom). The patterns are spatially incoherent, especially for larger times. It is thus difficult to assess which locations are affected next in the sequence of locations

Fig. 19.7

Arrival time and geographic distance. For a simulated pandemic based on the dynamical system of Eq. (19.12) and the worldwide air-transportation network (top) the bottom panel depicts the arrival time at each location as a function of the geographic distance to the initial outbreak location Hong Kong. Airports are colored according to geographic location. Only a weak correlation between arrival time and geographic distance exists (dashed line). For a fixed small range of geographic distances a wide range of arrival times exists, geographic distance is thus not a good predictor

A more important aspect is the spatiotemporal pattern generated by the model. Figure 19.6 depicts temporal snapshots of simulations initialized in London and Chicago, respectively. Analogous to the qualitative patterns observed in Fig. 19.3b, we see that the presence of long-range connections in the worldwide air-transportation network yields incoherent spatial patterns much unlike the regular, concentric wavefronts observed in systems without long-range mobility. Figure 19.7 shows that also the model epidemic depicts only a weak correlation between geographic distance to the outbreak location and arrival time. For a fixed geographic distance arrival times at different airports can vary substantially and thus the traditional geographic distance is useless as a predictor.

4 Issues with Computational Models

The system defined by Eq. (19.12) is one of the most parsimoneous models that accounts for strongly heterogeneous population distributions that are coupled by traffic flux between them and that can be gauged against actual population size distributions and traffic data. Surprisingly, despite its structural simplicity this type of model has been quite successful in accounting for actual spatial spreads of past epi- and pandemics [19]. Based on early models of this type and aided by the exponential increase of computational power, very sophisticated models have been developed that account for factors that are ignored by the deterministic metapopulation SIR model. In the most sophisticated approaches, e.g. GLEAM [21], the global epidemic and mobility computational tool, not only traffic by air but other means of transportation are considered, more complex infectious dynamics is considered and in hybrid dynamical systems stochastic effects caused by random reactions and mobility events are taken into account. Household structure, available hospital beds, seasonality have been incorporated as well as disease specific features, all in order to make predictions more and more precise. The philosophy of this type of research line heavily relies on the increasing advancement of both computational power as well as more accurate and pervasive data often collected in natural experiments and webbased techniques [21,22,23,24,25].

Despite the success of these quantitative approaches, this strategy bears a number of problems some of which are fundamental. First, with increasing computational methods it has become possible to implement extremely complex dynamical systems with decreasing effort and also without substantial knowledge of the dynamical properties that often nonlinear dynamical systems can possess. Implementing a lot of dynamical detail, it is difficult to identify which factors are essential for an observed phenomenon and which factors are marginal. Because of the complexity that is often incorporated even at the beginning of the design of a sophisticated model in combination with the lack of data modelers often have to make assumptions about the numerical values of parameters that are required for running a computer simulation [26]. Generically many dozens of unknown parameters exist for which plausible and often not evidence-based values have to be assumed. Because complex computational models, especially those that account for stochasticity, have to be run multiple times in order to make statistical assessments, systematic parameter scans are impossible even with the most sophisticated supercomputers.

Finally, all dynamical models, irrespective of their complexity, require two ingredients to be numerically integrated: (1) fixed values for parameters and (2) initial conditions. Although some computational models have been quite successful in describing and reproducing the spreading behavior of past epidemics and in situations where disease specific parameters and outbreak locations have been assessed, they are difficult to apply in situations when novel pathogens emerge. In these situations, when computational models from a practical point of view are needed most, little is known about these parameters and running even the most sophisticated models “in the dark” is problematic. The same is true for fixing the right initial conditions. In many cases, an emergent infectious disease initially spreads unnoticed and the public becomes aware of a new event after numerous cases occur in clusters at different locations. Reconstructing the correct initial condition often takes time, more time than is usually available for making accurate and valueable predictions that can be used by public health workers and policy makers to devise containment strategies.

5 Effective Distance

Given the issues discussed above one can ask if alternative approaches exist that can inform about the spread without having to rely on the most sophisticated highly detailed computer models. In this context one may ask whether the complexity of the observed patterns that are solutions to models like the SIR metapopulation model of Eq. (19.12) are genuinely complex because of the underlying complexity of the mobility network that intricately spans the globe, or whether a simple pattern is really underlying the dynamics that is masked by this complexity and our traditional ways of using conventional maps for displaying dynamical features and our traditional ways of thinking in terms of geographic distances.

In a recent approach Brockmann and Helbing [11] developed the idea of replacing the traditional geographic distance by the notion of an effective distance derived from the topological structure of the global air-transportation network. In essence the idea is very simple: If two locations in the air-transportation network exchange a large number of passengers they should be effectively close because a larger number of passengers implies that the probability of an infectious disease to be transmitted from A to B is comparatively larger than if these two locations were coupled only by a small number of traveling passengers. Effective distance should therefore decrease with traffic flux. What is the appropriate mathematical relation and a plausible ansatz to relate traffic flux to effective distance? To answer this question one can go back to the metapopulation SIR model, i.e. Eq. (19.12). Dispersal in this equation is governed by the flux fraction $P_{nm}$. Recall that this quantity is the fraction of all passengers that leave node m and arrive at node n. Therefore $P_{nm}$ can be operationally defined as the probability of a randomly chosen passenger departing node m arriving at node n. If, in a thought experiment, we assume that the randomly selected person is infectious, $P_{nm}$ is proportional to the probability of transmitting a disease from airport m to airport n. We can now make the following ansatz for the effective distance:

$$\begin{aligned} d_{nm}=d_{0}-\log P_{nm} \end{aligned}$$

(19.13)

where $d_{0}\ge 0$ is a non-negative constant to be specified later. This definition of effective distance implies that if all traffic from m arrives at n and thus $P_{nm}=1$ the effective distance is $d_{nm}=d_{0}$ which is the smallest possible value. If, on the other hand $P_{nm}$ becomes very small, $d_{nm}$ becomes larger as required. The definition (19.13) applies to nodes m and n that are connected by a link in the network. What about pairs of nodes that are not directly connected but only by paths that require intermediate steps? Given two arbitrary nodes, an origin m and a destination n, an infinite amount of paths (sequence of steps) exist that connect the two nodes. We can define the shortest effective route as the one for which the accumulation of effective distances along the legs is minimal. So for any path we sum the effective distance along the legs according to Eq. (19.13) adding up to an effective distance $D_{nm}$. This approach also explains the use of the logarithm in the definition of effective distance. Adding effective distances along a route implies the multiplication of the probabilities $P_{nm}$ along the involved steps. Therefore the shortest effective distance $D_{nm}$ is equivalent to the most probable path that connect origin and destination. The parameter $d_{0}$ is a free parameter in the definition and quantifies the influence of the number of steps involved in a path. Typically it is chosen to be either 0 or 1 depending on the application.

One important property of effective distance is its asymetry. Generally we have

$$ d_{nm}\ne d_{mn}. $$

This may seem surprising at first sight, yet it is plausible. Consider for example two airports A and B. Let’s assume A is a large hub that is strongly connected to many other airports in the network, including B. Airport B, however, is only a small airport with only as a single connection leading to A. The effective distance $B\rightarrow A$ is much smaller (equal to $d_{0}$) than the effective distance from the hub A to the small airport B. This accounts for the fact that if, again in a thought experiment, a randomly chosen passenger at airport B is most definitely going to A whereas a randomly chosen passenger at the hub A is arriving at B only with a small probability.

Given the definition of effective distance one can compute the shortest effective paths to every other node from a chosen and fixed reference location. Each airport m thus has a set of shortest paths $\mathscr {P}_{m}$ that connect m to all other airports. This set forms the shortest path tree $T_{m}$ of airport m. Together with the effective distance matrix $D_{nm}$ the tree defines the perspective of node m. This is illustrated qualitatively in the Fig. 19.8 that depicts a planar random triangular weighted network.

Fig. 19.8

Shortest paths and shortest path trees in complex networks. Left: A random planar weighted network consisting of 100 nodes and 283 links. Links vary in strength. The size of the nodes quantifies the total link weight per node. Center: For a chosen node (no. 76) the shortest path tree is shown. Color depicts effective distance. Right: The shortest path tree of node no. 36. The shortest path trees are also those paths that correspond to the most probable paths of a random walker that starts at the reference location and terminates at the respective target node

One can now employ these principles and compute the shortest path trees and effective distances from the perspective of actual airports in the worldwide air-transportation network based on actual traffic data, i.e. the flux matrix $F_{nm}$. Figure 19.9 depicts the shortest path tree of one of the Berlin airports (Tegel, TXL). The radial distance of all the other airports in the network is proportional to their effective distance from TXL. One can see that large European hubs are effectively close to TXL as expected. However, also large Asian and American airports are effectively close to TXL. For example the airports of Chicago (ORD), Beijing (PEK), Miami (MIA) and New York (JFK) are comparatively close to TXL. We can also see that from the perspective of TXL, Germany’s largest airport FRA serves as a gateway to a considerable fraction of the rest of the world. Because the shortest path tree also represents the most probable spreading routes one can use this method to identify airports that are particularly important in terms of distributing an infectious disease throughout the network.

Fig. 19.9

Shortest path trees and effective distance from the perspective of airport Tegel (TXL) in Berlin. TXL is the central node. Radial distance in the tree quantifies the effective distance to the reference node TXL. As expected large European hubs like Frankfurt (FRA), Munich (MUC) and London Heathrow (LHR) are effective close to TXL. However, also hubs that are geographically distant such as Chicago (ORD) and Beijing (PEK) are effectively closer than smaller European airports. Note also that the tree structure indicates that FRA is a gateway to a large fraction of other airports as reflected by the size of the tree branch at FRA. The illustration is a screenshot of an interactive effective distance tool available online [27]

6 Recovery of Concentric Patterns

The use of effective distance and representing the air-transportation network from the perspective of chosen reference nodes and making use of the more plausible notion of distance that better reflects how strongly different locations are coupled in a networked system is helpful for “looking at” the world. Yet, this representation is more than a mere intuitive and plausible spatial representation. What are the dynamic consequences of effective distance? The true advantage of effective distance is illustrated in Fig. 19.10. This figure depicts the identical computer-simulated hypothetical pandemic diseases as Fig. 19.6. Unlike the latter, that is based on the traditional geographic representation, Fig. 19.10 employs the effective distance and shortest path tree representation from the perspective of the outbreak location as discussed above. Using this method, the spatially incoherent patterns in the traditional representation are transformed into concentric spreading patterns, similar to those expected for simple reaction diffusion systems.

This shows that the complexity of observed spreading patterns is actually equivalent to simple spreading patterns that are just convoluted and masked by the underlying network’s complexity. This has important consequences. Because only the topological features of the network are used for computing the effective distance and no dynamic features are required, the concentricy of the emergent patterns are a generic feature and independent of dynamical properties of the underlying model. It also means that in effective distance, contagion processes spread at a constant speed, and just like in the simple reaction diffusion model one can much better predict the arrival time of an epidemic wavefront, knowing the speed and effective distance. For example if shortly after an epidemic outbreak the spreading commences and the initial spreading speed is assessed, one can forecast arrival times without having to run computationally expensive simulations. Even if the spreading speed is unknown, the effective distance which is independent of dynamics can inform about the sequence of arrival times, or relative arrival times.

Fig. 19.10

Simulations and effective distance. The panels depict the same temporal snapshots of computer simulated hypothetical pandemic scenarios as in Fig. 19.6. The top row corresponds to a pandemic initially seeded at LHR (London) the bottom row at ORD (Chicago). The networks depict the shortest path tree effective distance representation of the corresponding seed airports as in Fig. 19.9. The simulated pandemics that exhibit spatially incoherent complex patterns in the traditional representation (Fig. 19.6) are equivalent to concentric wave fronts that progress at constant speeds in effective distance space. This method thus substantially simplifies the complexity seen in conventional approaches and improves quantitative predictions

The benefit of the effective distance approach can also be seen in Fig. 19.11 in which arrival times of the 2003 SARS epidemic and the 2009 H1N1 pandemic in affected countries are shown as a function of effective distance to the outbreak origin. Comparing this figure to Fig. 19.7 we see that effective distance is a much better predictor of arrival time, a clear linear relationship exists between effective distance and epidemic arrival. Thus, effective distance is a promising tool and concept for application in realistic scenarios, being able to provide a first quantitative assessment of an epidemic outbreak and its potential consequences on a global scale.

Fig. 19.11

Correlation of arrival time with effective distance. Left: the relationship of epidemic arrival time and effective distance for the H1N1 pandemic 2009. Compared to the conventional use of geographic distance effective distance is a much better predictor of epidemic arrival time as is reflected by the linear relationship between arrival time and effective distance, e.g. compare to Fig. 19.7. Right: The same analysis for the 2003 SARS epidemic. Also in this case effective distance is much more strongly correlated with arrival time than geographic distance

7 Reconstruction of Outbreaks

In a number of situation epidemiologists are confronted with the task of reconstructing the outbreak origin of an epidemic. When a novel pathogen emerges in some cases the infection spreads covertly until a substantial case count attracts attention and public health officials and experts become aware of the situation. Quite often cases occur much like the patterns depicted in Fig. 19.3b in a spatially incoherent way because of the complexity of underlying human mobility networks. When cases emerge at apparently randomly distributed locations it is a difficult task to assess where the event initially started. The computational method based on effective distance can also be employed in these situations provided that one knows the underlying mobility network. This is because the concentric pattern depicted in Fig. 19.10 is only observed if and only if the actual outbreak location is chosen as the center perspective node. In other words, if the temporal snapshots are depicted using a different reference node the concentric pattern is scrambled and irregular. Therefore, one can use the effective distance method to identify the outbreak location of a spreading process based on a single temporal snapshot. This method is illustrated in a proof-of-concept example depicted in Fig. 19.12. Assume that we are given a temporal snapshot of a spreading process as depicted in Fig. 19.12a and the goal is to reconstruct the outbreak origin from the data. Conventional geometric considerations are not sucessful because the network-driven processes generically do not yields simple geometric patterns. Using effective distance, we can now investigate the pattern from the perspective of every single potential outbreak location. We could for example pick a set of candidate outbreak locations (panel (b) in the figure). If this is done we will find that only for one candidate outbreak location the temporal snapshot has the shape of a concentric circle. This must be the original outbreak location. This process, qualitatively depicted in the figure, can be applied in a quantitative way and has been applied to actual epidemic data such as the 2011 EHEC outbreak in Germany [28].

Fig. 19.12

Outbreak reconstruction using effective distance. a The panel depicts a temporal snapshot of a computer simulated hypothetical pandemic, red dots denote airports with a high prevalence of cases. From the snapshot alone it is difficult to assess the outbreak origin which in this case is ORD (Chicago). b A choice of 12 potential outbreak locations as candidates. c For these candidate locations the pattern is depicted in the effective distance perspective. Only for the correct outbreak location the pattern is concentric. This method can be used quantitatively to identify outbreaks of epidemics that initially spread in a covert way

8 Conclusions

Emergent infectious diseases that bear the potential of spreading across the globe are an illustrative example of how connectivity in a globalized world has changed the way human mediated processes evolve in the 21st century. We are connected by complex networks of interaction, mobility being only one of them. With the onset of social media, the internet and mobile devices we share information that proliferates and spreads on information networks in much the same way (see also Chap. 20). In all of these systems the scientific challenge is understanding what topological and statistical features of the underlying network shape particular dynamic features observed in natural systems. The examples addressed above focus on a particular scale, defined by a single mobility network, the air-transportation network that is relevant for this scale. As more and more data accumulates, computational models developed in the future will be able to integrate mobility patterns at an individual resolution, potentially making use of pervasive data collected on mobile devices and paving the way towards predictive models that can account very accurately for observed contagion patterns. The examples above also illustrate that just feeding better and faster computers with more and more data may not necessarily help understanding the fundamental processes and properties of the processes that underly a specific dynamic phenomenon. Sometimes we only need to change the conventional and traditional ways of looking at patterns and adapt our viewpoint appropriately.