Abstract
One of the most important facts about operators on finite dimensional spaces equipped with a scalar product is the spectral theorem which says that a self-adjoint operator m can be written as a linear combination
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
A measure space ( Ω, μ) is semifinite if the measure μ is semifinite, i.e. for any measurable Δ ⊂ Ω such that μ( Δ) > 0 there exists a measurable Λ ⊂ Δ such that 0 < μ( Λ) + ∞.
- 2.
The fact that \(\mathfrak {M}\) is a σ-algebra is rather obvious. Moreover, it turns out that \(\mathfrak {M}\) is nothing else, but the σ-algebra of Borel subsets of Ω. Indeed: clearly any open subset of Ω belongs to \(\mathfrak {M}\), so that \(\mathfrak {M}\) contains all Borel sets. On the other hand if Δ is a Borel subset of Ω then for each j ∈ J the set Δj can be identified with Δ ∩({j}× σ(x)). This identification comes from the homeomorphism
$$\displaystyle \begin{aligned} \sigma(x)\ni\lambda\longmapsto(j,\lambda)\in\{j\}\times\sigma(x), \end{aligned}$$which, of course, preserves the Borel structure. It follows that each Δj is a Borel subset of σ(x).
- 3.
A ∗-homomorphism is a linear, multiplicative and ∗-preserving map. A homomorphism Φ : A →B between unital algebras is called unital when
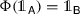. - 4.
More precisely, elements of \(\mathscr {H}\big (\sigma (x)\big )\) are equivalence classes of the equivalence relation identifying functions which coincide on some neighborhood of σ(x).
.References
W. Arveson, An Invitation to C∗-Algebras (Springer, New York, 1976)
W. Arveson, A Short Course of Spectral Theory (Springer, New York, 2002)
P. Halmos, A Hilbert Space Problem Book (Springer, New York, 1982)
M. Reed, B. Simon, Methods of Modern Mathematical Physics I. Functional Analysis (Academic Press, London, 1980)
W. Rudin, Functional Analysis (McGraw-Hill, New York, 1991)
W. Żelazko, Banach Algebras (Polish Scientific Publishers, Warsaw, 1973)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Sołtan, P. (2018). Spectral Theorems and Functional Calculus. In: A Primer on Hilbert Space Operators. Compact Textbooks in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-92061-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-92061-0_4
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-92060-3
Online ISBN: 978-3-319-92061-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)
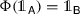