Abstract
Software Fault Isolation (SFI) consists in transforming untrusted code so that it runs within a specific address space, (called the sandbox) and verifying at load-time that the binary code does indeed stay inside the sandbox. Security is guaranteed solely by the SFI verifier whose correctness therefore becomes crucial. Existing verifiers enforce a very rigid, almost syntactic policy where every memory access and every control-flow transfer must be preceded by a sandboxing instruction sequence, and where calls outside the sandbox must implement a sophisticated protocol based on a shadow stack. We propose to define SFI as a defensive semantics, with the purpose of deriving semantically sound verifiers that admit flexible and efficient implementations of SFI. We derive an executable analyser, that works on a per-function basis, which ensures that the defensive semantics does not go wrong, and hence that the code is well isolated. Experiments show that our analyser exhibits the desired flexibility: it validates correctly sandboxed code, it catches code breaking the SFI policy, and it can validate programs where redundant instrumentations are optimised away.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This exploits the property that the range of the sandbox is a power of 2.
References
Balakrishnan, G., Reps, T.: Analyzing memory accesses in x86 executables. In: Duesterwald, E. (ed.) CC 2004. LNCS, vol. 2985, pp. 5–23. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24723-4_2
Biondi, P., Rigo, R., Zennou, S., Mehrenberger, X.: BinCAT: purrfecting binary static analysis. In: Symposium sur la sécurité des technologies de l’information et des communications (2017)
Brumley, D., Jager, I., Avgerinos, T., Schwartz, E.J.: BAP: a binary analysis platform. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 463–469. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_37
Dullien, T., Porst, S.: REIL: a platform-independent intermediate representation of disassembled code for static code analysis. In: CanSecWest 2009 (2009)
Haas, A., et al.: Bringing the web up to speed with WebAssembly. In: Proceedings of the 38th Conference on Programming Language Design and Implementation, pp. 185–200. ACM (2017)
Jourdan, J.-H., Laporte, V., Blazy, S., Leroy, X., Pichardie, D.: A formally-verified C static analyzer. In: Proceedings of the 42nd Symposium on Principles of Programming Languages, pp. 247–259. ACM (2015)
Kinder, J.: Static analysis of x86 executables. Ph.D. thesis, Technische Universität Darmstadt, November 2010
Kroll, J.A., Stewart, G., Appel, A.W.: Portable software fault isolation. In: Proceedings of the 27th IEEE Computer Security Foundations Symposium, pp. 18–32. IEEE (2014)
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7), 107–115 (2009)
Mihaila, B.: Adaptable static analysis of executables for proving the absence of vulnerabilities. Ph.D. thesis, Technische Universität München (2015)
Miné, A.: Abstract domains for bit-level machine integer and floating-point operations. In: Proceedings of the Workshops on Automated Theory eXploration and on Invariant Generation. EPiC Series in Computing, vol. 17, pp. 55–70. EasyChair (2012)
Morrisett, G., Tan, G., Tassarotti, J., Tristan, J.-B., Gan, E.: RockSalt: better, faster, stronger SFI for the x86. SIGPLAN Not. 47(6), 395–404 (2012)
Sehr, D., et al.: Adapting software fault isolation to contemporary CPU architectures. In: Proceedings of the 19th USENIX Conference on Security, pp. 1–12. USENIX (2010)
Shoshitaishvili, Y., et al.: SoK: (state of) the art of war: offensive techniques in binary analysis. In: IEEE Symposium on Security and Privacy (2016)
Wahbe, R., Lucco, S., Anderson, T.E., Graham, S.L.: Efficient software-based fault isolation. SIGOPS Oper. Syst. Rev. 27(5), 203–216 (1993)
Yee, B., et al.: Native client: a sandbox for portable, untrusted x86 native code. Commun. ACM 53(1), 91–99 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Concrete Operational Semantics

B Intra-procedural Semantics

C Proof of Lemma 1
First we need an intermediate lemma:
Lemma 3
(Base pointer is contained).
Proof
We reason by induction on \(S \in Acc\). In the initial state, we have \(bp = s_0 - {\textsc {gz}}_\top \) and \(\beta = 0\), so the property is true since \(s_s > {\textsc {gz}}_\top + {\textsc {gz}}_\bot \).
In the inductive case, we procede by case analysis on  , where S verifies the property. Because the property only depends on the context and \(\beta \), most cases are trivial: they preserve the context and \(\beta \). In the case of the StoreFrame rule, the context is preserved, and \(\beta \) is updated to 1. The property is still preserved because the property when \(\beta =0\) implies the property when \(\beta = 1\).
, where S verifies the property. Because the property only depends on the context and \(\beta \), most cases are trivial: they preserve the context and \(\beta \). In the case of the StoreFrame rule, the context is preserved, and \(\beta \) is updated to 1. The property is still preserved because the property when \(\beta =0\) implies the property when \(\beta = 1\).
The last case is when the extended call rule applies. In that case, \(\beta (S) = 1\), \(bp(S') = bp(S) - \mid \phi _1 \mid \) with \( \mid \phi _1 \mid \le f_s\) and \(\beta (S') = 0\).
Since \(s_0 - s_s + {\textsc {gz}}_\bot < bp(S) \le s_0 - {\textsc {gz}}_\top \), \(s_0 - s_s + {\textsc {gz}}_\bot - \mid \phi _1 \mid < bp(S') \le s_0 - {\textsc {gz}}_\top \), so \(s_0 - s_s + {\textsc {gz}}_\bot - f_s < bp(S') \le s_0 - {\textsc {gz}}_\top \) and the property holds.
Now we can prove the main lemma:
Proof
First, we prove that \( Acc \subseteq \gamma ({\textit{I}}\hbox {-} {\textit{Acc}})\).
Let \(S \in Acc \). By induction on S, we have the following cases:
-
\(S = \langle \varGamma _0,\varSigma _0 \rangle = \langle \langle [\langle s_0, \phi _i \rangle ] , s_0-{\textsc {gz}}_\top , \rho _0 \rangle , \langle \rho ,\delta ,\phi ^{(0)},\iota _0 \rangle \rangle \) with \( \mid \phi _i \mid = {\textsc {gz}}_\top \).
By definition, \(\iota _0 \in \mathcal {F}\), so we can construct \(Init(\iota _0)\). By construction, \(S \in \gamma (Init(\iota _0))\).
-
\(S = \langle \varGamma _2, \varSigma _2 \rangle \text { with } \langle \varGamma _1, \varSigma _1 \rangle \in Acc \) and
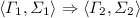 . By induction hypothesis, we also have \(S^\natural \) such that \(\langle \varGamma _1, \varSigma _1 \rangle \in \gamma (S^\natural )\).
. By induction hypothesis, we also have \(S^\natural \) such that \(\langle \varGamma _1, \varSigma _1 \rangle \in \gamma (S^\natural )\).Since \({\textit{I}}\hbox {-}{\textit{Safe}}({\textit{I}}\hbox {-} {\textit{Acc}})\), \(S^\natural \rightarrow ^\natural S_2^\natural \).
By case analysis on the rule that allows \(\rightarrow ^\natural \), we have:
-
(FunAssign) The preconditions are the same as for (Assign), so there is \(S'\) such that \(S \rightarrow ^\natural S'\). Furthermore, \(S' \in \gamma (s'^{\sharp })\).
-
(FunStD, FunLdD, FunCont, FunIndirectJump, FunHalt, FunCrash)
Similar reasoning.
-
(FunStF) Here, the preconditions are either true for (StoreFrame) or (StoreCrash) because of Lemma 3, so there is \(S'\) such that \(S \rightarrow ^\natural S'\), with \(S' = \blacksquare \) (writing in the guard zone) or \(S' = \langle \rho ,\delta ,\phi ^{(\beta )},\iota \rangle \) (writing in the frame). Furthermore, \(S' \in \gamma (s'^{\sharp })\).
-
(FunLdS) Here, the preconditions are either true for (LoadStack) or (LoadCrash) because of Lemma 3, so there is \(S'\) such that \(S \rightarrow ^\natural S'\), with \(S' = \blacksquare \) (reading in the guard zone) or \(S' = \langle \rho ,\delta ,\phi ^{(\beta )},\iota \rangle \) (reading in the stack). Futhermore, \(S' \in \gamma (s'^{\sharp })\).
-
(FunCall) Here the preconditions are the same as for (CallAcc) because of Lemma 3, so there is \(S'\) such that
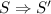 . Furthermore, \(S' \in \gamma _s(Init(f)) \subseteq \gamma _s(S^{\sharp })\).
. Furthermore, \(S' \in \gamma _s(Init(f)) \subseteq \gamma _s(S^{\sharp })\). -
(FunRet) Here the preconditions are the same as for (RetAcc), so
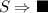 . Furthermore, \(\blacksquare \in \gamma (s'^{\sharp })\).
. Furthermore, \(\blacksquare \in \gamma (s'^{\sharp })\).
-
Hence our intermediate conclusion: \( Acc \subseteq \gamma ({\textit{I}}\hbox {-} {\textit{Acc}})\).
Let’s now take \(S \in Acc \). We use the previous conclusion to also choose \(S^\natural \in {\textit{I}}\hbox {-} {\textit{Acc}}\) such that \(S \in \gamma (S^\natural )\). Because we have \({\textit{I}}\hbox {-}{\textit{Safe}}({\textit{I}}\hbox {-} {\textit{Acc}})\), we can also take \(S_2^\natural \) such that \(S^\natural \rightarrow S_2^\natural \).
By case analysis with a similar reasoning as the previous property, we get that  with \(S' \in \gamma (S_2^\natural )\).
with \(S' \in \gamma (S_2^\natural )\).
Hence \( Safe ( Acc )\).
D Proof of Lemma 2
Proof
First, we prove that \({\textit{I}}\hbox {-} {\textit{Acc}}\subseteq \gamma ({\textit{A}}\hbox {-} {\textit{Acc}})\).
Let \(S \in {\textit{I}}\hbox {-} {\textit{Acc}}\). By induction on S, we have the following cases:
-
\(S \in Init(f) = \langle \langle \phi _i, bp, \rho \rangle , \langle \rho ,\phi ^{(f)},0 \rangle \rangle \)
We can construct \(S^\sharp = \langle \langle \phi _i', bp, \rho ' \rangle , \langle \rho ',\phi '^{(f)},0 \rangle \in AInit(f)\) such that \(S \in \gamma (S^\sharp )\).
\(S^\sharp \in {\textit{A}}\hbox {-} {\textit{Acc}}\), so the property is true in that case.
-
\(S = \langle \varGamma , \varSigma _2 \rangle \text { with } \langle \varGamma , \varSigma _1 \rangle \in {\textit{I}}\hbox {-} {\textit{Acc}}\text { and } \varGamma \vdash \varSigma _1 \rightarrow ^\natural \varSigma _2\). By induction hypothesis, we also have \(S^\sharp \) such that \(\langle \varGamma _1, \varSigma _1 \rangle \in \gamma (S^\sharp )\).
Because we have \({\textit{A}} \hbox {-} {\textit{Safe}}({\textit{A}}\hbox {-} {\textit{Acc}})\), we also have \(S_2^\sharp \) such that \(S^\sharp \rightarrow S_2^\sharp \).
By case analysis on \(\rightarrow \), we can see as before that the preconditions of the abstract semantics are the same or more restrictive than those of the intra procedural semantics. It is also built in a way that \(\langle \varGamma , \varSigma _2 \rangle \in \gamma (S_2^\sharp )\).
Hence our intermediate conclusion: \({\textit{I}}\hbox {-} {\textit{Acc}}\subseteq \gamma ({\textit{A}}\hbox {-} {\textit{Acc}})\).
Let’s now take \(S \in {\textit{I}}\hbox {-} {\textit{Acc}}\). We use the previous conclusion to also choose \(S^\sharp \in {\textit{A}}\hbox {-} {\textit{Acc}}\) such that \(S \in \gamma (S^\sharp )\). Because we have \({\textit{A}} \hbox {-} {\textit{Safe}}({\textit{A}}\hbox {-} {\textit{Acc}})\), we can also take \(S_2^\sharp \) such that \(S^\sharp \rightarrow S_2^\sharp \).
By case analysis with a similar reasoning as the previous property, we get that  with \(S' \in \gamma (S_2^\sharp )\).
with \(S' \in \gamma (S_2^\sharp )\).
Hence \( Safe ({\textit{I}}\hbox {-} {\textit{Acc}})\).
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Besson, F., Jensen, T., Lepiller, J. (2018). Modular Software Fault Isolation as Abstract Interpretation. In: Podelski, A. (eds) Static Analysis. SAS 2018. Lecture Notes in Computer Science(), vol 11002. Springer, Cham. https://doi.org/10.1007/978-3-319-99725-4_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-99725-4_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-99724-7
Online ISBN: 978-3-319-99725-4
eBook Packages: Computer ScienceComputer Science (R0)


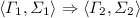 . By induction hypothesis, we also have
. By induction hypothesis, we also have 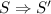 . Furthermore,
. Furthermore, 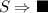 . Furthermore,
. Furthermore,