Skip to main content
SpringerLink
Log in

Circulations

  • Chapter
Graphs, Networks and Algorithms

Part of the book series: Algorithms and Computation in Mathematics ((AACIM,volume 5))

Abstract

In Chap. 6, we considered the simplest kind of ow problems, namely the determination of maximal ows in a network, in considerable detail; and in Chap. 7, we studied various important applications of this theory. The present chapter deals with generalizations of the

ows we worked with so far. For example, quite often there are also lower bounds on the capacities of the edges given; or one may seek a maximal ow which is optimal with respect to a given cost function on the edges. To solve these (and even more general) problems, it proves helpful to remove the exceptional role of the source and sink vertices s and t by requiring the ow preservation condition for all vertices, including s and t. This leads to the notion of circulations on directed graphs. As we will see, there are many interesting applications of this more general concept. To a large part, these cannot be treated using the theory of maximal ows as presented before; nevertheless, the methods of Chap. 6 will serve as fundamental tools for the more general setting. We shall begin with a rather thorough theoretical investigation of circulations and then develop efficient algorithms for finding an optimal circulation (or showing that no such circulation can exist); this turns out to be considerably more difficult than determining an ordinary maximal ow. Finally, as an application of circulations, we shall also consider the construction of rather good codes (a mathematical concept used to deal with data corruption by allowing the correction of errors) using the cycle spaces of graphs.

Round and round the circle…

T. S. Eliot

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 54.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 69.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    We may assume, without loss of generality, that ts is not an edge of G; otherwise, we could subdivide ts into two edges.

  2. 2.

    As usual, ∞ stands for a sufficiently large number, for example \(\sum_{e^{-}=s} c(e)\).

  3. 3.

    The requirement b(r)=0 guarantees that only flows with a non-negative value correspond to feasible circulations. Note that we need to add the condition w(f)≥0 to the definition in terms of flows, as trivial examples show. We certainly do not want to consider flows with a negative value, as these would (intuitively) correspond to a flow in the reverse direction, namely from t to s.

  4. 4.

    The cycle space of a graph is a special case of a more general construction assigning certain modules to any geometry; see [GhiJu90] and the references given there.

  5. 5.

    We note that the out-of-kilter algorithm is polynomial if we include the capacities in the calculation of the size of the input data: for a natural number z, we may take log2 z as a measure for the size of z. Algorithms which are polynomial in our sense (that is, their complexity is independent of the capacity constraints and the cost function) are often called strongly polynomial in the literature. For this property, all numbers occurring during the algorithm have to be polynomial in the total size of the input data. This is trivially true if the algorithm involves only additions, subtractions, comparisons, and multiplications or divisions by a constant factor. We will sometimes call algorithms which are polynomial in |E|, |V|, and the logarithm of the size of the input data weakly polynomial.

  6. 6.

    A similar argument shows that we do not need parallel edges; indeed, we have always excluded parallel edges in our study of flows and circulations.

  7. 7.

    Of course, c is not completely arbitrary: we should have −c(v,u)≤c(u,v); otherwise, there are no feasible circulations on N.

  8. 8.

    Note that the transformation we have described tacitly assumes that pairs of antiparallel edges in the original digraph have the same cost; otherwise, the elimination technique used makes no sense. While this assumption will be satisfied in many applications, we can use the following little trick if it should be violated: for each pair of antiparallel edges with different costs, we subdivide one of the edges into two edges and then assign to both new edges the same capacities and half the cost of the original edge.

  9. 9.

    For an intuitive interpretation of a circulation in the new sense, consider only its positive part—which lives on a network without antiparallel edges.

  10. 10.

    Note that the following transformation has the same form as the one used in Eq. (10.7).

  11. 11.

    This optimality criterion for potentials is one example for how the different way of description used in this section simplifies the technical details of our presentation. Of course, an analogous criterion can be proved using the standard notation for a network (G,b,c). However, we would then need three conditions which have to be satisfied for all edges uv∈E:

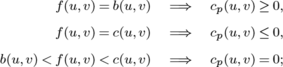
    see [AhuMO93], p. 330. These conditions are called complementary slackness conditions; they are a special case of the corresponding conditions used in linear programming. It may be checked that the potentials p(v) correspond to the dual variables if the problem of determining an optimal circulation is written as a linear program.

  12. 12.

    In our context, the terms mean cost or mean length would make more sense; however, we do not want to deviate from common usage.

  13. 13.

    Sometimes, there are upper bounds placed also on the capacities of the edges.

  14. 14.

    The author of the present book thinks that the most intuitive way to become acquainted with problems of combinatorial optimization is the presentation in a graph theory context; however, the theory of linear programming is indispensable for further study.

  15. 15.

    [Gro85, §8.2] shows an actual example where a chain of transactions resulting in a gain occurs.

  16. 16.

    In everyday language, a code usually means a way of secret communication: for instance, one speaks of breaking a code. However, the corresponding part of mathematics is cryptography, whereas coding theory deals with the problem of ensuring that information can be recovered accurately after transmission or storage, in spite of possible loss or corruption of data; there is no aspect of secrecy involved. To use the words of Claude Shannon [Sha48a, Sha48b], the founder of information theory (who, by the way, also put cryptography onto a sound mathematical basis in his paper [Sha49b]), of which coding theory is one part:

    The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.

    Codes in this sense constitute a spectacularly successful part of applied mathematics: satellite images, CD’s, DVD’s, digital TV, mobile phones all need codes (to mention just a few examples). In this context, we also recommend another introduction to coding theory, namely [VanOo89], where the reader may find a nice description of the mathematical principles underlying compact discs.

  17. 17.

    This is precisely the approach used for transmitting pictures from one of the early satellites, namely Mariner 9. The injection chosen in this case made it possible to correct up to seven errors per codeword, which was sufficient to make an incorrect decoding very unlikely; see [Pos69] for details.

  18. 18.

    Note that we may reconstruct x uniquely from y and the error pattern E, provided that we are in the binary case.

  19. 19.

    Finite fields are an important tool in many applications, not just in coding theory, but also in cryptography, signal processing, geometry, and design theory, as well as in algebraic graph theory and matroid theory, to mention just some examples. It is known that the cardinality of a finite field has to be a prime power q, and that there is—up to isomorphism—exactly one finite field with q elements (for every prime power q), which is usually denoted by GF(q). For background on finite fields, we refer the reader to the standard text book [LidNi94] or to [McEl87] for an introduction requiring very little algebraic knowledge; both of these books also discuss some interesting applications.

References

  1. Ahuja, R.K., Goldberg, A.V., Orlin, J.B., Tarjan, R.E.: Finding minimum-cost flows by double scaling. Math. Program. 53, 243–266 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ahuja, R.K., Magnanti, T.L., Orlin, J.B.: Network Flows: Theory, Algorithms and Applications. Prentice Hall, Englewood Cliffs (1993)

    MATH  Google Scholar 

  3. Arkin, E.M., Papadimitriou, C.H.: On the complexity of circulations. J. Algorithms 7, 134–145 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  4. Barahona, F., Tardos, E.: Note on Weintraub’s minimum-cost circulation algorithm. SIAM J. Comput. 18, 579–583 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  5. Berge, C., Ghouila-Houri, A.: Programmes, Jeux et Réseaux de Transport. Dunod, Paris (1991)

    Google Scholar 

  6. Berlekamp, E.R., McEliece, R.J., van Tilborg, H.C.A.: On the inherent intractability of certain coding problems. IEEE Trans. Inf. Theory 24, 384–386 (1978)

    Article  MATH  Google Scholar 

  7. Bierbrauer, J.: Introduction to Coding Theory. Chapman & Hall/CRC, Boca Raton (2005)

    MATH  Google Scholar 

  8. Bobrow, L.S., Hakimi, S.L.: Graph theoretic q-ary codes. IEEE Trans. Inf. Theory 17, 215–218 (1971)

    Article  MATH  Google Scholar 

  9. Bollobás, B.: Extremal Graph Theory. Academic Press, New York (1978)

    MATH  Google Scholar 

  10. Bredeson, J.G., Hakimi, S.L.: Decoding of graph theoretic codes. IEEE Trans. Inf. Theory 13, 348–349 (1967)

    Article  MATH  Google Scholar 

  11. Busacker, R.G., Gowen, P.J.: A procedure for determining a family of minimum cost flow networks. ORO Techn. Report 15, John Hopkins University (1961)

    Google Scholar 

  12. Chvátal, V.: Linear Programming. Freeman, New York (1983)

    MATH  Google Scholar 

  13. Costa, M., Létocart, L., Roupin, F.: Minimal multicut and maximal integer multiflow: a survey. Eur. J. Oper. Res. 162, 55–69 (2005)

    Article  MATH  Google Scholar 

  14. Deo, N., Prabhu, G.M., Krishnamoorthy, M.S.: Algorithms for generating fundamental cycles in a graph. ACM Trans. Math. Softw. 8, 26–42 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  15. Edmonds, J., Karp, R.M.: Theoretical improvements in algorithmic efficiency for network flow problems. J. Assoc. Comput. Mach. 19, 248–264 (1972)

    Article  MATH  Google Scholar 

  16. Ervolina, T.R., McCormick, S.T.: Two strongly polynomial cut cancelling algorithms for minimum cost network flow. Discrete Appl. Math. 46, 133–165 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  17. Fleischer, L., Skutella, M.: Quickest flows over time. SIAM J. Comput. 36, 1600–1630 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ford, L.R., Fulkerson, D.R.: Constructing maximal dynamic flows from static flows. Oper. Res. 6, 419–433 (1958)

    Article  MathSciNet  Google Scholar 

  19. Ford, L.R., Fulkerson, D.R.: Flows in Networks. Princeton University Press, Princeton (1962)

    MATH  Google Scholar 

  20. Fujishige, S.: An O(m 3logn) capacity-rounding algorithm for the minimum-cost circulation problem: A dual framework of Tardos’ algorithm. Math. Program. 35, 298–308 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  21. Fulkerson, D.R.: An out-of-kilter method for minimal cost flow problems. J. Soc. Ind. Appl. Math. 9, 18–27 (1961)

    Article  MATH  Google Scholar 

  22. Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18, 1013–1036 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  23. Galil, Z., Tardos, E.: An O(n 2(m+nlogn)logn) min-cost flow algorithm. J. Assoc. Comput. Mach. 35, 374–386 (1986)

    Article  MathSciNet  Google Scholar 

  24. Ghinelli, D., Jungnickel, D.: The Steinberg module of a graph. Arch. Math. 55, 503–506 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  25. Glover, F., Klingman, D., Phillips, N.V.: Network Models in Optimization and Their Applications in Practice. Wiley, New York (1992)

    Book  Google Scholar 

  26. Goldberg, A.V., Tarjan, R.E.: Finding minimum-cost circulations by canceling negative cycles. J. Assoc. Comput. Mach. 36, 873–886 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  27. Goldberg, A.V., Tarjan, R.E.: Solving minimum cost-flow problems by successive approximation. Math. Oper. Res. 15, 430–466 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  28. Goldberg, A.V., Plotkin, S.A., Tardos, E.: Combinatorial algorithms for the generalized circulation problem. Math. Oper. Res. 16, 351–381 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  29. Goldfarb, D., Jin, Z., Lin, Y.: A polynomial dual simplex algorithm for the generalized circulation problem. Math. Program. 91, 271–288 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  30. Gondran, M., Minoux, N.: Graphs and Algorithms. Wiley, New York (1984)

    MATH  Google Scholar 

  31. Grötschel, M.: Operations Research I. Lecture Notes, Universität Augsburg (1985)

    Google Scholar 

  32. Hakimi, S.L.: Recent progress and new problems in applied graph theory. In: Proc. IEEE Region Six Annual Conf., pp. 635–643 (1966)

    Google Scholar 

  33. Hakimi, S.L., Bredeson, J.G.: Graph theoretic error-correcting codes. IEEE Trans. Inf. Theory 14, 584–591 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  34. Hakimi, S.L., Bredeson, J.G.: Ternary graph theoretic error-correcting codes. IEEE Trans. Inf. Theory 15, 435–436 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  35. Hakimi, S.L., Frank, H.: Cut set matrices and linear codes. IEEE Trans. Inf. Theory 11, 457–458 (1965)

    Article  Google Scholar 

  36. Herz, J.C.: Cours de Théorie des Graphes. Faculté des Sciences de Lille (1967)

    Google Scholar 

  37. Hitchcock, F.L.: The distribution of a product from several sources to numerous localities. J. Math. Phys. 20, 224–230 (1941)

    MathSciNet  Google Scholar 

  38. Hoffman, A.J.: Some recent applications of the theory of linear inequalities to extremal combinatorial analysis. In: Bellman, R.E., Hall, M. (eds.) Combinatorial Analysis, pp. 113–127. Am. Math. Soc., Providence (1960)

    Google Scholar 

  39. Horton, J.D.: A polynomial time algorithm to find the shortest cycle basis of a graph. SIAM J. Comput. 16, 358–366 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  40. Jarrah, A.I.Z., Yu, G., Krishnamurthy, N., Rakshit, A.: A decision support framework for airline flight cancellations and delays. Transp. Sci. 27, 266–280 (1993)

    Article  Google Scholar 

  41. Jungnickel, D., Vanstone, S.A.: An application of coding theory to a problem in graphical enumeration. Arch. Math. 65, 461–464 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  42. Jungnickel, D., Vanstone, S.A.: Graphical codes—a tutorial. Bull. Inst. Comb. Appl. 18, 45–64 (1996)

    MathSciNet  MATH  Google Scholar 

  43. Jungnickel, D., Vanstone, S.A.: Graphical codes revisited. IEEE Trans. Inf. Theory 43, 136–146 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  44. Jungnickel, D., Vanstone, S.A.: Ternary graphical codes. J. Comb. Math. Comb. Comput. 29, 17–31 (1999)

    MathSciNet  MATH  Google Scholar 

  45. Jungnickel, D., Vanstone, S.A.: q-ary graphical codes. Discrete Math. 208/209, 375–386 (1999)

    Article  MathSciNet  Google Scholar 

  46. Karp, R.M.: Reducibility among combinatorial problems. In: Miller, R.E., Thatcher, J.W. (eds.) Complexity of Computer Computations, pp. 85–103. Plenum Press, New York (1972)

    Chapter  Google Scholar 

  47. Karp, R.M.: A characterization of the minimum cycle mean in a digraph. Discrete Math. 23, 309–311 (1978)

    MathSciNet  MATH  Google Scholar 

  48. Klein, M.: A primal method for minimal cost flows, with applications to the assignment and transportation problems. Manag. Sci. 14, 205–220 (1967)

    Article  MATH  Google Scholar 

  49. Lawler, E.L.: Combinatorial Optimization: Networks and Matriods. Holt, Rinehart and Winston, New York (1976)

    Google Scholar 

  50. Lidl, R., Niederreiter, H.: Introduction to Finite Fields and Their Applications, revised edn. Cambridge University Press, Cambridge (1994)

    Book  MATH  Google Scholar 

  51. Lomonosov, M.V.: Combinatorial approaches to multiflow problems. Discrete Appl. Math. 11, 1–93 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  52. MacWilliams, F.J., Sloane, N.J.A.: The Theory of Error-Correcting Codes. North Holland, Amsterdam (1977)

    MATH  Google Scholar 

  53. McEliece, R.J.: Finite Fields for Computer Scientists and Engineers. Kluwer, Boston (1987)

    Book  MATH  Google Scholar 

  54. Minty, G.J.: Monotone networks. Proc. R. Soc. Lond. A 257, 194–212 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  55. Minty, G.J.: On the axiomatic foundations of the theories of directed linear graphs, electrical networks and network programming. J. Math. Mech. 15, 485–520 (1966)

    MathSciNet  MATH  Google Scholar 

  56. Orlin, J.B.: A faster strongly polynomial minimum cost flow algorithm. Oper. Res. 41, 338–350 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  57. Orlin, J.B.: A polynomial time primal network simplex algorithm for minimum cost flows. Math. Program. 78, 109–129 (1997)

    MathSciNet  MATH  Google Scholar 

  58. Orlin, J.B., Ahuja, R.K.: New scaling algorithms for the assignment and minimum cycle mean problems. Math. Program. 54, 41–56 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  59. Orlin, J.B., Plotkin, S.A., Tardos, E.: Polynomial dual network simplex algorithms. Math. Program. 60, 255–276 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  60. Posner, E.C.: Combinatorial structures in planetary reconnaissance. In: Mann, H.B. (ed.) Error Correcting Codes, pp. 15–46. Wiley, New York (1969)

    Google Scholar 

  61. Radzik, T., Goldberg, A.V.: Tight bounds on the number of minimum mean cycle cancellations and related results. In: Proc. 2nd ACM—SIAM Symp. on Discrete Algorithms, pp. 110–119 (1991)

    Google Scholar 

  62. Read, R.C.: Euler graphs on labeled nodes. Can. J. Math. 14, 482–486 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  63. Restrepo, M., Williamson, D.P.: A simple GAP-canceling algorithm for the generalized maximum flow problem. Math. Program. 118, 47–74 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  64. Seymour, P.: Sums of circuits. In: Bondy, J.A., Murty, U.S.R. (eds.) Graph Theory and Related Topics, pp. 341–355. Academic Press, New York (1979)

    Google Scholar 

  65. Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948) (Part I)

    MathSciNet  MATH  Google Scholar 

  66. Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27, 623–656 (1948) (Part II)

    MathSciNet  Google Scholar 

  67. Shannon, C.E.: Communication theory of secrecy systems. Bell Syst. Tech. J. 28, 656–715 (1949)

    MathSciNet  MATH  Google Scholar 

  68. Tardos, E.: A strongly polynomial minimum cost circulation algorithm. Combinatorica 5, 247–255 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  69. Tardos, E.: A strongly polynomial algorithm to solve combinatorial linear programs. Oper. Res. 34, 250–256 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  70. Tarjan, R.E.: Dynamic trees as search trees via Euler tours applied to the network simplex algorithm. Math. Program. 78, 169–177 (1997)

    MathSciNet  MATH  Google Scholar 

  71. van Lint, J.H.: Introduction to Coding Theory, 3rd edn. Springer, Berlin (1999)

    Book  MATH  Google Scholar 

  72. van Lint, J.H., Wilson, R.M.: A Course in Combinatorics, 2nd edn. Cambridge University Press, Cambridge (2001)

    Book  MATH  Google Scholar 

  73. Vanstone, S.A., van Oorschot, P.C.: An Introduction to Error Correcting Codes with Applications. Kluwer, Boston (1989)

    MATH  Google Scholar 

  74. Weintraub, A.: A primal algorithm to solve network flow problems with convex costs. Manag. Sci. 21, 87–97 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  75. Young, N.E., Tarjan, R.E., Orlin, J.B.: Faster parametric shortest path and minimum-balance algorithms. Networks 21, 205–221 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  76. Zadeh, N.: A bad network problem for the simplex method and other minimum cost flow algorithms. Math. Program. 5, 255–266 (1973)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Mathematik, Universität Augsburg, Augsburg, Germany

    Dieter Jungnickel

Authors
  1. Dieter Jungnickel
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Berlin Heidelberg

About this chapter

Cite this chapter

Jungnickel, D. (2013). Circulations. In: Graphs, Networks and Algorithms. Algorithms and Computation in Mathematics, vol 5. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-32278-5_10

Download citation

Publish with us

Policies and ethics

Search

Navigation