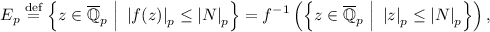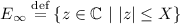Keywords

1 Introduction

Coppersmith’s method [Cop97, Cop01] is a celebrated technique in public-key cryptanalysis for finding small roots of polynomial equations modulo integers. In the simplest case, one is given a degree-d monic polynomial f(x) with integer coefficients, and one wishes to find the integers r modulo a given integer N for which \(f(r) \equiv 0 \bmod N\). When N is prime, this problem can be efficiently solved in polynomial time, but for composite N of unknown factorization, no efficient method is known in general. In fact, such an algorithm would immediately break the RSA cryptosystem, by allowing one to decrypt ciphertexts c by finding roots of the polynomial \(f(x) = x^e - c \bmod N\).

While it appears intractable to solve this problem in polynomial time, Coppersmith showed that one can efficiently find all small integers r such that \(f(r) \equiv 0\) mod N. More precisely, he proved the following result in [Cop97]:

Theorem 1

(Coppersmith 1996). Suppose one is given a modulus N and a monic polynomial \(f(x) = x^d + f_{d-1} x^{d-1} + \cdots + f_1 x + f_0\) in \( \mathbb {Z}[x]\). One can find all \(r \in \mathbb {Z}\) such that

$$\begin{aligned} |r| \le N^{1/d}\quad \mathrm {and} \quad f(r) \equiv 0 \bmod N \end{aligned}$$
(1)

in polynomial time in \(\mathrm {log}(N) + \sum _i \log |f_i|\).

The algorithm he developed to prove this result has applications across public-key cryptography, including cryptanalysis of low public exponent RSA with fixed-pattern or affine padding [Cop97], the security proof of RSA-OAEP [Sho01], and showing that the least significant bits of RSA are hardcore [SPW06]. We discuss these applications in more detail in Sect. 2.3. If the exponent 1/d in the bound in Eq. 1 could be increased, it would have immediate practical impact on the security of a variety of different cryptosystems.

In followup work, [Cop01, Sect. 4] Coppersmith speculates about possible improvements of this exponent 1/d. The main conclusion of [Cop01, Sect. 4] is that “We have tried to abuse this method to obtain information that should otherwise be hard to get, and we always fail.” We discuss these obstructions in more detail in Sect. 2.2.

Later, the hardness of finding roots of f(x) of size \(N^{1/d+\epsilon }\) for \(\epsilon > 0\) was formalized as a concrete cryptographic hardness assumption [SPW06].

Coppersmith’s proof of Theorem 1 relies on constructing a polynomial h(x) such that any small integer r satisfying \(f(r) \equiv 0 \bmod N\) is a root of h(x) over the integers. He finds such an auxiliary polynomial h(x) by constructing a basis for a lattice of polynomials, and then by using the Lenstra-Lenstra-Lovasz lattice basis reduction algorithm [LLL82] to find a “small” polynomial in this lattice. The smallness condition ensures that any small integer r satisfying \(f(r) \equiv 0\) mod N must be a root of h(x). The algorithm then checks which rational roots r of h(x) have the desired properties.

Our Results. In this paper, our main result is that one cannot increase the exponent 1/d in Coppersmith’s theorem by using auxiliary polynomials of the kind he considers. We give a formal proof that there do not exist polynomials of the kind required to extend Coppersmith’s theorem by the same method, regardless of the polynomial p(x), the modulus N, and the method used to find them. This is a much more general statement than previous partial results along these lines, and in particular it applies to the settings of most interest to cryptographers. This eliminates possible improvements to the method using improvements in lattice algorithms or shortest vector bounds. We obtain our results by drawing a new connection between this family of cryptographic techniques and results from the capacity theory of adelic subsets of algebraic curves. We will use fundamental results of Cantor [Can80] and Rumely [Rum89, Rum13] about capacity theory to prove several results about such polynomials.

In particular, we will prove in Theorem 6 a stronger form of the following result. This result shows that there are no polynomials of the type used by Coppersmith that could lead to an improvement of the bound in (1) from \(N^{1/d}\) to \(N^{1/d+\epsilon }\) for any \(\epsilon > 0\).

Theorem 2

(Optimality of Coppersmith’s Theorem). Let f be a monic polynomial of degree d. Suppose \(\epsilon > 0\). There does not exist a non-zero polynomial \(h(x) \in \mathbb {Q}[x]\) of the form

$$\begin{aligned} h(x) = \sum _{i,j \ge 0} a_{i,j} \ x^i \ (f(x)/N)^j \end{aligned}$$
(2)

with \(a_{i,j} \in \mathbb {Z}\) such that \(|h(z)| < 1\) for all z in the complex disk \(\{z \in \mathbb {C}: |z| \le N^{(1/d) + \epsilon } \}\). Furthermore, if \(\epsilon > \ln (2)/\ln (N)\) there is no such h(x) such that \(|h(z)| < 1\) for all z in the real interval \([-N^{1/d + \epsilon }, N^{1/d +\epsilon }]\).

Note that in order for Coppersmith’s method to run in polynomial time, h(x) should have degree bounded by a polynomial in \(\ln (N)\). Theorem 2 says that when \(\epsilon > 0\) there are no polynomials of any degree satisfying the stated bounds. We can thus eliminate the possibility of an improvement to this method with even superpolynomial running time.

In [Cop01], Coppersmith already noted that it did not appear possible to improve the exponent 1/d in his result by searching for roots in the real interval \([-N^{1/d+\epsilon },N^{1/d +\epsilon }]\) instead of in the complex disk of radius \(N^{1/d+\epsilon }\). The last statement in Theorem 2 quantifies this observation, since \(\ln (2)/\ln (N) \rightarrow 0\) as \(N \rightarrow \infty \).

Coppersmith also notes that since the binomial polynomials

$$ b_i(x) = x \cdot (x-1) \cdots (x - i + 1)/i! $$

take integral values on integers, one could replace \(x^i\) in (2) by \(b_i(x)\) and \((f(x)/N)^j\) by \(b_j(f(x)/N)\). Coppersmith observed (backed up by experiments) that this leads to a small improvement on the size of the root that can be found, and a speedup for practical computations. The improvement is proportional to the degree of the auxiliary polynomial h(x) that is constructed, and is thus limited for a polynomial-time algorithm.

We show that the exponent 1/d in Coppersmith’s theorem still cannot be improved using binomial polynomials, but for a different reason. Our results come in two parts. First, we show that the exact analogue of Theorem 2 is false in the case of integral combinations of binomial polynomials. In fact, there are such combinations that have all the properties required in the proof of Coppersmith’s theorem. The problem is that these polynomials have very large degree, and in fact, they vanish at every small integer, not just the solutions of the congruence. This is formalized in the following theorem, which is a simplified version of Theorem 9.

Theorem 3

(Existence of Binomial Auxiliary Polynomials). Suppose \(\delta \) is any positive real number. For all sufficiently large integers N there is a non-zero polynomial of the form \(h(x) = \sum _i a_{i} \ b_i(x) \) with \(a_i \in \mathbb {Z}\) such that \(|h(z)| < 1\) for all z in the complex disk \(\{z \in \mathbb {C}: |z| \le N^{\delta } \}\).

Second, we show that the existence of these polynomials still does not permit cryptographically useful improvements to Coppersmith’s bound beyond \(N^{1/d}\). This is because if one is able to use binomial polynomials of small degree to obtain such an improvement, then the modulus N must have a small prime factor. In that case, it would have been more efficient to factor N and use the factorization to find the roots. More precisely, we will show in Theorem 11 a stronger form of the following result:

Theorem 4

(Negative Coppersmith Theorem for Binomial Polynomials). Let f be a monic polynomial of degree d. Suppose \(\epsilon > 0\) and that M and N are integers with \(1.48774 N^\epsilon \ge M \ge 319\). If there is a non-zero polynomial h(x) of the form

$$\begin{aligned} h(x) = \sum _{0 \le i,j \le M} a_{i,j} \ b_i(x) \ b_j(f(x)/N) \end{aligned}$$
(3)

with \(a_{i,j} \in \mathbb {Z}\) such that \(|h(z)| < 1\) for z in the complex disk \(\{z \in \mathbb {C}: |z| \le N^{1/d+ \epsilon } \}\), then N must have a prime factor less than or equal to M. In particular, this will be the case for all large N if we let \(M = \ln (N)^c\) for some fixed integer \(c > 0\).

Note that the integer M quantifies “smallness” in Theorem 4 in two ways. First, it is a bound on the degree of the binomial polynomials that are allowed to be used to create auxiliary polynomials. But then if a useful auxiliary polynomial exists, then N must have a factor of size less than or equal to M. As a special case of Theorem 4, if \(N = pq\) is an RSA modulus with two large equal sized prime factors, then any auxiliary polynomial of the form in (3) that can find roots of size \(N^{1/d+\epsilon }\) must involve binomial terms with i or j at least \(1.48774N^{\epsilon }\).

Note that Coppersmith’s theorem in its original form is not sensitive to whether or not N has small prime factors. Theorem 4 shows that the existence of useful auxiliary polynomials does depend on whether N has such small factors.

The paper is organized in the following way. In Sect. 2.1 we begin by recalling Coppersmith’s algorithm for finding small solutions of polynomial congruences. In Sect. 2.3 we recall some mathematical hardness assumptions and we discuss their connection to the security of various cryptosystems and Coppersmith’s algorithm. In Sect. 3 we review some basic notions from algebraic number theory, and we recall some results of Cantor [Can80] and Rumely [Rum89, Rum13] on which our work is based. At the end of Sect. 3 we prove Theorem 6, which implies Theorem 2. We state and prove Theorems 9 and 11 in Sect. 4; these imply Theorems 3 and 4. One of the goals of this paper is to provide a framework for using capacity theory to show when these auxiliary polynomials do or do not exist. We give an outline in Sect. 5 of how one proves these types of results. In the conclusion we summarize the implications of our results and discuss possible directions for future research.

2 Background and Related Work

Given a polynomial \(f(x) = x^d + f_{d-1} x^{d-1} + \cdots + f_1 x + f_0 \in \mathbb {Z}[x]\) and a prime p we can find solutions \(x \in \mathbb {Z}\) to the equation

$$\begin{aligned} f(x) \equiv 0 \bmod p \end{aligned}$$
(4)

in randomized polynomial time using e.g. Berlekamp’s algorithm or the Cantor-Zassenhaus algorithm [Ber67, CZ81]. While it is “easy” to find roots of f(x) in the finite field \(\mathbb {Z}/p\mathbb {Z}\) and over \(\mathbb {Z}\) as well, there is no known efficient method to find roots of f(x) modulo N for large composite integers N unless one knows the factorization of N.

2.1 Coppersmith’s Method

Although finding roots of a univariate polynomial, f(x), modulo N is difficult in general, if f(x) has a “small” root, then this root can be found efficiently using Coppersmith’s method [Cop97].

Coppersmith’s method for proving Theorem 1 works as follows. We follow the exposition in [Cop01], which incorporates simplifications due to Howgrave-Graham [HG97]. Suppose \(\epsilon > 0\) and that f(x) has a root \(r \in \mathbb {Z}\) with \(|r| \le N^{1/d - \epsilon } \) and \(f(r) \equiv 0\) mod N. He considers the finite rank lattice \(\mathcal {L}\) of rational polynomials in \(\mathbb {Q}[x]\) of the form

$$ h_{ij}(x) = \sum _{0 \le i+dj < t} a_{i,j} \ x^i \ (f(x)/N)^{j} $$

where \(t \ge 0\) is an integer parameter to be varied and all \(a_{i,j} \in \mathbb {Z}\). Here \(\mathcal {L}\) is a finite rank lattice because the denominators of the coefficients of \(h_{ij}(x)\) are bounded and \(h_{ij}(x)\) has degree bounded by t.

If we evaluate any polynomial \(h_{ij} \in \mathcal {L}\) at a root r satisfying \(f(r) \equiv 0 \bmod N\), \(h_{ij}(r)\) will be an integer.

Concretely, one picks a basis for a sublattice of \(\mathcal {L} \in \mathbb {Q}^{t-1}\) by taking a suitable set of polynomials \(\{h_{ij}(x)\}_{i,j}\) and representing each polynomial by its coefficient vector. Coppersmith’s method applies the LLL algorithm to this sublattice basis to find a short vector representing a specific polynomial, \(h_\epsilon (x)\) in \(\mathcal {L}\). He shows that the fact that the vector of coefficients representing \(h_\epsilon (x)\) is short implies that \(|h_{\epsilon }(x)| < 1\) for all \(x \in \mathbb {C}\) with \(|x| \le N^{1/d - \epsilon }\), and that for sufficiently large t, the LLL algorithm will find a short enough vector. Because \(h_\epsilon (x)\) is an integral combination of terms of the form \(x^i (f(x)/N)^j\), this forces \(h(r) \in \mathbb {Z}\) because \(f(r)/N \in \mathbb {Z}\). But \(|r| \le N^{1/d - \epsilon }\) forces \(|h_\epsilon (r)| < 1\). Because 0 is the only integer less than 1 in absolute value, we see \(h_\epsilon (r) = 0\). So r is among the zeros of \(h_\epsilon (x)\), and as discussed earlier, there is an efficient method to find the integer zeros of a polynomial in \(\mathbb {Q}[x]\). One then lets \(\epsilon \rightarrow 0\) and does a careful analysis of the computational complexity of this method.

The bound in Theorem 1 arises from cleverly choosing a subset of the possible \(\{h_{ij}\}\) as a lattice basis so that one can bound the determinant of the lattice as tightly as possible, then using the LLL algorithm in a black-box way on the resulting lattice basis.

2.2 Optimality of Coppersmith’s Theorem

Since Coppersmith’s technique uses the LLL algorithm [LLL82] to find the specific polynomial h(x) in the lattice \(\mathcal {L}\), it is natural to think that improvements in lattice reduction techniques or improved bounds on the length of the shortest vector in certain lattices might improve the bound \(N^{1/d}\) in Theorem 1.

Such an improvement would be impossible in polynomial time for arbitrary N, since the polynomial \(f(x) = x^d\) has exponentially many roots modulo \(N=p^d\) of absolute value \(N^{1/d+\epsilon }\), but this does not rule out the possibility of improvements for cases of cryptographic interest, such as polynomial congruences modulo RSA moduli \(N = pq\).

Coppersmith [Cop01] finds “cause for pessimism” in extending his technique. This pessimism comes from a specific example where the modulus N is equal to \(q^3\) the cube of a prime q. He observes that there are exponentially many small solutions to the congruence in question for such moduli, so his method cannot be expected to work in a black box manner for all moduli. He explains “we expect trouble whenever \(q^2\) divides N and p(x) has repeated roots mod q.” Since RSA moduli are square-free, Coppersmith’s counterexample does not apply to RSA moduli. In general, Coppersmith’s pessimism comes from examples where the discriminant of f(x) and N share a prime factor—in which case we can factor N using a simple GCD calculation. Thus Coppersmith’s counterexamples will never apply to any hard-to-factor modulus N. Coppersmith left open the possibility that his method could be improved for the applications of most interest to cryptographers. More explicitly, after discussing the above examples, he supposes he is not in the “unfavorable situation” in which the discriminant of p(x) and N have a common factor, and he discusses a “discriminant attack” which might work in this case. To say that the discriminant of p(x) and N have no common factor is the same as saying there are integer polynomials D(x) and E(x) together with an integer F such that \(D(x) p(x) + E(x) p'(x) + FN = 1\). Coppersmith wrote “Perhaps D, E, F can be incorporated into the construction of the lattice L, in such a way that the bound B can be improved to \(N^{1/d + \epsilon }\). But I don’t see how to do it.” Our results show that such an improvement is impossible.

Aono, Agrawal, Satoh, and Watanabe [AASW12] showed that Coppersmith’s lattice basis construction is optimal under the heuristic assumption that the lattice behaves as a random lattice; however they left open whether improved lattice bounds or a non-lattice-based approach to solving this problem could improve the \(N^{1/d}\) bound.

2.3 Cryptanalytic Applications of Coppersmith’s Theorem

Theorem 1 has many immediate applications to cryptanalysis, particularly the cryptanalysis of RSA. May [May07] gives a comprehensive survey of cryptanalytic applications of Coppersmith’s method. In this paper, we focus on Coppersmith’s method applied to univariate polynomials modulo integers. We highlight several applications of the univariate case below.

The RSA assumption posits that it is computationally infeasible to invert the map \(x \mapsto x^d \bmod N\), i.e., it is infeasible to find roots of \(f(x) = x^d - c \bmod N\). Because of their similar structure, almost all of the cryptographically hard problems (some of which are outlined below) based on factoring can be approached using Coppersmith’s method (Theorem 1).

Low public exponent RSA with stereotyped messages: A classic example listed in Coppersmith’s original paper [Cop97] is decrypting “stereotyped” messages encrypted under low public exponent RSA, where an approximation to the solution is known in advance. The general RSA map is \(x \mapsto x^e \bmod N\). For efficiency purposes, e can be chosen to be as small as 3, so that a “ciphertext” is \(c_0 = x_0^3 \bmod N\). Suppose we know some approximation to the message \(\tilde{x}_0\) to the message \(x_0\). Then we can set

$$ f(x) = (\tilde{x}_0 + x)^3 - c. $$

Thus f(x) has a root (modulo N) at \(x = x_0 - \tilde{x}_0\). If \(|x_0 - \tilde{x}_0| < N^{1/3}\) then this root can be found using Coppersmith’s method.

Security of RSA-OAEP: The RSA function \(x \mapsto x^e \bmod N\) is assumed to be a one-way trapdoor permutation. Optimal Asymmetric Encryption Padding (OAEP) is a general method for taking a one-way trapdoor permutation and a random oracle [BR93], and creating a cryptosystem that achieves security against adaptive chosen ciphertext attacks (IND-CCA security).

Instantiating the OAEP protocol with the RSA one-way function yields RSA-OAEP, a standard cryptosystem. When the public exponent is \(e = 3\), Shoup used Coppersmith’s method to show that RSA-OAEP is secure against an adaptive chosen-ciphertext attack (in the random oracle model) [Sho01].

Hard-core bits of the RSA Function: Repeated iteration of the RSA function has been proposed as candidate for a pseudo random generator. In particular, we can create a stream of pseudo random bits by picking an initial “seed”, \(x_0\) and calculating the series

$$\begin{aligned} x_i&\mapsto x_{i+1} \\ x_i&\mapsto x_i^e \bmod N \end{aligned}$$

At each iteration, the generator will output the r least significant bits of \(x_i\). For efficiency reasons, we would like r to be as large as possible while still maintaining the provable security of the generator.

When we output only 1 bit per iteration, this was shown to be secure [ACGS88, FS00], and later this was increased to allow the generator to output any \(\log \log (N)\) consecutive bits [HN04]. The maximum number of bits that can be safely outputted by such a generator is tightly tied to the approximation \(\tilde{x}\) necessary for recovering x from \(x^e \bmod N\). Thus a bound on our ability to find small roots of \(f(x) = (x-\tilde{x})^e -c \bmod N\) immediately translates into bounds on the maximum number of bits that can be safely outputted at each step of the RSA pseudo random generator.

In order to construct a provably secure pseudo random generator that outputs \(\varOmega (n)\) pseudo random bits for each multiplication modulo N, [SPW06] assume there is no probabilistic polynomial time algorithm for solving the \( \left( \frac{1}{d} + \epsilon , d \right) \)-SSRSA problem.

Definition 1

(The \((\delta ,d)\) -SSRSA Problem [SPW06]). Given a random n bit RSA modulus, N and a polynomial \(f(x) \in \mathbb {Z}[x]\) with \({\text {deg}}(f) = d\), find a root \(x_0\) such that \(|x_0| < N^{\delta }\).

Coppersmith’s method solves the \( \left( \frac{1}{d}, d \right) \)-SSRSA Problem. Our results show that Coppersmith’s method cannot be used to solve the \( \left( \frac{1}{d} + \epsilon , d \right) \)-SSRSA problem. Note that our results do not prove that the \( \left( \frac{1}{d}+\epsilon ,d \right) \)-SSRSA problem is intractable—doing so would imply there is no polynomial-time algorithm for factoring—but instead we show that the best available class of techniques cannot be extended.

Extensions to Coppersmith’s Method. Coppersmith’s original work also considered the problem of finding small solutions to polynomial equations in two variables over the integers and applied his results to the problem of factoring RSA moduli \(N=pq\) when half of the most or least significant bits of one of the factors p is known [Cop97]. Howgrave-Graham gave an alternate formulation of this problem by finding approximate common divisors of integers using similar lattice-based techniques, and obtained the same bounds for factoring with partial information [HG01]. May [May10] gives a unified formulation of Coppersmith and Howgrave-Graham’s results to find small solutions to polynomial equations modulo unknown divisors of integers. Later work by Jutla [Jut98] and Jochemsz and May [JM06] has generalized Coppersmith’s method to multivariate equations, and Herrmann and May [HM08] obtained results for multivariate equations modulo divisors.

As we will show in the next section, existing results in capacity theory can be used to directly address the case of auxiliary polynomials for Coppersmith’s method for univariate polynomials modulo integers. Adapting these results to the other settings of Coppersmith’s method listed above is a direction for future research.

3 Capacity Theory for Cryptographers

In this section, we begin by recalling from [Can80, Rum89, Rum13] some background about arithmetic capacity theory, which is the tool we will use to prove our main results.

Classically, capacity theory arose from the following problem in electrostatics. How will a unit charge distribute itself so as to minimize potential energy if it is constrained to lie within a compact subset \(E_\infty \) of \(\mathbb {C}\) which is stable under complex conjugation? Define the capacity \(\gamma (E_\infty )\) to be \(e^{-V(E_\infty )}\), where \(V(E_\infty )\) is the so-called Robbin’s constant giving the minimal potential energy of a unit charge distribution on \(E_\infty \).

It was discovered by Fekete and Szegő [Fek23, FS55] that the distribution of small charges on such an E is related to the possible locations of zeros of monic integral polynomials. Heuristically, these zeros behave in the same way as charges that repel one another according to an inverse power law.

The nth transfinite diameter of a set \(E_{\infty }\) is

$$ d_n(E_{\infty }) = \sup _{z_1 \dots z_n \in E} \prod _{i < j} |z_i - z_j|^{1/\left( {\begin{array}{c}n\\ 2\end{array}}\right) }. $$

Then we can give a second definition of the capacity of \(E_{\infty }\) as follows. It can be shown that this definition of capacity is equivalent to the definition via electrostatics.

Definition 2

(Capacity of a Set via the Transfinite Diameter).

$$\begin{aligned} \gamma (E_{\infty }) = \lim _{n \rightarrow \infty } d_n(E_{\infty }) \end{aligned}$$

Let \(z_1, \dots , z_n\) be the conjugates of a degree-n algebraic integer. Then they are the roots of the monic irreducible polynomial \(f(x) = \prod _{i=1}^n(x-z_i) \in \mathbb {Z}[x]\). The discriminant of f(x) is the non-zero rational integer \(\varDelta f(x) = \prod _{i<j}(z_i-z_j)^2\). Therefore the nth transfinite diameter of a set \(E_{\infty }\) that contains the \(z_i\) satisfies

$$ d_n(E_{\infty }) \ge \prod _{i < j} |z_i - z_j|^{\frac{2}{n(n-1)}} = | \varDelta f(x) |^{\frac{1}{n(n-1)}} \ge 1 $$

Thus \(d_n(E_{\infty }) \ge 1\) if E contains all conjugates of a degree-n algebraic integer. Since \(E_{\infty }\) is bounded, only finitely many algebraic integers of degree n have all their conjugates in E. Thus if there are infinitely many algebraic integers with all conjugates in \(E_{\infty }\) then \(\gamma (E_{\infty }) \ge 1\). The restriction that the discriminant of a monic integral polynomial without multiple zeros must be a non-zero integer prevents all the zeros from being too close to one another. Since the discriminant of the polynomial has absolute value at least 1, the potential energy is not positive.

The capacity can also be defined using the Chebyshev constant. Consider the set of degree-n polynomials bounded on \(E_{\infty }\):

$$ b_n = \sup \left\{ |r| \mid \exists p(x) = rx^n + \dots + p_0 \in \mathbb {R}[x] \,\text {s.t.}\, \sup _{z \in E_{\infty }} |p(z)| \le 1 \right\} . $$

Definition 3

(Capacity of a set via the Chebyshev Constant).

$$ \gamma (E_{\infty }) = \lim _{n \rightarrow \infty } b_n^{-1/n} $$

A final equivalent definition of the capacity is the sectional capacity (see [Chi91, RLV00]). Consider the set of polynomials with real coefficients whose evaluations are bounded on \(E_{\infty }\):

$$ F_n = \{ p(x) \in \mathbb {R}[x] \mid \deg p(x) \le n, \sup _{z \in E} |p(z)| < 1 \} $$

\(F_n\) is a convex symmetric subset of \(\mathbb {R}^{n+1}\).

Definition 4

(Sectional Capacity).

$$ \log \gamma (E) = \lim _{n \rightarrow \infty } \frac{-2 \log {\text {Vol}}(F_n)}{n^2} $$

If \(\gamma (E) < 1\) then for large n, we have \(\log {\text {Vol}}(F_n) \approx (-n^2/2) \log \gamma (E) > (n+1) \log 2\). If \({\text {Vol}}(F_n) > 2^{n+1}\) then by Minkowski’s theorem there must be a non-zero polynomial \(p(x) \in F_n \cap \mathbb {Z}[x]\). Consider again \(z_1, \dots , z_n\) that are conjugates of some degree-n algebraic integer in \(E_{\infty }\). We have \(|p(z_1)|, \dots , |p(z_n)| < 1\), so \(\mathrm {Norm}(p(z_1)) = \prod _i |p(z_i)| < 1\), where \(\mathrm {Norm}\) is the norm from \(\mathbb {Q}(z_1)\) to \(\mathbb {Q}\). But \(\mathrm {Norm}(p(z_1))\) is a rational integer, so \(\mathrm {Norm}(p(z_1)) = 0\) and \(p(z_1) = 0\). Therefore the zeros of p(x) include all algebraic integers with conjugates in this set, and thus p(x) must vanish at all such elements in E.

These intuitions are behind the following striking result of Fekete and Szegő from [Fek23, FS55].

Theorem 5

(Fekete and Szegő). Let \(E_{\infty }\) be a compact subset of \(\mathbb {C}\) closed under complex conjugation.

  • If \(\gamma (E_\infty ) < 1\), then there are only finitely many irreducible monic polynomials with integer coefficients which have all of their roots in \(E_\infty \).

  • Conversely, if \(\gamma (E_\infty ) > 1\), then for every open neighborhood U of \(E_\infty \) in \(\mathbb {C}\), there are infinitely many irreducible monic polynomials with integer coefficients having all their roots in U.

The first case corresponds to the case in which the minimal potential energy \(V(E_\infty )\) is positive, consistent with the physical intuition.

The work of Fekete and Szegő was vastly generalized by Cantor [Can80] to adelic subsets of the projective line, and by Rumely [Rum89, Rum13] to adelic subsets of arbitrary smooth projective curves over global fields. Their methods are based on potential theory, as in electrostatics. In [Chi91], Chinburg suggested sectional capacity theory, which applies to arbitrary regular projective varieties of any dimension and not just to curves. Sectional capacity theory was based on ideas from Arakelov theory, with the geometry of numbers and Minkowski’s theorem being the primary tools. In [RLV00], Rumely, Lau and Varley showed that the limits hypothesized in [Chi91] do exist under reasonable hypotheses; this is a deep result.

This paper is the first application of capacity theory that we are aware of to cryptography. We will show that capacity theory is very suited to studying the kind of auxiliary polynomials used in the proof of Coppersmith’s theorem. Before we begin, however, we review some number theory.

3.1 p-adic Numbers

For any prime p, and any \(n \in \mathbb {Z}\), we define the p-adic valuation of n, to be the supremum of the integers e such that \(p^e | n\), i.e.,

$$ v_p(n) = \left\{ \begin{array}{ll} \max \left\{ e \in \mathbb {Z}: p^e \mid n \right\} &{} \text{ if } n \ne 0 \\ \infty &{} \text{ if } n = 0 \end{array} \right. $$

This is then extended to rational numbers in the natural way. If \(a,b \in \mathbb {Z}\) and \(a,b \ne 0\), then

$$ v_p \left( \frac{a}{b} \right) = v_p(a) - v_p(b). $$

The p-adic valuation gives rise to a p-adic absolute value \(| \ |_p:\mathbb {Q}\rightarrow \mathbb {R}\) given by

$$\begin{aligned} \left| x \right| _p = \left\{ \begin{array}{ll} p^{-v_p(x)} &{} \text{ if } x \ne 0 , \\ 0 &{} \text{ if } x = 0 . \end{array} \right. \end{aligned}$$
(5)

It is straightforward to check that the p-adic absolute value is multiplicative and satisfies a stronger form of the triangle inequality:

$$\begin{aligned} \left| xy \right| _p = \left| x \right| _p\cdot \left| y \right| _p \quad \mathrm {and} \quad \left| x+y \right| _p \le \max \left( \left| x \right| _p, \left| y \right| _p \right) \quad \mathrm {for} \quad x, y \in \mathbb {Q}. \end{aligned}$$
(6)

The p-adic absolute value defines a metric on \(\mathbb {Q}\). The p-adic numbers, \(\mathbb {Q}_p\), are defined to be the completion of \(\mathbb {Q}\) with respect to this metric. This is similar to the construction of \(\mathbb {R}\) as the completion of \(\mathbb {Q}\) with respect to the Euclidean absolute value \(|\ |:\mathbb {Q}\rightarrow \mathbb {R}\).

Elements of \(\mathbb {Q}_p\) are either 0 or expressed in a unique way as a formal infinite sum

$$ \sum _{i=k}^\infty a_i p^i $$

in which \(k \in \mathbb {Z}\), each \(a_i\) lies in \(\{0,1,\ldots ,p-1\}\) and \(a_k \ne 0\). Such a sum converges to an element of \(\mathbb {Q}_p\) because the sequence of integers \(\{s_j\}_{j = k}^\infty \) defined by \(s_j = \sum _{i = k}^j a_i p^i\) forms a Cauchy sequence with respect to the metric \(| \ |_p\). One can add, subtract and multiply such sums by treating p as a formal variable, performing operations in the resulting formal power series ring in one variable over \(\mathbb {Z}\), and by then carrying appropriately. In fact, \(\mathbb {Q}_p\) is a field, since multiplication is commutative and it is possible to divide elements by non-zero elements of \(\mathbb {Q}_p\).

A field L is algebraically closed if every non-constant polynomial \(g(x) \in L[x]\) has a root in L. This implies that g(x) factors into a product of linear polynomials in L[x], since one can find in L roots of quotients of g(x) by products of previously found linear factors. For example, \(\mathbb {C}\) is algebraically closed, but \(\mathbb {Q}\) is certainly not.

In general, given a field F there are many algebraically closed fields L containing F. For example, given one such L, one could simply label the elements of L by the elements of some other set, or one could put L inside a larger algebraically closed field. Given one L, the set \(\overline{F}\) of elements \(\alpha \in L\) which are roots in L of some polynomial in F[x] is called the algebraic closure of F in L. The set \(\overline{F}\) is in fact an algebraically closed field. For a given F, the algebraic closure \(\overline{F}\) will depend on the algebraically closed field L which one chooses in this construction. But if one were to use a different field \(\tilde{L}\), say, then the algebraic closure of F in \(\tilde{L}\) is isomorphic to \(\overline{F}\) by a (non-unique) isomorphism which is the identity on F. So we often just fix one algebraic closure \(\overline{F}\) of F.

For instance, if \(F = \mathbb {Q}\), then \(L = \mathbb {C}\) is algebraically closed, so we can take \(\overline{\mathbb {Q}}\) to be the algebraic closure of \(\mathbb {Q}\) in \(\mathbb {C}\). The possible field embeddings \(\tau :\overline{\mathbb {Q}} \rightarrow L = \mathbb {C}\) come from pre-composing with a field automorphism of \(\overline{\mathbb {Q}}\).

However, for each prime p, there is another alternative. The field \(\mathbb {Q}_p\) is not algebraically closed, but as noted above, we can find an algebraically closed field containing it and then construct the algebraic closure \(\overline{\mathbb {Q}}_p\) of \(\mathbb {Q}_p\) inside this field. Now we have \(\mathbb {Q} \subset \mathbb {Q}_p \subset \overline{\mathbb {Q}}_p\), and \(\overline{\mathbb {Q}}_p\) is algebraically closed. So we could take \(L = \overline{\mathbb {Q}}_p\) and consider the algebraic closure \(\overline{\mathbb {Q}}'\)of \(\mathbb {Q}\) inside \(\overline{\mathbb {Q}}_p\). We noted above that all algebraic closures of \(\mathbb {Q}\) are isomorphic over \(\mathbb {Q}\) in many ways. The possible isomorphisms of \(\overline{\mathbb {Q}}\) (as a subfield of \(\mathbb {C}\), for example) with \(\overline{\mathbb {Q}}'\) (as a subfield of \(\overline{\mathbb {Q}}_p\)) correspond to the field embeddings \(\sigma : \overline{\mathbb {Q}} \rightarrow \overline{\mathbb {Q}}_p\). Each such \(\sigma \) gives an isomorphism of \(\overline{\mathbb {Q}}\) with \(\overline{\mathbb {Q}}'\) which is the identity map on \(\mathbb {Q}\). Note here that \(\overline{\mathbb {Q}}_p\) is much larger than \(\overline{\mathbb {Q}}\), since \(\overline{\mathbb {Q}}_p\) (and in fact \(\mathbb {Q}_p\) as well) is uncountable while \(\overline{\mathbb {Q}}\) is countable.

Each \(\alpha \in \overline{\mathbb {Q}}\) is a root of a unique monic polynomial \(m_\alpha (x) \in \mathbb {Q}[x]\) of minimal degree, and \(m_\alpha (x)\) is irreducible. We will later need to discuss the image of such an \(\alpha \) under all the field embeddings \(\tau :\overline{\mathbb {Q}}\rightarrow \mathbb {C}\) and under all field embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\) as p varies. The possible values for \(\tau (\alpha )\) and \(\sigma (\alpha )\) are simply the different roots of \(m_\alpha (x)\) in \(\mathbb {C}\) and \(\overline{\mathbb {Q}}_p\), respectively.

Example 1

If \(\alpha = \sqrt{7}\) then \(m_\alpha (x) = x^2 - 7\). The possibilities for \(\tau (\alpha )\) are the positive real square root 2.64575... and the negative real square root \(-2.64575...\) of 7. When \(p = 3\), it turns out that \(x^2-7\) already has two roots \(\alpha _1\) and \(\alpha _2\) in the 3-adic numbers \(\mathbb {Q}_3 \subset \overline{\mathbb {Q}}_3\). These roots are

$$\alpha _1 = 1 + 1\cdot 3 + 1\cdot 3^2 + 0\cdot 3^3 + \cdots \quad \mathrm {and}\quad \alpha _2 = 2 + 1 \cdot 3 + 1 \cdot 3^2 + 2 \cdot 3^3 + \cdots .$$

These expansions result from choosing 3-adic digits so that the square of the right hand side of each equality is congruent to 1 modulo an increasing power of 3. This is the 3-adic counterpart of finding the decimal digits of the two real square roots of 7. So the possibilities for \(\sigma (\alpha )\) under all embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_3\) are \(\alpha _1\) and \(\alpha _2\).

Basic facts about integrality and divisibility are naturally encoded using p-adic absolute values:

Fact 1

As above, let \(\overline{\mathbb {Q}}_p\) denote an algebraic closure of \(\mathbb {Q}_p\). There is a unique extension of \(| \ |_p:\mathbb {Q}_p\rightarrow \mathbb {R}\) to an absolute value \(| \ |_p:\overline{\mathbb {Q}}_p\rightarrow \mathbb {R}\) for which (6) holds for all \(x, y \in \overline{\mathbb {Q}}_p\).

Fact 2

The set \(\overline{\mathbb {Z}}\) of algebraic integers is the set of all \(\alpha \in \overline{\mathbb {Q}}\) for which \(m_\alpha (x) \in \mathbb {Z}[x]\). In fact, \(\overline{\mathbb {Z}}\) is a ring, so that adding, subtracting and multiplying algebraic integers produces algebraic integers. One can speak of congruences in \(\overline{\mathbb {Z}}\) by saying \(\alpha \equiv \beta \) mod \(\gamma \overline{\mathbb {Z}} \) if \(\alpha - \beta = \gamma \cdot \delta \) for some \(\delta \in \overline{\mathbb {Z}}\).

Fact 3

If \(r \in \mathbb {Q}\) then \(\left| r \right| _p \le 1\) for all primes p if and only if \(r \in \mathbb {Z}\). More generally, an element \(\alpha \in \overline{\mathbb {Q}}\) is in \(\overline{\mathbb {Z}}\) if and only if for all primes p and all field embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\) one has \(|\sigma (\alpha )|_p \le 1\).

Fact 4

Suppose \(\alpha \in \overline{\mathbb {Z}}\) and \(|\tau (\alpha )| < 1\) for all embeddings \(\tau :\overline{\mathbb {Q}}\rightarrow \mathbb {C}\). Then in fact, \(\alpha = 0\). To see why, note that \(m_\alpha (0) \in \mathbb {Z}\) is ±1 times the product of the complex roots of \(m_\alpha (x)\). These roots all have the form \(\tau (\alpha )\), so \(|m_\alpha (0)| < 1\). Then \(m_\alpha (0) \in \mathbb {Z}\) forces \(m_\alpha (0) = 0\). Because \(m_\alpha (x)\) is monic and irreducible this means \(m_\alpha (x) = x\), so \(\alpha = 0\).

Fact 5

If \(N = pq\) for distinct primes p and q, then \(\left| N \right| _p = \frac{1}{p}\), \(\left| N \right| _{q} = \frac{1}{q}\), and \(\left| N \right| _{p'} = 1\) for all other primes \(p'\).

Fact 6

If \(a,b \in \mathbb {Z}\), then

$$ a | b \qquad \Leftrightarrow \qquad \left| b \right| _p \le \left| a \right| _p \quad \forall p $$

Thus a|b is the statement that b is in the p-adic disc of radius \(|a|_p\) centered at 0 for all p. More generally, if \(\alpha , \beta \in \overline{\mathbb {Z}}\) then \(\alpha \) divides \(\beta \) in \(\overline{\mathbb {Z}}\) if \(\beta = \delta \cdot \alpha \) for some \(\delta \in \overline{\mathbb {Z}}\). This is so if and only if \(|\sigma (\beta )|_p \le |\sigma (\alpha )|_p\) for all primes p and all field embeddings \(\sigma : \overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\).

3.2 Auxiliary Functions

The original question Coppersmith considered was this: Given an integer \(N \ge 1\), a polynomial f(x), and a bound X, can we find all integers \(z \in \mathbb {Z}\) such that \(|z| \le X\) and \(f(z) \equiv 0 \bmod N\)?

When X is sufficiently small in comparison to N, Coppersmith constructed a non-zero auxiliary polynomial of the form

$$\begin{aligned} h(x)=\sum _{i,j} a_{i,j}x^i(f(x)/N)^j,\qquad a_{i,j}\in \mathbb {Z}\end{aligned}$$
(7)

satisfying \(|h(z)|<1\) for every \(z\in \mathbb {C}\) with \(|z|\le X\). As noted in Sect. 2.1, this boundedness property forces the set of \(z\in \mathbb {Z}\) satisfying \(|z|\le X\) and \(f(z)\equiv 0\bmod N\) to be among the roots of h(x). In fact, the roots of the h(x) include all algebraic integers \(z \in \overline{\mathbb {Z}}\) satisfying

$$\begin{aligned} f(z) \equiv 0 \bmod N\cdot \overline{\mathbb {Z}}\quad \mathrm {and}\quad |\sigma (z)| \le X\quad \mathrm {for \ all \ embeddings}\quad \sigma : \overline{\mathbb {Q}}\rightarrow \mathbb {C}. \end{aligned}$$
(8)

The reason is as follows. For \(z\in \overline{\mathbb {Z}}\), the condition that \(f(z)\equiv 0\mod N\overline{\mathbb {Z}}\) is equivalent to the condition that \(f(z)/N\in \overline{\mathbb {Z}}\). Therefore, for any h(x) in the form of Eq. 7, we have \(h(z)\in \overline{\mathbb {Z}}\) whenever \(f(z)\equiv 0\bmod {N\overline{\mathbb {Z}}}\). If h(x) further satisfies \(|h(z)|<1\) for all \(z\in \mathbb {C}\) with \(|z|\le X\), then the property that \(|\sigma (z)|\le X\) for all embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \mathbb {C}\), means that \(|h(\sigma (z))|<1\) as well. Fact 4 therefore tells us that \(h(z)=0\).

Capacity theory can be used for solving the problem of deciding whether there exist non-zero auxiliary polynomials h(x) which include among its roots the set of \(z\in \overline{\mathbb {Z}}\) satisfying Eq. 8. The basic idea, which will be given in detail in Sect. 3.3, is that capacity theory gives one a way of deciding whether the set of algebraic integers satisfying Eq. 8 is finite or infinite.

When this set is infinite then there cannot exist any rational function h(x) of any kind vanishing on the \(z\in \overline{\mathbb {Z}}\) satisfying (8), and in particular no h(x) of the form in (7) will exist satisfying the desired properties. If, on the other hand, this set is finite then there will exist an auxiliary polynomial h(x) vanishing on the \(z\in \overline{\mathbb {Z}}\) satisfying (8), and in fact Coppersmith explicitly constructed such a polynomial using the LLL algorithm. As we will see, the boundary for finite versus infinite occurs when \(X=N^{1/d}\) where d is the degree of f(x).

3.3 When Do Useful Auxiliary Polynomials Exist?

In this section, we use capacity theory to give a characterization of when auxiliary polynomials h(x) of the kind discussed in Sect. 3.2 exist. We will use the work of Cantor in [Can80] to show the following result.

Theorem 6

(Existence of an Auxiliary Polynomial). Let d be the degree of f(x). Define S(X) to be the set of all algebraic integers \(z \in \overline{\mathbb {Z}}\) such that

$$ f(z) = 0 \bmod N \overline{\mathbb {Z}}\quad \mathrm {and}\quad |\sigma (z)| \le X\quad \mathrm {for \ all \ embeddings}\quad \sigma :\overline{\mathbb {Q}}\rightarrow \mathbb {C}. $$

There exists a polynomial \(h(x) \in \mathbb {Q}[x]\) whose roots include every element of S(X) if \(X < N^{1/d}\). If \(X > N^{1/d}\) there is no rational function \(h(x) \in \mathbb {Q}(x)\) whose zero set contains S(X) because S(X) is infinite.

We break the proof into a sequence of steps.

  1. 1.

    Since \(f(x) \in \mathbb {Z}[x]\), and embeddings fix integers, then if \(z \in \overline{\mathbb {Z}}\) we have \(f(z) \in \overline{\mathbb {Z}}\), and \(\sigma (f(x)) = f(\sigma (x))\) for all embeddings \(\sigma : \overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\).

  2. 2.

    Suppose \(N = p_1^{e_1} \cdots p_k^{e_k}\) and \(x \in \mathbb {Z}\), then by Fact 6

    $$\begin{aligned} f(z) \equiv 0 \bmod N&\Leftrightarrow \left| f(z) \right| _{p_i} \le \left( \frac{1}{p_i} \right) ^{e_i} \quad \forall i \in [k] \\&\Leftrightarrow \left| f(z) \right| _{p_i} \le \left| N \right| _{p_i} \quad \forall i \in [k] \end{aligned}$$

    Similarly, if \(z \in \overline{\mathbb {Z}}\) then

    $$\begin{aligned} f(z) = 0 \bmod N \overline{\mathbb {Z}}\Leftrightarrow |\sigma (f(z))|_{p_i} = \left| f(\sigma (z)) \right| _{p_i} \le \left| N \right| _{p_i} \end{aligned}$$

    for all \(i \in [k]\) and for all embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\).

  3. 3.

    For all primes, p, define the set of elements in \(\overline{\mathbb {Q}}_p\) that solve the congruence in Eq. 8 p-adically:

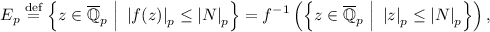
    and similarly define the set of elements with bounded complex absolute value

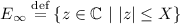
    Let

    This specifies the set of p-adic and complex constraints on our solutions. Furthermore, \(\mathbb {E}\) satisfies all of the conditions in [Rum89] for \(\mathbb {E}\) to have a well-defined capacity \(\gamma (\mathbb {E}) = \gamma (\mathbb {E},\{\infty \})\) relative to the point \(\infty \) on \(\mathbb {P}^1\), and for the computations below to be valid. Note, one requirement in this case is that for all but finitely many primes p, \(E_p\) is the integral closure \(\overline{\mathbb {Z}}_p\) of \(\mathbb {Z}_p\) in \(\overline{\mathbb {Q}}_p\). We will compute the capacity of \(\mathbb {E}\), a measurement of the size of \(\mathbb {E}\).

  4. 4.

    We now define the local capacities \(\gamma _p(E_p)\) and \(\gamma _\infty (E_\infty )\) as well as the global capacity \(\gamma (\mathbb {E})\). Suppose \(0 \le r \in \mathbb {R}\). We have p-adic and complex discs of radius r defined by

    and

Fact 7

(Capacity of a Disc). For \(v = p\) and \(v = \infty \), one has local capacity

$$ \gamma _v ( D_v(a,r) ) = r $$

If \(v = p\), \(a = 0\) and \(r = |N|_p\) is the p-adic absolute value of an integer \(N \ge 1\), then \(D_v(0,|N|_p) \cap \mathbb {Z}_p\) is just \(N \mathbb {Z}_p\). We will need later the fact that the p-adic capacity of \(N\mathbb {Z}_p\) is

$$\gamma _p(N\mathbb {Z}_p) = p^{-1/(p-1)} |N|_p$$

In a similar way, suppose \(v = \infty \). The capacity of the real interval \([-r,r]\) is

$$\gamma _\infty ([-r,r]) = r/2$$

Fact 8

(Capacity of Polynomial Preimage). If \(f(x) \in \mathbb {Z}[x]\) is a monic degree d polynomial, and S is a subset of \(\overline{\mathbb {Q}}_p\) if \(v = p\) or of \(\mathbb {C}\) if \(v = \infty \) for which the capacity \(\gamma _v(S)\) is well defined, then \(\gamma _v(f^{-1}(S))\) is well defined and

$$ \gamma _v \left( f^{-1}(S) \right) = \gamma _v(S)^{1/d} $$

Facts 7 and 8 show that

$$ \gamma _p( E_p ) = \gamma _p( D_p(0,\left| N \right| _p) )^{1/d} = |N|_p^{1/d}\quad \mathrm {and}\quad \gamma _\infty ( E_\infty ) = \gamma _p( D_\infty (0, X ) )= X. $$

Fact 9

(Capacity of a Product).

$$ \gamma (\mathbb {E}) = \gamma _\infty (E_\infty ) \cdot \prod _{p \in \text {primes}} \gamma _p(E_p) $$

So

$$\gamma (\mathbb {E}) = X \cdot \prod _{p \in \text {primes}} |N|_p^{1/d} = X \cdot \prod _{i = 1}^k p_i^{-e_i/d} = X \cdot N^{-1/d}.$$
  1. 5.

    Computing the capacity of our sets of interest tells us whether there exists a polynomial mapping the components of \(\mathbb {E}\) into discs of radius 1. This allows us to apply the following theorem, due to Cantor [Can80], which tells us when an auxiliary polynomial exists.

Theorem 7

(Existence of an Auxiliary Polynomial). If

$$ \mathbb {E}= E_\infty \times \prod _{p \in \text {primes}} E_p $$

then there exists a non-zero auxiliary polynomial \(h(x) \in \mathbb {Q}[x]\) satisfying

$$ h( E_p ) \subset D_p(0,1) \quad \forall p $$

and

if \(\gamma (\mathbb {E}) < 1\), and no such polynomial exists if \(\gamma (\mathbb {E}) > 1\).

Once we have set up this framework, we are now ready to prove Theorem 6.

Proof

(Proof of Theorem  6 ). Suppose first that \(X < N^{1/d}\). Then by Fact 9, \(\gamma (\mathbb {E}) < 1\). By Fact 7, there exists a polynomial \(h(x) \in \mathbb {Q}[x]\) with \(|h(z)|_p \le 1\) for all p and \(z \in E_p\), and \(|h(z)| < 1\) for all \(z \in E_\infty \). Suppose \(z \in S(X)\). Then \(f(z)/N \in \overline{\mathbb {Z}}\), so Fact 3 says that for all primes p and embeddings \(\sigma :\overline{\mathbb {Q}}\rightarrow \overline{\mathbb {Q}}_p\) one has

$$\left| \sigma (f(z)/N) \right| _p \le 1$$

Since \(f(x) \in \mathbb {Z}[x]\) and \(N \in \mathbb {Z}\), we have \(\sigma (f(z)) = f(\sigma (z))\) and \(\sigma (N) = N\). So

$$\left| f(\sigma (z)) \right| _p = \left| \sigma (f(z)) \right| _p = \left| \frac{\sigma (f(z))}{\sigma (N)} \right| _p \cdot \left| \sigma (N) \right| _p = \left| \sigma (f(z)/N) \right| _p \cdot \left| N \right| _p \le \left| N \right| _p.$$

Therefore \(\sigma (z) \in E_p\). Hence \(|h(\sigma (z))|_p \le 1\), where \(\sigma (h(z)) = h(\sigma (z))\) since \(h(x) \in \mathbb {Q}[x]\). Because p was an arbitrary prime, this means h(z) is an algebraic integer, i.e. \(h(z) \in \overline{\mathbb {Z}}\) by Fact 3. On the other hand, \(z \in S(X)\) implies \(|\sigma (z)| \le X\) so \(|\sigma (h(z))| = |h(\sigma (z))| < 1\) for all \(\sigma : \overline{\mathbb {Q}}\rightarrow \mathbb {C}\). Thus h(z) is an algebraic integer such that \(|\sigma (h(z))| < 1\) for all \(\sigma : \overline{\mathbb {Q}}\rightarrow \mathbb {C}\), so by Fact 4, \(h(z) = 0\) as claimed. When \(X > N^{1/d}\), S(X) is infinite by [Can80, Theorem 5.1.1].

To try to prove stronger results about small solutions of congruences, Coppersmith also considered auxiliary polynomials with absolute value less than 1 on a real interval which is symmetric about 0. We can quantify his observation that this does not lead to an improvement of the exponent 1/d in Theorem 1 by the following result.

Theorem 8

Let \(S'(X)\) be the subset of all \(z \in S(X)\) such that \(\sigma (z)\) lies in \(\mathbb {R}\) for every embedding \(\sigma :\overline{\mathbb {Q}}\rightarrow \mathbb {C}\). There exists a polynomial \(h(x) \in \mathbb {Q}[x]\) whose roots include every element of \(S'(X)\) if \(X < 2 N^{1/d}\). If \(X > 2 N^{1/d}\) there is no non-zero rational function \(h(x) \in \mathbb {Q}(x)\) whose zero set contains \(S'(X)\) because \(S'(X)\) is infinite.

Proof

(Proof of Theorem  8 ). To prove the Theorem 8, one just replaces the complex disc \(E_\infty = \{z \in \mathbb {C}: |z| \le X\}\) by the real interval \(E'_\infty = \{z \in \mathbb {R}:|z| \le X\}\). Letting \(\mathbb {E}' = \prod _p E_p \times E'_\infty \), we find \(\gamma (\mathbb {E}') = 2 \cdot \gamma (\mathbb {E})\) because \(\gamma (E'_\infty ) = 2 \gamma (E_\infty )\). So \(\gamma (\mathbb {E}') < 1\) if \(X < 2 N^{1/d}\) and we find as above that there is a polynomial \(h(x) \in \mathbb {Q}[x]\) whose roots contain every element of \(S(X)'\). If \(X > 2 N^{1/d}\) then \(\gamma (\mathbb {E}') > 1\) and \(S(X)'\) is infinite by the main result of [Rum13], so h(x) cannot exist.

4 Lattices of Binomial Polynomials

In this section, we will answer the question of whether Coppersmith’s theorem can be improved using auxiliary polynomials that are combinations of binomial polynomials. The results we proved in Sect. 3 showed that it is impossible to improve the bounds for auxiliary polynomials of the form \(h(x) = \sum _{i,j \ge 0} a_{i,j} x^i (f(x)/N)^j\).

Recall that if \(i \ge 0\) is an integer, the binomial polynomial \(b_i(x)\) is

$$ b_i(x) = x \cdot (x-1) \cdots (x - i + 1)/i!. $$

Based on a suggestion by Howgrave-Graham and Lenstra, Coppersmith considered in [Cop01] auxiliary polynomials constructed from binomial polynomials; that is, of the form

$$\begin{aligned} h(x) = \sum _{i,j \ge 0} a_{i,j} b_i(x) b_j(f(x)/N). \end{aligned}$$
(9)

He found that he was unable to improve the bound of \(N^{1/d}\) using this alternate lattice. In this section we will prove some sharper forms of Theorems 3 and 4 that explain why this is the case.

Following the method laid out in Sect. 3, we find that capacity theory cannot rule out the existence of such polynomials. One of the key differences is that monomials send algebraic integers to algebraic integers, while binomial polynomials do not because of the denominators. Therefore, we are no longer able to use the same sets \(E_p\) as in the previous section.

In fact, if one uses the lattice of binomial polynomials of the form (9), then for any disk in \(\mathbb {C}\) there do exist auxiliary polynomials that have the required boundedness properties. This is in contrast to the situation for polynomials constructed from the monomial lattice. In Theorem 9, we exhibit, for any disk, an explicit construction of such a polynomial. However, since this polynomial is constructed with \(j = 0\) in (9), it tells us nothing about the solution to the inputs to Coppersmith’s theorem.

Theorem 11 shows that even if one manages to find an auxiliary polynomial in the lattice given by (9) that does give nontrivial information about the solutions to the inputs to Coppersmith’s theorem, this polynomial will still not be useful. Either this polynomial must have degree so large that the root-finding step does not run in polynomial time, or N must have a small prime factor. For this reason, for N that has only large prime factors, using auxiliary polynomials constructed using binomial polynomials will not lead to an improvement in the \(N^{1/d}\) bound in Coppersmith’s method.

Theorem 9

(Existence of Bounded Binomial Polynomials). Suppose \(\delta \) is any positive real number. Suppose \(c > 1\). For all sufficiently large integers N, there is a non-zero polynomial of the form

$$\begin{aligned} h(x) = \sum _{0 \le i \le c N^{\delta }} a_{i} \ b_i(x) \end{aligned}$$
(10)

with \(a_i \in \mathbb {Z}\) such that \(|h(z)| < 1\) for all z in the complex disk \(\{z \in \mathbb {C}: |z| \le N^{\delta } \}\).

Theorem 10

(Explicit Construction for Theorem 9 ). Let \(q_0\) be the unique positive real number such that

$$\begin{aligned} 4 \mathrm {arctan}(q_0/2) = q_0\left( 2\ln (2) - \ln \left( \frac{4}{q_0^2} + 1\right) \right) \end{aligned}$$
(11)

Suppose \(c > q_0 = 3.80572...\), then one can exhibit an explicit h(x) of the kind in ( 9 ) in the following way. Choose any constant \(c'\) with \(q_0< c' < c\). Then for sufficiently large N and all integers t in the range \(c' N^\delta /2 < t \le c N^\delta /2 -1/2\), the function

$$h(x) = b_{2t+1}(x + t)$$

will have the properties in (i).

Theorem 11

(Negative Coppersmith Theorem for Binomial Polynomials). Suppose \(\epsilon > 0\) and that M and N are positive integers. Suppose further that

$$\begin{aligned} N^\epsilon > \prod _{p \le M} p^{1/(p-1)} \end{aligned}$$
(12)

where the product is over the primes p less than or equal to M. This condition holds, for example, if \(1.48774 N^\epsilon \ge M \ge 319\). If there is a non-zero polynomial h(x) of the form

$$\begin{aligned} h(x) = \sum _{0 \le i,j \le M} a_{i,j} \ b_i(x) \ b_j(f(x)/N) \end{aligned}$$
(13)

with \(a_{i,j} \in \mathbb {Z}\) such that \(|h(z)| < 1\) for z in the complex disk \(\{z \in \mathbb {C}: |z| \le N^{(1/d)+ \epsilon } \}\), then N must have a prime factor less than M.

4.1 Proof of Theorems 9 and 10

The proof of Theorem 9 comes in several parts. We first use capacity theory to show that non-zero polynomials of the desired kind exist. This argument does not give any information about the degree of the polynomials, however. So we then use an explicit geometry of numbers argument to show the existence of a non-zero polynomial of a certain bounded degree which is of the desired type. Finally, we give an explicit construction of an h(x). This h(x) has a somewhat larger degree than the degree which the geometry of numbers argument shows can be achieved. It would be interesting to see if the LLL algorithm would lead to a polynomial time method for constructing a lower degree polynomial than the explicit construction.

In this section we assume the notations of Theorem 9. The criterion that h(x) be a polynomial of the form

$$h(x) = \sum _i a_i b_i(x)$$

with \(a_i \in \mathbb {Z}\) is an extrinsic property, which will be discussed in more detail in Step 1 of Sect. 5.1. In short, this extrinsic property arises because h(x) must have a particular form. We need to convert this to an intrinsic criterion, in this case observing that these polynomials take \(\mathbb {Z}_p\) to \(\mathbb {Z}_p\). The key to doing so is the following result of Polya:

Theorem 12

(Polya). The set of polynomials \(h(x) \in \mathbb {Q}[x]\) which have integral values on every rational integer \(r \in \mathbb {Z}\) is exactly the set of integral combinations \(\sum _i a_i b_i(x)\) of binomial polynomials \(b_i(x)\).

Corollary 1

The set of polynomials \(h(x) \in \mathbb {Q}[x]\) which are integral combinations \(\sum _i a_i b_i(x)\) of binomial polynomials \(b_i(x)\) is exactly the set of h(x) such that \(|h(z)|_p \le 1\) for all \(z \in \mathbb {Z}_p\) and all primes p.

The corollary follows because \(\mathbb {Z}\) is dense in \(\mathbb {Z}_p\).

Our main goal in the proof of Theorem 9 is to show there are \(h(x) \ne 0\) as in Corollary 1 such that \(|h(z)| < 1\) for z in the complex disk \(E_\infty = \{z \in \mathbb {C}: |z| \le N^\delta \}\). We break reaching this goal into steps.

Applying Capacity Theory Directly. In view of Corollary 1, the natural adelic set to consider would be

$$\begin{aligned} \mathbb {E} = \prod _p E_p \times E_\infty \quad \mathrm {with} \quad E_p = \mathbb {Z}_p \quad \mathrm {for \ all } \quad p \end{aligned}$$
(14)

However, this choice does not meet the criteria for \(\gamma (\mathbb {E})\) to be well defined, because it is not true that \(E_p = \overline{\mathbb {Z}}_p\) for all but finitely many p. However, for all \(Y \ge 2\), the adelic set

$$\begin{aligned} \mathbb {E}' = \prod _{p \le Y} \mathbb {Z}_p \times \prod _{p > Y} \overline{\mathbb {Z}}_p \times E_\infty \end{aligned}$$
(15)

does satisfy the criteria for \(\gamma (\mathbb {E})\) to be well defined. One has

$$\gamma _p(\mathbb {Z}_p) = p^{-1/(p-1)},\quad \gamma _p(\overline{\mathbb {Z}}_p) = 1 \quad \mathrm {and} \quad \gamma _\infty (E_\infty ) = N^\delta .$$

So

$$\begin{aligned} \ln \gamma (\mathbb {E}') = \ln \left( \prod _{p\le Y} \gamma _p(\mathbb {Z}_p) \times \gamma _\infty (E_\infty ) \right) = -\sum _{p \le Y} \frac{\ln (p)}{p-1} + \ln (N^\delta ) \end{aligned}$$
(16)

Here as \(Y \rightarrow \infty \), the quantity \(-\sum _{p \le Y} \frac{\ln (p)}{p-1}\) diverges to \(-\infty \). So for all sufficiently large Y we have \(\gamma (\mathbb {E}') < 1\). We then find as before that Cantor’s work produces a non-zero polynomial \(h(x) \in \mathbb {Q}[x]\) such that for all v and all elements z of the v-component of \(\mathbb {E}'\) one has \(|h(z)|_v \le 1\), with \(|h(z)| < 1\) if \(v = \infty \). In particular, \(|h(z)|_p \le 1\) for all primes p and all \(z \in \mathbb {Z}_p \subset \overline{\mathbb {Z}}_p\). So Corollary 1 shows h(x) is an integral combination of binomial polynomials such that \(|h(z)| < 1\) if \(z \in \mathbb {C}\) and \(|z| \le N^\delta \).

Using the Geometry of Numbers to Control the Degree of Auxiliary Polynomials. Minkowski’s theorem says that if L is a lattice in a Euclidean space \(\mathbb {R}^n\) and C is a convex symmetric subset of \(\mathbb {R}^n\) of volume at least equal to \(2^n\) times the generalized index \([L:\mathbb {Z}^n]\), there must be a non-zero element of \(L \cap C\). To apply this to construct auxiliary polynomials, one takes C to correspond to a suitably bounded set of polynomials with real coefficients, and L to correspond to those polynomials with rational coefficients of the kind one is trying to construct.

In the case at hand, suppose \(1 \le r \in \mathbb {R}\). Let \(\mathbb {Z}[x]_{\le r}\) be the set of integral polynomials of degree \(\le r\), and let \(L_{\le r}\) be the \(\mathbb {Z}\)-span of \(\{b_i(x): 0 \le i \le r, i \in \mathbb {Z}\}\). To show the first statement of Theorem 9, it will suffice to show that if \(c > 1\), then for sufficiently large \(r = N^\delta > 0\), there is a non-zero \(f(x) \in L_{\le cr}\) such that \(|f(z)| < 1\) for \(z \in \mathbb {C}\) such that \(|z| \le r\).

Let \(m = \lfloor cr \rfloor \) be the largest integer less than or equal to cr. By considering leading coefficients, we have

$$\ln [L_{\le m} : \mathbb {Z}[x]_{\le m}] = \ln \prod _{i = 0}^m i! = m^2 \ln (m)/2 \cdot (1 + o(1))$$

where \(o(1) \rightarrow 0\) as \(m \rightarrow \infty \). Let C be the set of polynomials with real coefficients of the form

$$\sum _{i = 0}^m q_i (x/r)^i \quad \mathrm {with}\quad |q_i| \le 1/(m+2).$$

We consider C as a convex symmetric subset of \(\mathbb {R}^{m+1}\) by mapping a polynomial to its vector of coefficients. Then

$$\ln \mathrm {vol}(C) = (m+1)\cdot (\ln (2) - \ln (m+2)) - \sum _{i = 0}^m i \ln (r) = -\ln (r) m^2/2 \cdot (1 + o(1)).$$

Since \(\mathbb {Z}[x]_{\le m}\) maps to a lattice in \(\mathbb {R}^{m+1}\) with covolume 1, we find

$$\begin{aligned} {\small \ln \mathrm {vol}(C) - \ln \mathrm {vol}(\mathbb {R}^{m+1}/L_{\le m}) \ge (\ln (m) - \ln (r)) m^2/2 \cdot (1 + o(1)) = \ln (c) \cdot m^2/2 \cdot (1 + o(1)).} \end{aligned}$$

Since \(\ln (c) > 0\), for sufficiently large m, the right hand side is greater than \(2 \ln (m+1)\). Hence Minkowski’s Theorem produces a non-zero \(f(x) \in L_{\le m}\) in C. One has

$$|f(z)| \le \sum _{i = 0}^m |z/r|^i/(m+2) < 1$$

if \(z \in \mathbb {C}\) and \(|z| < r\), so we have proved Theorem 9.

An Explicit Construction. Theorem 10 concerns the polynomials \(b_{2t+1}(x+t)\) when \(t > 0\) is an integer. This polynomial takes integral values at integral x, so it is an integral combination of the polynomials \(b_i(x)\) with \(0 \le i \le 2t+1\) by Polya’s Theorem 12. To finish the proof of Theorem 10, it will suffice to show the following. Let \(q_0\) be the unique positive solution of the Eq. (11), and suppose \(q > q_0\). Let D(r) be the closed disk \(D(r) = \{z \in \mathbb {C}:|z| \le r\}\). We will show that if r is sufficiently large, then

$$\begin{aligned} |b_{2t+1}(z+t)| < 1\quad \mathrm {if} \quad 2t \ge q r\quad \mathrm {and} \quad z \in D(r). \end{aligned}$$
(17)

We have

$$b_{2t+1}(z + t) = \frac{\prod _{j = 0}^{2t} (z+t - j)}{(2t+1)!} = \frac{\prod _{j = -t}^{t} (z - j)}{(2t+1)!} = \pm \frac{z \cdot \prod _{j = 1}^t (z^2 - j^2)}{(2t+1)!}$$

For \(j \ge 0\) and \(z \in D(r)\) we have

$$|-r^2 - j^2| = r^2 + j^2 \ge |z^2 - j^2|.$$

So

$$\mathrm {sup}(\{b_{2t+t}(z+t): z \in D(r)\}) = \frac{r \cdot \prod _{j = 1}^t (r^2 + j^2)}{(2t+1)!}.$$

Taking logarithms gives

$$\begin{aligned} \ln {\mathrm {sup} (\{b_{2t+t}(z+t): z \in D(r)\}) =\ln (r) + \sum _{j = 1}^t \ln (r^2 + j^2) - \ln ((2t+1)!)}. \end{aligned}$$
(18)

We now suppose \(t \ge r\), so \(\xi = r/t \le 1\). Then

$$\begin{aligned} \sum _{j = 1}^t \ln (r^2 + j^2)= & {} t \ln (t^2) + t \cdot \frac{1}{t} \sum _{j = 1}^t \ln (\xi ^2 + (j/t)^2)\nonumber \\= & {} 2t \ln (t) + t \cdot \int _0^1 \ln (\xi ^2 + s^2) ds + o(t) \end{aligned}$$
(19)

as \(t \rightarrow \infty \). By integration by parts,

$$\begin{aligned} \int \ln (\xi ^2 + s^2) ds = s \ln (\xi ^2 + s^2) - 2s + 2\xi \mathrm {arctan}(s/\xi ). \end{aligned}$$
(20)

By Stirling’s formula,

$$\begin{aligned} \ln ((2t+1)!) = (2t+1)\ln (2t+1)\,-\,(2t + 1)\,+\,o(t) = 2t \ln (t)\,+\,2t \ln (2)\,-\,2t\,+\,o(t). \end{aligned}$$
(21)

Since \(\ln (r) = o(t)\), we get from (18), (20) and (21) that

$$\begin{aligned} \ln (\mathrm {sup} \{b_{2t+t}(z+t): z \in D(r)\}) = t \cdot (\ln (\xi ^2 + 1)\,+\,2\xi \mathrm {arctan}(\xi ^{-1})\,-\,2\ln (2))\,+\,o(t). \end{aligned}$$
(22)

Writing \(q = 2t/r = 2/ \xi \ge 2\) and multiplying both sides of (22) by \(q > 0\), we see that if

$$f(q) = q\ln \left( \frac{4}{q^2} + 1 \right) + 4 \mathrm {arctan}(q/2) - 2\ln (2) q < 0$$

then for sufficiently large t the supremum on the left in (18) is negative and we have the desired bound. Here from \(q \ge 2\) we have

$$f'(q) =\ln (1/q^2 + 1/4) \le \ln (1/2)< 0 < f(2) \quad \mathrm {and}\quad \lim _{q \rightarrow +\infty } f(q) = -\infty .$$

So there is a unique positive real number \(q_0\) with \(f(q_0) = 0\), and \(f(q) < 0\) for \(q > q_0\). This establishes (17) and finishes the proof of part (ii) of Theorem 9.

4.2 Proof of Theorem 11

The proof of Theorem 11 uses a feedback procedure. The feedback in this case is that if N has no small prime factor p, then for all small primes p we can increase the set \(E_p\). This is described in more detail in Sect. 5.2.

Let M be a positive integer and suppose \(\epsilon > 0\). Suppose that there is a polynomial of the form

$$\begin{aligned} h(x) = \sum _{0 \le i,j \le M } a_{i,j} b_i(x) b_j(f(x)/N) \end{aligned}$$
(23)

such that \(a_{i,j} \in \mathbb {Z}\) and \(|h(z)| < 1\) for all \(z \in \mathbb {C}\) such that \(|z| \le N^{1/d + \epsilon }\). We show that if M satisfies one of the inequalities involving N in the statement of Theorem 11, then N must have a prime divisor bounded above by M. We will argue by contradiction. Thus we need to show that the following hypothesis cannot hold:

Hypothesis 1

No prime \(p \le M\) divides N, and either (12) holds or \(1.48774 N^\epsilon \ge M \ge 319\).

The point of the proof is to show that Hypothesis 1 leads to h(x) having small sup norms on all components of an adelic set \(\mathbb {E}\) which has capacity larger than 1. The reason that the hypothesis that no prime \(p \le M\) divides N enters into the argument is that this guarantees that f(z)/N will lie in the p-adic integers \(\mathbb {Z}_p\) for all \(z \in \mathbb {Z}_p\) when \(p \le M\). This will lead to being able to take the component of \(\mathbb {E}\) at such p to be \(\mathbb {Z}_p\). The p-adic capacity of \(\mathbb {Z}_p\) is \(p^{-1/(p-1)}\), as noted in Fact 7. This turns out to be relatively large when one applies various results from analytic number theory to get lower bounds on capacities.

To start a more detailed proof, let p be a prime and suppose \(0 \le i, j \le M\).

Lemma 1

If \(p \le M\) set \(E_p = \mathbb {Z}_p\). Then \(|h(z)|_p \le 1\) if \(z \in E_p\) and the capacity \(\gamma _p(E_p)\) equals \(p^{-1/(p-1)} |N|_p\).

Proof

If \(p \le M\) and \(x \in \mathbb {Z}_p\), then \(b_i(x) \in \mathbb {Z}_p\) since \(\mathbb {Z}\) is dense in \(\mathbb {Z}_p\) and \(b_i(x) \in \mathbb {Z}\) for all \(x \in \mathbb {Z}\). Furthermore, \(f(x)/N \in \mathbb {Z}_p\) for \(x \in \mathbb {Z}_p\) since we have assumed N is prime to p and \(f(x) \in \mathbb {Z}[x]\). Therefore \(b_j(f(x)/N) \in \mathbb {Z}_p\) for all j. Since the coefficients \(a_{i,j}\) in (23) are integers, we conclude \(|h(z)|_p \le 1\). We remarked earlier in Fact 7 that \(\gamma _p(\mathbb {Z}_p) = p^{-1/(p-1)}\). Since \(p \le M\), we have supposed that p does not divide N. So \(|N|_p = 1\), and we get \(\gamma _p(E_p) = \gamma (\mathbb {Z}_p) = p^{-1/(p-1)} |N|_p\).

Lemma 2

If \(p > M\) set \(E_p =f^{-1}(N\overline{\mathbb {Z}}_p)\). Then \(|h(z)|_p \le 1\) if \(z \in E_p\) and \(\gamma _p(E_p) = |N|_p^{-1/p}\).

Proof

We first note that \(0 \le i, j \le M < p \) implies that \(|i!|_p = |j!|_p = 1\). Recall that \(\overline{\mathbb {Z}}_p = \{x \in \overline{\mathbb {Q}}_p: |x|_p \le 1\}\). If \(x \in f^{-1}(N \overline{\mathbb {Z}}_p)\) then \(x \in \overline{\mathbb {Z}}_p\) since f(x) is monic with integral coefficients. So

$$|b_i(x)|_p = \frac{|x\cdot (x-1) \cdots (x - i +1)|_p}{|i!|_p} \le 1$$

and

$$ |b_j(f(x)/N)|_p = \frac{|f(x)/N\cdot (f(x)/N-1) \cdots (f(x)/N - j +1)|_p}{|j!|_p} \le 1 $$

since \(x - k\) and \( f(x)/N - k\) lie in \( \overline{\mathbb {Z}}_p\) for all integers k and \(|i!|_p = |j!|_p = 1\). Because the \(a_{i,j}\) in (2) are integral, we conclude \(|h(z)|_p \le 1\) if \(z \in E_p =f^{-1}(N\overline{\mathbb {Z}}_p)\). The capacity \(\gamma _p(E_p)\) is \(|N|_p^{-1/p}\) by Fact 8.

Lemma 3

Set \(E_\infty = \{z \in \mathbb {C}: |z| \le N^{1/d + \epsilon } \}\). Then \(|h(z)|_\infty < 1\) if \(z \in E_\infty \) and \(\gamma _\infty (E_\infty ) = N^{1/d + \epsilon }\).

Proof

This first statement was one of our hypotheses on h(x), while \(\gamma _\infty (E_\infty ) = N^{1/d + \epsilon }\) by Fact 7.

We conclude from these Lemmas and Fact 9 that when

$$\begin{aligned} \mathbb {E} = \prod _p E_p \times E_\infty \end{aligned}$$

we have

$$\begin{aligned} \gamma (\mathbb {E}) = \left( \prod _{p \le M} p^{-1/(p-1)}\right) \times \left( \prod _{all \ p} |N|_p^{1/d}\right) \times N^{1/d + \epsilon } = \left( \prod _{p \le M} p^{-1/(p-1)}\right) N^\epsilon . \end{aligned}$$
(24)

Here

$$\ln \left( \prod _{p \le M} p^{-1/(p-1)}\right) = - \sum _{p \le M} \frac{ \ln (p)}{p-1}$$

and it follows from [RS62, Theorem 6, p. 70] that if \(M \ge 319\) then

$$\begin{aligned} -\sum _{p \le M} \frac{ \ln (p)}{p-1}= & {} -\sum _{p \le M} \frac{\ln (p)}{p} - \sum _{p \le M} \frac{\ln (p)}{p(p-1)} \nonumber \\\ge & {} -\sum _{p \le M} \frac{\ln (p)}{p} - \sum _p \sum _{n=2}^\infty \frac{\ln (p)}{p^n}\nonumber \\\ge & {} - \ln (M) + \gamma - \frac{1}{\ln (M)} \end{aligned}$$
(25)

where \(\gamma = 0.57721...\) is Euler’s constant.

Hence (24) gives

$$\begin{aligned} \ln (\gamma (\mathbb {E})) = -\sum _{p \le M} \frac{ \ln (p)}{p-1} + \epsilon \ln (N) \ge - \ln (M) + \gamma - \frac{1}{\ln (M)} + \epsilon \ln (N). \end{aligned}$$
(26)

The right hand side is positive if

$$\begin{aligned} N^\epsilon \cdot e^{\gamma - 1/\ln (M)} > M. \end{aligned}$$
(27)

Since we assumed \(M \ge 319\), we have \(e^{\gamma - 1/\ln (M)} \ge 1.497445...\) and so (27) will hold if

$$\begin{aligned} 1.48744 \cdot N^\epsilon > M \end{aligned}$$
(28)

In any case, if the left hand side of (26) is positive then \(\gamma (\mathbb {E}) > 1\). However, we have shown that h(x) is a non-zero polynomial in \(\mathbb {Q}[x]\) such that \(|h(x)|_v \le 1\) for all v when \(x \in E_v\) with strict inequality when \(v = \infty \). By Cantor’s Theorem 7, such an h(x) cannot exist because \(\gamma (\mathbb {E}) > 1\). The contradiction shows that Hypothesis 1 cannot hold, and this completes the proof of Theorem 11.

5 A Field Guide for Capacity-Theoretic Arguments

The proofs in Sects. 3 and 4 illustrate how capacity theory can be used to show the nonexistence and existence of polynomials with certain properties. This paper is a first step toward building a more general framework to apply capacity theory to cryptographic applications. In this section, we step back and summarize how capacity theory can be used in general to show either that auxiliary polynomials with various desirable properties do or do not exist.

The procedure for applying capacity theory to such problems allows for feedback between the type of polynomials one seeks and the computation of the relevant associated capacities. If it turns out that the capacity theoretic computations are not sufficient for a definite conclusion, they may suggest additional hypotheses either on the polynomials or on auxiliary parameters which would be useful to add in order to arrive at a definitive answer. They may also suggest some alternative proof methods which will succeed even when capacity theory used as a black box does not.

5.1 Showing Auxiliary Polynomials Exist

To use capacity theory to show that polynomials \(h(x) \in \mathbb {Q}[x]\) with certain properties exist, one can follow these steps:

  • Step 1. State the conditions on h(x) which one would like to achieve. These can be of an intrinsic or an extrinsic nature.

    1. (a)

      Intrinsic conditions have the following form:

      1. (i)

        For each prime p, one should give a subset \(E_p\) of \(\overline{\mathbb {Q}}_p\). For all but finitely many p, \(E_p\) must be the set \(\overline{\mathbb {Z}}_p\).

      2. (ii)

        One should give a subset \(E_\infty \) of \(\mathbb {C}\).

      3. (iii)

        The set of polynomials \(h(x) \in \mathbb {Q}[x]\) one seeks are all polynomials such that \(|h(z)|_p \le 1\) for all primes p and all \(z \in E_p\) and \(|h(w)| < 1\) if \(w \in E_\infty \).

    2. (b)

      To state conditions on h(x) extrinsically, one writes down the type of polynomial expressions one allows. For example, one might require h(x) to be an integral combination of integer multiples of specified polynomials, e.g. monomials in x as in Theorem 6. Suppose one uses such an extrinsic description, and one is trying to show the existence of h(x) of this form using capacity theory. It is then necessary to come up with an intrinsic description of the above kind with the property that any h(x) meeting the intrinsic conditions must have the required extrinsic description. We saw another example of this in Sect. 4 on binomial polynomials; see also Step 5 below.

  • Step 2. Suppose we have stated an intrinsic condition on h(x) as in parts (i), (ii) and (iii) of Step 1(a). One then needs to check that the adelic set \(\mathbb {E} = \prod _p E_p \times E_\infty \) satisfies certain standard hypotheses specified in [Can80, Rum89, Rum13]. These ensure that the capacity

    $$\begin{aligned} \gamma (\mathbb {E}) = \prod _p \gamma _p(E_p) \cdot \gamma _\infty (E_\infty ) \end{aligned}$$
    (29)

    is well defined. One then needs to employ [Can80, Rum89, Rum13] to find an upper bounds the \(\gamma _p(E_p)\), on \(\gamma _\infty (E_\infty )\) and then on \(\gamma (\mathbb {E})\). This may also require results from analytic number theory concerning the distribution of primes. When using this method theoretically, there may be an issue concerning the computational complexity of finding such upper bounds. However, if \(E_p\) and \(E_\infty \) have a simple form (e.g. if they are disks), explicit formulas are available. Notice that the requirement in part (i) of Step 1 that \(E_p = \overline{\mathbb {Z}}_p\) for all but finitely many p forces \(\gamma _p(E_p) = 1\) for all but finitely many p. So the product on the right side of (29) is well defined as long as \(\gamma _\infty (E_\infty )\) and \(\gamma _p(E_p)\) are for all p.

  • Step 3. If the computation in Step 2 shows \(\gamma (\mathbb {E}) < 1\), capacity theory guarantees that there is some non-zero polynomial \(h(x) \in \mathbb {Q}[x]\) which satisfies the bounds in part (iii) of Step 1. However, one has no information at this point about the degree of h(x).

  • Step 4. Suppose that Step 2 shows \(\gamma (\mathbb {E}) < 1\) and that we want to show there is an h(x) as in Step 3 satisfying a certain bound on its degree. There are three levels of looking for such degree bounds.

    1. a.

      The most constructive method is to present an explicit construction of an h(x) which one can show works. We did this in the previous section in the case of integral combinations of binomial polynomials.

    2. b.

      The second most constructive method is to convert the existence of h(x) into the problem of finding a short vector in a suitable lattice of polynomials and to apply the LLL algorithm. One needs to show that the LLL criteria are met once one considers polynomials of a sufficiently large degree, and that a short vector will meet the intrinsic criteria on h(x). We will return in later papers to the general question of when \(\gamma (\mathbb {E}) < 1\) implies that there is a short vector problem whose solution via LLL will meet the intrinsic criteria. This need not always be the case. The reason is that in the geometry of numbers, one can find large complicated convex symmetric sets which are very far from being generalized ellipsoids. However, in practice, the statement that \(\gamma (\mathbb {E}) < 1\) makes it highly likely that the above LLL approach will succeed.

    3. c.

      Because of the definition of sectional capacity in [Chi91, RLV00], the following approach is guaranteed to succeed by \(\gamma (\mathbb {E}) < 1\). Minkowski’s Theorem in the geometry of numbers will produce (in a non-explicit manner) a polynomial h(x) of large degree m which meets the intrinsic criteria. One can estimate how large m must be by computing certain volumes and generalized indices. We illustrate such computations in Sect. 4 in the case of intrinsic conditions satisfied by integral combination of binomial polynomials.

  • Step 5. It can happen that the most natural choices for \(E_p\) and \(E_\infty \) in step 1 above do not satisfy all the criteria for the capacity of \(\mathbb {E} = \prod _p E_p \times E_\infty \) to be well defined. One can then adjust these choices slightly. To obtain more control on the degrees of auxiliary functions, one can try an explicit Minkowski argument of the kind use in the proof of the positive result concerning integral combinations of binomial polynomials in Theorem 9 above.

5.2 Showing Auxiliary Polynomials Do Not Exist

To use capacity theory to show that polynomials \(h(x) \in \mathbb {Q}[x]\) with certain properties do not exist, one can follow these steps:

  • Step 1. Specify the set of properties you want h(x) to have. Then show that the following is true for every h(x) with these properties:

    1. (i)

      For each prime p, exhibit a set \(E_p\) of \(\overline{\mathbb {Q}}_p\) such that \(|h(z)|_p \le 1 \) if \(z \in E_p\).

      For all but finitely many p, \(E_p\) must be the set \(\overline{\mathbb {Z}}_p\).

    2. (ii)

      Exhibit a closed subset \(E_\infty \) of \(\mathbb {C}\) such that \(|h(z)| < 1\) if \(z \in E_\infty \).

      It is important that \(h(x)\in \mathbb {Q}[x]\) with the desired properties meet the criteria in (i) and (ii).

  • Step 2. As before, one needs to check that the adelic set \(\mathbb {E} = \prod _p E_p \times E_\infty \) satisfies certain standard hypotheses specified in [Can80, Rum89, Rum13]. These ensure that the capacity

    $$\begin{aligned} \gamma (\mathbb {E}) = \prod _p \gamma _p(E_p) \cdot \gamma _\infty (E_\infty ) \end{aligned}$$
    (30)

    is well defined. One then needs to find a lower bound on \(\gamma (\mathbb {E})\) using lower bounds on the \(\gamma _p(E_p)\) and on \(\gamma _\infty (E_\infty )\). One may also require information from analytic number theory, e.g. on the distributions of prime numbers less than a given bound.

  • Step 3. If the computation in Step 2 shows \(\gamma (\mathbb {E}) > 1\), capacity theory guarantees that there is no non-zero polynomial \(h(x) \in \mathbb {Q}[x]\) which satisfies the intrinsic conditions (i) and (ii) of Step 1. This means there do not exist of polynomials h(x) having the original list of properties.

  • Step 4. Suppose that in Step 3, we cannot show \(\gamma (\mathbb {E}) > 1\) due to the fact that the sets \(E_p\) and \(E_\infty \) in Step 1 are not sufficient large. One can now change the original criteria on h(x), or take into account some additional information, to try to enlarge the sets \(E_p\) and \(E_\infty \) for which Step 1 applies. We saw in the previous section how this procedure works in the case of integral combinations of certain products of binomial polynomials. For example, if one assumes that certain other parameters (e.g. the modulus of a congruence) have no small prime factors, one can enlarge the sets \(E_p\) in Step 1 which are associated to small primes.

6 Conclusion

In this work, we drew a new connection between two disparate research areas: lattice-based techniques for cryptanalysis and capacity theory. This connection has benefits for researchers in both areas.

  • Capacity Theory for cryptographers: We have shown that techniques from capacity theory can be used to show that the bound obtained by Coppersmith’s method in the case of univariate polynomials is optimal and the best available class of techniques for solving these types of problems cannot be extended. This has implications for cryptanalysis, and the tightness of cryptographic security reductions.

  • Cryptography for capacity theorists: Capacity theory provides a method for calculating the conditions under which certain auxiliary polynomials exist. Coppersmith’s method provides an efficient algorithm for finding these auxiliary polynomials. Until this time, capacity theory has not addressed the computational complexity actually producing auxiliary functions.

We used capacity theory to answer three questions of Coppersmith in [Cop01]

  1. 1.

    Can the exponent 1/d be improved (possibly through improved lattice reduction techniques)? No, the desired auxiliary polynomial simply does not exist.

  2. 2.

    Does restricting attention to the real line \([-N^{-1/d},N^{1/d}]\) instead of the complex disk \(|z| \le N^{1/d}\) improve the situation? No.

  3. 3.

    Does considering lattices based on binomial polynomials improve the situation? No, these lattices have the desired auxiliary polynomials, but for RSA moduli, their degree is too large to be useful.

Since Coppersmith’s method is one of the primary tools in asymmetric cryptanalysis, these results give an indication of the security of many factoring-based cryptosystems.

This paper lays a foundation for several directions of future work. Coppersmith’s study of small integral solutions of equations in two variables and bivariate equations modulo N [Cop97] is related to capacity theory on curves, as developed by Rumely in [Rum89, Rum13]. The extension of Coppersmith’s method to multivariate equations [JM06, Jut98] is connected to capacity theory on higher dimensional varieties, as developed in [Chi91, RLV00, CMBPT15]. Multivariate problems raise deep problems in arithmetic geometry about the existence of finite morphisms to projective spaces which are bounded on specified archimedean and non-archimedean sets. Interestingly, Howgrave-Graham’s extension of Coppersmith’s method to find small roots of modular equations modulo unknown moduli [HG01, May10] appears to pertain to joint capacities of many adelic sets, a topic which has not been developed to our knowledge in the capacity theory literature. It is an intriguing question whether capacity theory can be extended to help us understand the limitations of these more general variants of Coppersmith’s method.