Abstract
In Sect. 4.1, as a preliminary to the discussion of scaling theory, we gave a general heuristic treatment of the geometry of phase transitions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See Definition 17.1.1.
- 2.
- 3.
See Fig. 4.2c, where the points representing coexistent phases are denoted by A and B.
- 4.
For an account of this work see Rowlinson (1969).
- 5.
The reader is recommended to refer to this example as an illustration of the development of Landau theory with one order parameter.
- 6.
Ignore for the moment the shaded regions. Remember also that isotherms for the van der Waals equation will be mirror images about a vertical line of those given in Fig. 5.1a, because increase in pressure yields a decrease in \(v\): see the comment in the footnote on p. 6.
- 7.
Although
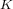 increases along the first-order transition curve it is not necessarily the case that
increases along the first-order transition curve it is not necessarily the case that  does. However, this will be assumed in line with Fig. 4.7.
does. However, this will be assumed in line with Fig. 4.7. - 8.
Thus, contrary to the common belief, diamonds are not ‘for ever’, just for a very long time.
- 9.
For a translation see Rowlinson (1988) and for an assessment of the legacy of van der Waals see Rowlinson (1973).
- 10.
In fact, in terms of the variables introduced in Sect. 1.1, exactly equal to \(M\).
- 11.
By taking the perfect gas \(v\rightarrow \infty \) limit, when the entropy is given by the Sackur-Tetrode equation, it can be shown (Lavis and Bell 1977) that
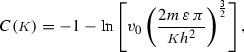
where \(m\) is the mass of a particle and \(h\) is Planck’s constant.
- 12.
Order parameters are often given a vector form, the case of two order parameters being referred to as that of a two-dimensional order parameter.
- 13.
- 14.
And, of course, the same question can be posed in relation the neighbourhood of other critical regions.
- 15.
In both the statistical mechanical and catastrophe sense (Definition 17.1.11 together with the footnote).
- 16.
We have explicitly displayed only those coefficients needed in the calculations of the asymptotic forms for the response functions.
- 17.
Sometimes referred to as the mean-field or Landau values.
- 18.
The leading factor of \(2/\sqrt{3}\) in \(p\) is included in order to make the matrix representations of
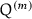 and
and  unitary. It is omitted in series calculations (see Enting and Wu 1982, and Sect. 14.2.1).
unitary. It is omitted in series calculations (see Enting and Wu 1982, and Sect. 14.2.1). - 19.
\(\mathcal {S}_3\) is isomorphic to the dihedral group \(\mathcal {D}_3\) and to \(\mathcal {C}_{3{{\text {v}}}}\) (see the character table in Example 17.3.2).
- 20.
The free-energy density (5.5.3) is, therefore, the universal unfolding of
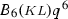 at the tricritical point.
at the tricritical point. - 21.
It is clear that \((\Theta _2^{(\mathrm {t})}\Theta _3^{(\mathrm {t})})\) are the coordinates \((\Theta _2,\varTheta _3)\) defined in (4.6.14) with \(a=a_\mathrm {t}\). It is for this reason that we have retained the labels 2,3 rather that the more obvious 1,2.
- 22.
On \({\mathcal {C}}\),
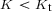 , and, on \({\mathcal {T}}\),
, and, on \({\mathcal {T}}\), 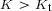 (Fig. 4.10).
(Fig. 4.10). - 23.
For the heat capacity exponents we should need also to assume an asymptotic form for
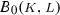 as we did for the critical point in (5.3.22).
as we did for the critical point in (5.3.22). - 24.
Suppose, in the case \(n=1\), we select the form of \(\sigma \) which minimizes \({\hat{\phi }}_1^{({{\text {C}}}{{\text {L}}})}\). For
 this will occur when \(\sigma \) is uniform and equal to \(m\) over \({\mathcal {V}}\) and, assuming that this distribution dominates the functional integral in (5.6.4) we recover (5.3.32).
this will occur when \(\sigma \) is uniform and equal to \(m\) over \({\mathcal {V}}\) and, assuming that this distribution dominates the functional integral in (5.6.4) we recover (5.3.32). - 25.
Not to be confused with the derivatives of the free-energy density appearing in other chapters.
- 26.
- 27.
In this case \({\mathfrak {d}}=d\), the thermodynamic limit is taken in each of the \(d\) dimensions.
- 28.
The discussion presented here is not quite complete. As pointed out in Sect. 4.8 it is necessary to consider other approaches to the critical point to determine whether the change of effective dimension can be consistently applied. This involves consideration of the case \(\theta _1 \ne 0\), when the magnetization is given, as in Sect. 6.1, by a root of a cubic equation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Lavis, D.A. (2015). Phenomenological Theory and Landau Expansions. In: Equilibrium Statistical Mechanics of Lattice Models. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9430-5_5
Download citation
DOI: https://doi.org/10.1007/978-94-017-9430-5_5
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9429-9
Online ISBN: 978-94-017-9430-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


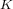 increases along the first-order transition curve it is not necessarily the case that
increases along the first-order transition curve it is not necessarily the case that  does. However, this will be assumed in line with Fig.
does. However, this will be assumed in line with Fig. 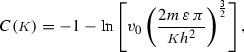
 are not functions of
are not functions of  for
for  appears in
appears in  only in a term linear in
only in a term linear in  ; see (
; see ( and
and  unitary. It is omitted in series calculations (see Enting and Wu 1982, and Sect. 14.2.1).
unitary. It is omitted in series calculations (see Enting and Wu 1982, and Sect. 14.2.1). at the tricritical point.
at the tricritical point. , and, on
, and, on 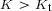 (Fig.
(Fig. 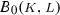 as we did for the critical point in (
as we did for the critical point in ( this will occur when
this will occur when  ,
,  .
.