Abstract
In this chapter we present the notions of communicating, transient and recurrent states, as well as the concept of irreducibility of a Markov chain. We also examine the notions of positive and null recurrence, periodicity, and aperiodicity of such chains. Those topics will be important when analysing the long-run behavior of Markov chains in the next chapter.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In graph theory, one says that
 and
and  are strongly connected.
are strongly connected. - 2.
almost surely.
- 3.
almost surely.
- 4.
For any sequence \((a_n)_{n\ge 0}\) of nonnegative real numbers, \(\displaystyle \sum _{n=0}^\infty a_n < \infty \) implies \(\lim _{n\rightarrow \infty } a_n = 0\).
Author information
Authors and Affiliations
Corresponding author
Exercises
Exercises
Exercise 6.1
Consider a Markov chain \((X_n)_{n\ge 0}\) on the state space \(\{ 0,1,2,3 \}\), with transition matrix
-
(a)
Draw the graph of this chain and find its communicating classes. Is this Markov chain reducible? Why?
-
(b)
Find the periods of states
 ,
,  ,
,  , and
, and  .
. -
(c)
Compute \(\mathbb {P}(T_0<\infty \mid X_0=0)\), \(\mathbb {P}(T_0 = \infty \mid X_0=0)\), and \(\mathbb {P}(R_0<\infty \mid X_0=0)\).
-
(d)
Which state(s) is (are) absorbing, recurrent, and transient?
Exercise 6.2
Consider the Markov chain on \(\{ 0 , 1 , 2 \}\) with transition matrix
-
(a)
Is the chain irreducible? Give its communicating classes.
-
(b)
Which states are absorbing, transient, recurrent, positive recurrent?
-
(c)
Find the period of every state.
Exercise 6.3
Consider a Markov chain \((X_n)_{n\ge 0}\) on the state space \(\{ 0,1,2,3,4\}\), with transition matrix
-
(a)
Draw the graph of this chain.
-
(b)
Find the periods of states
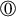 ,
,  ,
,  , and
, and  .
. -
(c)
Which state(s) is (are) absorbing, recurrent, and transient?
-
(d)
Is the Markov chain reducible? Why?
Exercise 6.4
Consider the Markov chain with transition matrix
-
(a)
Is the chain reducible? If yes, find its communicating classes.
-
(b)
Determine the transient and recurrent states of the chain.
-
(c)
Find the period of each state.
Exercise 6.5
Consider the Markov chain with transition matrix
-
(a)
Is the chain irreducible? If not, give its communicating classes.
-
(b)
Find the period of each state. Which states are absorbing, transient, recurrent, positive recurrent?
Exercise 6.6
In the following chain, find:
-
(a)
the communicating class(es),
-
(b)
the transient state(s),
-
(c)
the recurrent state(s),
-
(d)
the positive recurrent state(s),
-
(e)
the period of every state.

Exercise 6.7
Consider two boxes containing a total of N balls. At each unit of time one ball is chosen randomly among N and moved to the other box.
-
(a)
Write down the transition matrix of the Markov chain \((X_n)_{n\in {\mathord {\mathbb N}}}\) with state space \(\{ 0, 1, 2, \ldots , N\}\), representing the number of balls in the first box.
-
(b)
Determine the periodicity, transience and recurrence of the Markov chain.
Exercise 6.8
-
(a)
Is the Markov chain of Exercise 4.10-(a) recurrent? positive recurrent?
-
(b)
Find the periodicity of every state.
-
(c)
Same questions for the success runs Markov chain of Exercise 4.10-(b).
Problem 6.9
Let \(\alpha > 0\) and consider the Markov chain with state space \({\mathord {\mathbb N}}\) and transition matrix given by
and a reflecting barrier at 0, such that \(P_{0,1}=1\). Compute the mean return times \(\mathrm{I}\! \mathrm{E}[ T^r_k \mid X_0 = k ]\) for \(k\in {\mathord {\mathbb N}}\), and show that the chain is positive recurrent if and only if \(\alpha < 1\).
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Privault, N. (2018). Classification of States. In: Understanding Markov Chains. Springer Undergraduate Mathematics Series. Springer, Singapore. https://doi.org/10.1007/978-981-13-0659-4_6
Download citation
DOI: https://doi.org/10.1007/978-981-13-0659-4_6
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-0658-7
Online ISBN: 978-981-13-0659-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 and
and  are strongly connected.
are strongly connected. ,
,  ,
,  , and
, and  .
.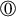 ,
,  ,
,  , and
, and  .
.