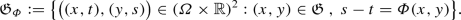Abstract
We study the ergodic theory of horocycle flows on hyperbolic surfaces with infinite genus. In this case, the nontrivial ergodic invariant Radon measures are all infinite. We explain the relation between these measures and the positive eigenfunctions of the Laplacian on the surface. In the special case of \(\mathbb Z^d\)-covers of compact hyperbolic surfaces, we also describe some of their ergodic properties, paying special attention to equidistribution and to generalized laws of large numbers.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The theorem is a consequence of a stronger result by Dani and Smillie on the equidistribution of nonperiodic horocycle orbits on hyperbolic surfaces of finite area. For more on equidistribution, see Sect. 4.
- 2.
Here is how to deduce the ratio ergodic theorem for flows from the ratio ergodic theorem for maps [25]: It is enough to treat the case \(0\le f\in L^1\), \(0\le g\in L^\infty \setminus \{0\}\), because if we know the ratio ergodic theorem for all \(f\in L^1_+, g\in L^\infty _+\) then we know it for all \(f\in L^1, g\in L^1_+\). Let \(S:=T^1\), \(F(x):=\int _0^1 f(T^t x) dt\), and \(G(x):=\int _0^1 g(T^t x) dt\).
$$\begin{aligned}&\left| \frac{\int _0^\tau f\circ T^t dt}{\int _0^\tau g\circ T^t dt}-\frac{\sum _{k=0}^{\lfloor \tau \rfloor } F\circ S^k}{\sum _{k=0}^{\lfloor \tau \rfloor } G\circ S^k}\right| \le \frac{F\circ S^{\lfloor \tau \rfloor }}{\sum _{k=0}^{\lfloor \tau \rfloor -1}G\circ S^k}+\frac{G\circ S^{\lfloor \tau \rfloor }}{\sum _{k=0}^{\lfloor \tau \rfloor -1}G\circ S^k}\\&=\frac{\sum _{k=0}^{\lfloor \tau \rfloor }F\circ S^k}{\sum _{k=0}^{\lfloor \tau \rfloor }G\circ S^k}\cdot \frac{\sum _{k=0}^{\lfloor \tau \rfloor }G\circ S^k}{\sum _{k=0}^{\lfloor \tau \rfloor -1}G\circ S^k}-\frac{\sum _{k=0}^{\lfloor \tau \rfloor -1}F\circ S^k}{\sum _{k=0}^{\lfloor \tau \rfloor -1}G\circ S^k}+\frac{G\circ S^{\lfloor \tau \rfloor }}{\sum _{k=0}^{\lfloor \tau \rfloor -1}G\circ S^k}\xrightarrow [\tau \infty ]{}0\text { a.e.} \end{aligned}$$by the ratio ergodic theorem for S, and since \(\Vert G\Vert _\infty <\infty \) and \(\sum G\circ S^k=\infty \) (conservativity). Thus the existence of \(\lim \frac{\sum _{k=0}^{\lfloor \tau \rfloor } F\circ S^k}{\sum _{k=0}^{\lfloor \tau \rfloor } G\circ S^k}\) (ratio ergodic theorem for maps) implies the existence of \(\lim \frac{\int _0^\tau f\circ T^t dt}{\int _0^\tau g\circ T^t dt}\) (ratio ergodic theorem for flows).
- 3.
The result holds for a larger class of surfaces (“weakly tame surfaces”). See [50].
- 4.
This is less obvious than it looks, because when we modified the cutting sequence at \(Y_{in_0}\), we may have also inadvertently modified the cutting sequences at \(Y_j\) for j close to \(i n_0\). We can deal with the problem by taking \(k_0\) and \(n_0\) to be sufficiently large, see [50] for details.
- 5.
To construct \(\varphi \) find a Möbius transformation \(\psi :\mathbb D\rightarrow \mathbb H\) which maps \(e^{i\theta }\) to \(\infty \) and y to i. Then \(\{z,w\}\) map to \(\{1-it,1+it\}\). Now reflect using \(z\mapsto -\overline{z}\), and go back using \(\psi ^{-1}\).
- 6.
Since \(\mathrm {Fix}(\varGamma )\) is countable, \(\varOmega \) is a \(G_\delta \)-subset of \(\partial \mathbb D\). By Alexandrov’s theorem, there is a metric on \(\varOmega \) which turns it into a complete separable metric space, and whose Borel sets are precisely the intersections of Borel subsets of \(\partial \mathbb D\) with \(\varOmega \).
References
J. Aaronson: An introduction to infinite ergodic theory. Mathematical Surveys and Monographs, 50. American Mathematical Society, Providence, RI, 1997. xii+284 pp. ISBN: 0-8218-0494-4
J. Aaronson, M. Denker, and A.M. Fisher: Second order ergodic theorems for ergodic transformations of infinite measure spaces. Proc. Amer. Math. Soc. 114 (1992) no. 1, 115–127.
J. Aaronson, H. Nakada, O. Sarig, and R. Solomyak: Invariant measures and asymptotics for some skew products. Israel J. Math. 128 (2002), 93–134.
J. Aaronson, O. Sarig, and R. Solomyak: Tail-invariant measures for some suspension semiflows. Discrete Contin. Dyn. Syst. 8 (2002), no. 3, 725–735.
J. Aaronson and B. Weiss: On the asymptotics of a 1-parameter family of infinite measure preserving transformations. Bol. Soc. Brasil. Mat. (N.S.) 29 (1998), no. 1, 181–193.
M. Babillot: On the classification of invariant measures for horospherical foliations on nilpotent covers of negatively curved manifolds. In: Random walks and geometry (V.A. Kaimanovich, Ed.) de Gruyter, Berlin (2004), 319–335.
M. Babillot and F. Ledrappier: Lalley’s theorem on periodic orbits of hyperbolic flows. Ergodic Theory Dynam. Systems 18 (1998), no. 1, 17–39.
M. Babillot and F. Ledrappier: Geodesic paths and horocycle flows on Abelian covers. Lie groups and ergodic theory (Mumbai, 1996), 1–32, Tata Inst. Fund. Res. Stud. Math. 14, Tata Inst. Fund. Res., Bombay, (1998).
M. Bachir Bekka: Ergodic theory and topological dynamics of group actions on homogeneous spaces, London Math. Soc. Lecture Notes Series 269, Cambridge University Press, 2013.
Philippe Bougerol and Laure Élie: Existence of positive harmonic functions on groups and on covering manifolds. Ann. Inst. H. Poincaré Probab. Statist. 31 (1995), no. 1, 59–80.
M. Burger: Horocycle flow on geometrically finite surfaces. Duke Math. J. 61 (1990), no. 3, 779–803.
Gustave Choquet and Jacques Deny: Sur l’équation de convolution \(\mu =\mu \ast \sigma \). (French) C. R. Acad. Sci. Paris 250 1960 799–801.
J.-P. Conze and Y. Guivarc’h: Propriété de droite fixe et fonctions harmoniques positives. (French) Théorie du potentiel et analyse harmonique (Exposés des Journées de la Soc. Math. France, Inst. Recherche Math. Avancée, Strasbourg, 1973), pp. 126–132. Lecture Notes in Math., Vol. 404, Springer, Berlin, 1974.
Y. Coudene: Cocycles and stable foliations of Axiom A flows, Ergodic Th. & Dynam. Syst. 21 (2001), 767–774.
F. Dal’bo: Remarques sur le spectre des longueurs d’une surface et comptages. Bol. Soc. Brasil. Mat. (N.S.) 30 (1999), no. 2, 1991.
S. G. Dani: Invariant measures of horospherical flows on noncompact homogeneous spaces. Invent. Math. 47 (1978), no. 2, 101–138.
S. G. Dani and J. Smillie: Uniform distribution of horocycle orbits for Fuchsian groups. Duke Math. J. 51 (1984), 185–194.
J. Feldman and C. C. Moore: Ergodic equivalence relations, cohomology, and von Neumann algebras. I. Trans. Amer. Math. Soc. 234 (1977), no. 2, 289–324.
A. Fisher: Convex-invariant means and a pathwise central limit theorem. Adv. in Math. 63 (1987), no. 3, 213–246.
A. M. Fisher: Integer Cantor sets and an order-two ergodic theorem. Ergodic Theory Dynam. Systems 13 (1993), no. 1, 45–64.
H. Furstenberg: The unique ergodicity of the horocycle flow. Springer Lecture Notes 318 (1972), 95–115.
H. Furstenberg: Recurrence in ergodic theory and combinatorial number theory. M. B. Porter Lectures. Princeton University Press, Princeton, N.J., 1981. xi+203 pp.
Y. Guivarc’h: Sur la représentation intégrale des fonctions harmoniques et des fonctions propres positives dans un espace riemannien symétrique. Bull. Sci. Math. (2) 108 (1984), no. 4, 373–392.
Y. Guivarc’h and A. Raugi: Products of random matrices: convergence theorems. In Random matrices and their applications (Brunswick, Maine, 1984), 31–54, Contemp. Math., 50, Amer. Math. Soc., Providence, RI, (1986).
E. Hopf: Ergodentheorie, Ergeb. Mat. vol. 5, Springer, Berlin, 1937.
E. Hopf: Ergodic theory and the geodesic flow on surfaces of constant negative curvature, Bull. AMS 77 (1971), 863–877.
J. H. Hubbard: Teichmüller Theory and applications to geometry, topology, and dynamics. Volume 1: Teichmüller theory. xx+459 pages. Matrix Edition (2006).
V. A. Kaimanovich: Ergodic properties of the horocycle flow and classification of Fuchsian groups. J. Dynam. Control Systems 6 (2000), no. 1, 21–56.
F. I. Karpelevich: The geometry of geodesics and the eigenfunctions of the Laplacian on symmetric spaces. Trans. Moskov. Math. Soc. 14 48–185 (1965).
S. Katok: Fuchsian groups. x+175 pages. The U. of Chicago Press (1992).
A. Katsuda and T. Sunada: Closed orbits in homology classes. Inst. Hautes Études Sci. Publ. Math. No. 71 (1990), 5–32.
S. Lalley: Closed geodesics in homology classes on surfaces of variable negative curvature, Duke Math. J., 55 (1989), 795–821.
F. Ledrappier: Invariant measures for the stable foliation on negatively curved periodic manifolds, Ann. Inst. Fourier 58 number 1 (2008), 85–105.
F. Ledrappier and O. Sarig: Unique ergodicity for non-uniquely ergodic horocycle flows. Discrete Contin. Dyn. Syst. 16 (2006), no. 2, 411–433.
F. Ledrappier and O. Sarig: Invariant measures for the horocycle flow on periodic hyperbolic surfaces. Israel J. Math. 160, 281–317 (2007).
F. Ledrappier and O. Sarig: Fluctuations of ergodic sums for horocycle flows on\({\mathbb{Z}}^d\)-covers of finite volume surfaces. Discrete Contin. Dyn. Syst. 22 (2008), no. 1-2, 247–325.
V. Lin and Y. Pinchover: Manifolds with group actions and elliptic operators. Mem. Amer. Math. Soc. 112 (1994), no. 540, vi+78 pp.
Terry Lyons and Dennis Sullivan: Function theory, random paths and covering spaces. J. Differential Geom. 19 (1984), no. 2, 299–323.
G. Margulis: Positive harmonic functions on nilpotent groups. Dokl. Akad. Nauk SSSR 166 1054–1057 (Russian); translated as Soviet Math. Dokl. 7 1966 241–244.
S. J. Patterson: The limit set of Fuchsian group, Acta Math. 136 (1976), 241–273.
M. Pollicott: \({\mathbb{Z}}^d\)-covers of horospheric foliations, Discrete Continuous Dynam. Syst. 6 (2000), 599–604.
M. Ratner: A central limit theorem for У-flows on three-dimensional manifolds. (Russian) Dokl. Akad. Nauk SSSR 186 (1969) 519–521.
M. Ratner: On Raghunathan’s measure conjecture. Ann. of Math. (2) 134 (1991), no. 3, 545–607.
M. Ratner: Raghunathan’s topological conjecture and distributions of unipotent flows. Duke Math. J. 63 (1991), no. 1, 235–280.
A. Raugi: Mesures invariantes ergodiques pour des produits gauches. Bull. Soc. Math. France 135 (2007), no. 2, 247–258.
M. Rees: Divergence type of some subgroups of finitely generated Fuchsian groups. Ergodic Theory Dynamical Systems 1 (1981), no. 2, 209–221.
T. Roblin: Sur l’ergodicité rationnelle et les propriétés ergodiques du flot géodésique dans les variétés hyperboliques. Ergodic Theory Dynam. Systems 20 (2000), no. 6, 1785–1819.
T. Roblin: Ergodicité et équidistribution en courbure négative. Mém. Soc. Math. Fr. (N.S.) 95 (2003), vi+96 pp.
O. Sarig: Invariant measures for the horocycle flow on Abelian covers. Inv. Math. 157, 519–551 (2004).
O. Sarig: The horocyclic flow and the Laplacian on hyperbolic surfaces of infinite genus. Geom. Funct. Anal. 19 (2010), no. 6, 1757–1812.
O. Sarig and B. Schapira: The generic points for the horocycle flow on a class of hyperbolic surfaces with infinite genus. Int. Math. Res. Not. IMRN 2008, Art. ID rnn 086, 37 pp.
B. Schapira: Equidistribution of the horocycles of a geometrically finite surface. Int. Math. Res. Not. 40, 2447–2471 (2005).
K. Schmidt: Cocycles on ergodic transformation groups. Macmillan Lectures in Mathematics, Vol. 1. Macmillan Company of India, Ltd., Delhi, 1977. 202 pp. (Available from the author’s homepage.)
C. Series: Geometrical methods of symbolic coding. In Ergodic Theory, Symbolic Dynamics, and Hyperbolic Spaces Edited by T. Bedford, M. Keane, C. Series. Oxford Univ. Press (1991).
R. Solomyak: A short proof of the ergodicity of the Babillot-Ledrappier measures, Proc. AMS 129 (2001), 3589–3591.
A. N. Starkov: Fuchsian groups from the dynamical viewpoint, J. Dynamics and Control Systems 1 (1995), 427–445.
J. Stillwell: Geometry of surfaces. Universitext. Springer-Verlag, New York, 1992. xii+216 pp. ISBN: 0-387-97743-0
D. Sullivan: The density at infinity of a discrete group of hyperbolic motions. Inst. Hautes Études Sci. Publ. Math. No. 50 (1979), 171–202.
D. Sullivan: Related aspects of positivity in Riemannian geometry. J. Diff. Geom. 25 327–351 (1987).
R. Zweimüller: Hopf’s ratio ergodic theorem by inducing. Colloq. Math. 101 (2004), no. 2, 289–292.
Acknowledgements
This set of notes constituted the basis for a series of lectures given in April 2015 as part of the program “Geometric and ergodic aspects of group actions,” at the Tata Institute for Fundamental Research, Mumbai. The author would like to thank the organizers of the program and the staff of TIFR for the kind hospitality. The author acknowledges the support of ISF grants 1149/18 and 199/14.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
6 Appendix 1: Busemann’s Function
Busemann’s function. Suppose \(z,w\in \mathbb D\) and \(e^{i\theta }\in \partial \mathbb D\). Busemann’s function \(b_{e^{i\theta }}(z,w)\) is the signed hyperbolic distance from \(\mathrm {Hor}_z(e^{i\theta })\) to \(\mathrm {Hor}_w(e^{i\theta })\): the solution s to the equation \(g^s[\mathrm {Hor}_z(e^{i\theta })]=\mathrm {Hor}_w(e^{i\theta })]\) (Fig. 10).
Theorem 25
(The basic identity for Busemann’s function) For every \(\varphi \in \)Möb\((\mathbb D)\), \(b_{\varphi (e^{i\theta })}(0,\varphi (0))=-\log |\varphi '(e^{i\theta })|\).
Proof
The following properties are obvious:
-
(I)
\(b_{\varphi (e^{i\alpha })}(\varphi (z_1),\varphi (z_2))=b_{e^{i\alpha }}(z_1,z_2)\) for all hyperbolic isometries \(\varphi \) (orientation reversing included).
-
(II)
\(b_{e^{i\alpha }}(z_1,z_2)+b_{e^{i\alpha }}(z_2,z_3)=b_{e^{i\alpha }}(z_1,z_3)\).
-
(III)
\((e^{i\theta },z,w)\mapsto b_{e^{i\theta }}(z,w)\) is Borel measurable.
We claim that (I), (II), and (III) determine \((e^{i\theta },z,w)\mapsto b_{e^{i\theta }}(z,w)\) up to a multiplicative constant. Suppose \(c_{e^{i\theta }}(z,w)\) satisfies (I), (II) and (III).
First, \(c_{e^{i\theta }}(z,z)=0\) for all z, because of (II).
Second, \(c_{e^{i\theta }}(z,w)=0\) whenever \(w\in \mathrm {Hor}_{e^{i\theta }}(z)\). To see this, let y denote the midpoint of the horocyclic arc connecting z to w, and let \(\gamma \) denote the geodesic from y to \(e^{i\theta }\). Let \(\varphi \) denote the hyperbolic reflection w.r.t. \(\gamma \),Footnote 5 then \(\varphi (e^{i\theta })=e^{i\theta }\) and \(\varphi (z)=w\), \(\varphi (w)=z\). By (I) and (II), \(0=c_{e^{i\theta }}(z,w)+c_{e^{i\theta }}(w,z)=c_{e^{i\theta }}(z,w)+c_{\varphi (e^{i\theta })}(\varphi (w),\varphi (z))=2c_{e^{i\theta }}(z,w)\), proving that \(c_{e^{i\theta }}(z,w)=0\).
Third, \(c_{e^{i\theta }}(z,w)\) is determined by the values of the function \(c_1(0,t)\) for t real. To see this use a Möbius transformation to map \(e^{i\theta },z\) to 1, 0. Let \(w^*\) denote the image of w, and let t denote the intersection of \(\mathrm {Hor}_1(w)\) with the real line. Then \(c_{e^{i\theta }}(z,w)=c_1(0,w^*)=c_1(0,t)+c_1(t,w^*)=c_1(0,t)\).
Finally, \(c_1(0,t)=\mathrm {const.\,}\mathrm {dist}\,(0,t)\) \((t\in \mathbb R)\) because (I) implies that \(c_1(t_1,t_2)\) is a function of the hyperbolic distance between \(t_1,t_2\), (II) says that this dependence is additive, and (III) says it is Borel.
Here is a construction of a function \(c_{e^{i\alpha }}(z,w)\) which satisfies (I), (II) and (III): Let \(\lambda _z\) denote the harmonic measure on \(\partial \mathbb D\) at z, defined by \(d\lambda _z(e^{i\theta })=P(e^{i\theta },z)d\theta \), where \(P(e^{i\theta },z)=\frac{1-|z|^2}{|e^{i\theta }-z|^2}\) (Poisson’s kernel). We claim that
satisfies (I),(II), and (III).
(III) is obvious. (II) is the chain rule for Radon–Nikodym derivatives. To see (I) we recall that Poisson’s formula says that for every \(f\in C(\partial \mathbb D)\), \(F(z):=\int _{\partial \mathbb D}f d\lambda _z\) is the unique harmonic function on \(\mathbb D\) with boundary values \(f(e^{i\theta })\). For every \(f\in C(\partial \mathbb D)\) and \(\varphi \in \text {M}\ddot{\mathrm{o}}\text {b}(\mathbb D)\) \( \int f d\lambda _z\circ \varphi ^{-1}=\int f\circ \varphi d\lambda _z=F(\varphi (z))=\int _{\partial \mathbb D}f d\lambda _{\varphi (z)}, \) so \(\lambda _z\circ \varphi ^{-1}=\lambda _{\varphi (z)}\). This implies (I):
By the first part of the proof, \(b_{e^{i\theta }}(z,w)=\mathrm {const.\,}\log \frac{P(e^{i\theta },z)}{P(e^{i\theta },w)}\). Since
-
\(c_1(0,r)=\log \left( \frac{P(1,0)}{P(1,r)}\right) =-\log P(1,r)=-\log \frac{1-r^2}{(1-r)^2}=\log \frac{1-r}{1+r}\),
-
\(b_1(0,r)=\int _0^r \frac{2dt}{1-t^2}dt=\int _0^r\left( \frac{1}{1-t}+\frac{1}{1+t}\right) dt=\log \frac{1+r}{1-r}\),
the constant equals \((-1)\). We obtain the identity \(b_{e^{i\theta }}(z,w)=-\log \left( \frac{d\lambda _z}{d\lambda _w}(e^{i\theta })\right) \).
It follows that \(b_{\varphi (e^{i\theta })}(0,\varphi (0))=-\log \frac{d\lambda _0}{d\lambda _{\varphi (0)}}(e^{i\theta })=\log \frac{d\lambda _0\circ \varphi ^{-1}}{d\lambda _0}[\varphi (e^{i\theta })]\). Since \(\lambda _0\) is Lebesgue’s measure, this equals \(\log |(\varphi ^{-1})'(\varphi (e^{i\theta }))|=-\log |\varphi '(e^{i\theta })|\). \(\square \)
Proof of Theorem 1 part (3): Fix \(\varphi \in \text {M}\ddot{\mathrm{o}}\text {b}(\mathbb D)\), we have to show that
Draw in \(\mathbb D\) \(\omega =(h^{t_0}\circ g^{s_0})[\omega (e^{i\theta _0})]\) together with \(\mathrm {Hor}(\omega )\) and \(\mathrm {Hor}(\omega (e^{i\theta _0}))\). Add to the picture the geodesic rays of \(\omega (e^{i\theta _0})\) and \(\omega \). Now draw the image of these figures by \(\varphi \) (Fig. 11).
The kan-coordinates of \(\varphi (\omega )\) are \( (\varphi (e^{i\theta _0}),s_0+b_{\varphi (e^{i\theta _0})}(0,\varphi (0)),t_0+\delta _0), \) where \(\delta _0\) is some function of \(0,\varphi (0),s_0, e^{i\theta _0}\). (\(*\)) follows from the basic identity for the Busemann function. \(\square \)
Proof of Theorem24. The theorem asserts that if \(\varphi \in \varGamma \), \(e^{i\theta }\in \partial \mathbb D\), and \(|\varphi (e^{i\theta })-e^{i\theta }|<1\), then \( |R(\varphi ,e^{i\theta })-B(\gamma ,\widetilde{\gamma })|\le 4|e^{i\theta }-e^{i\theta }|^2, \) where
- \(\circ \):
-
\(R(\varphi ,e^{i\theta })=-\log |\varphi '(e^{i\theta })|\) (the Radon–Nikodym cocycle).
- \(\circ \):
-
\(\gamma :=\) the projection to \(\varGamma \setminus \mathbb D\) of \(\gamma [-e^{i\theta },e^{i\theta }]\), the \(\mathbb D\)-geodesic from \(-e^{i\theta }\) to \(e^{i\theta }\).
- \(\circ \):
-
\(\widetilde{\gamma }:=\) the projection to \(\varGamma \setminus \mathbb D\) of \(\gamma [-e^{i\theta },\varphi (e^{i\theta })]\), the geodesic from \(-e^{i\theta }\) to \(\varphi (e^{i\theta })\).
- \(\circ \):
-
\(B(\gamma ,\widetilde{\gamma })=\mathrm {dist}\,_{\widetilde{\gamma }}(\omega _2,\omega _2^*)-\mathrm {dist}\,_\gamma (\omega _1,\omega _1^*)\) for some (any) \(\omega _1,\omega _1^*\in \gamma \), \(\omega _2,\omega _2^*\in \widetilde{\gamma }\), s.t. \( \mathrm {dist}\,(g^{-s}\omega _1,g^{-s}\omega _2)\xrightarrow [s\rightarrow \infty ]{}0\text { and } \mathrm {dist}\,(g^{s}\omega _1^*,g^s\omega _2^*)\xrightarrow [s\rightarrow \infty ]{}0. \)
We take \(\omega _1=\omega _1^*=\) vector based at 0 and pointing at \(e^{i\theta }\), \(\omega _2:=\) intersection of \(\gamma [-e^{i\theta },\varphi (e^{i\theta })]\) and \(\mathrm {Hor}_{-e^{i\theta }}(0)\) and \(\omega _2^*:=\) intersection of \(\gamma [-e^{i\theta },\varphi (e^{i\theta })]\) and \(\varphi [\mathrm {Hor}_{e^{i\theta }}(0)]=\mathrm {Hor}_{\varphi (e^{i\theta })}(\varphi (0))\) (Fig. 12). Add to the picture \(\omega _3:=\) intersection of \(\gamma [-e^{i\theta },\varphi (e^{i\theta })]\) and \(\mathrm {Hor}_{\varphi (e^{i\theta })}(0)\).
Clearly \( B(\gamma ,\widetilde{\gamma })=\mathrm {dist}\,_{\gamma [-e^{i\theta },\varphi (e^{i\theta })]}(\omega _2,\omega _2^*)=\mathrm {dist}\,(\omega _3,\omega _2^*) -\mathrm {dist}\,(\omega _3,\omega _2) \). The first summand is the signed distance from \(\mathrm {Hor}_{\varphi (e^{i\theta })}(0)\) and \(\mathrm {Hor}_{\varphi (e^{i\theta })}(\varphi (0))\). This is \(b_{\varphi (e^{i\theta })}(0,\varphi (0))=-\log |\varphi '(e^{i\theta })|=R(\varphi ,e^{i\theta })\). So
To estimate \(\delta \), let \(\vartheta :\mathbb D\rightarrow \mathbb H\) be the Möbius map which sends \(e^{i\theta }\mapsto 0\), \(-e^{i\theta }\mapsto \infty \), and \(0\mapsto i\). This map maps \(\mathrm {Hor}_{-e^{i\theta }}(0)\) to the horizonal line \(y=1\), and \(\mathrm {Hor}_{\varphi (e^{i\theta })}(0)\) to a circle passing through i which is tangent to the real axis at \(\vartheta (\varphi (e^{i\theta }))\). So \(\delta \) is the hyperbolic distance between the peak of this circle and \(y=1\) (Fig. 13). It is clear from Fig. 13 that \(\delta =O(|\vartheta (e^{i\theta })-\vartheta [\varphi (e^{i\theta })]|^2)\). A precise calculation using an explicit formula for \(\vartheta \) shows that \(|\delta |\le 4|e^{i\theta }-\varphi (e^{i\theta })|^2\). \(\square \)
Notes and references. The proof of Theorem 25 is taken from [28]. The proof of Theorem 24 is taken from [50].
7 Appendix 2: The Cocycle Reduction Theorem
1.1 7.1 Preliminaries on Countable Equivalence Relations
Suppose  is a standard Borel space (a complete and separable metric space equipped with the \(\sigma \)-algebra of Borel sets). Every measurable group action on \(\varOmega \) generates an equivalence relation
is a standard Borel space (a complete and separable metric space equipped with the \(\sigma \)-algebra of Borel sets). Every measurable group action on \(\varOmega \) generates an equivalence relation
This is called the orbit relation of the action.
The orbit relation keeps information on the orbits as sets, but forgets the way these sets are parametrized by the group. The language of equivalence relations, which we review below, is designed to handle dynamical properties such as invariance or ergodicity, which only depend on the structure of orbits as unparameterized sets. We will comment at the end of the section on why this is useful.
Countable Borel equivalence relations: These are subsets \(\mathfrak G\subset \varOmega \times \varOmega \) such that
-
1.
\(x\sim y\Leftrightarrow (x,y)\in \mathfrak G\) is a reflexive, symmetric, and transitive relation;
-
2.
the equivalence classes of \(\sim \) are all finite or countable;
-
3.
\(\mathfrak G\) is in the product \(\sigma \)-algebra
 .
.
For example, suppose G is a countable group of bi-measurable maps \(g:\varOmega \rightarrow \varOmega \). The orbit relation of G is the countable Borel equivalence relation
Theorem 26
(Feldman and Moore) Every countable Borel equivalence relation on a standard measurable space  is the orbit relation of some countable group action on X.
is the orbit relation of some countable group action on X.
Corollary 2
Suppose \(\mathfrak G\) is a countable Borel equivalence relation on a standard measurable space  .
.
-
1.
If
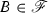 , then \(\mathrm {Sat}(B):=\{x\in \varOmega :\exists y\in B\text { s.t. }(x,y)\in \mathfrak G\}\) is measurable.
, then \(\mathrm {Sat}(B):=\{x\in \varOmega :\exists y\in B\text { s.t. }(x,y)\in \mathfrak G\}\) is measurable. -
2.
If
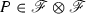 , then \(\{x\in \varOmega : (x,y)\in \mathfrak G\Rightarrow (x,y)\in P\}\) is measurable.
, then \(\{x\in \varOmega : (x,y)\in \mathfrak G\Rightarrow (x,y)\in P\}\) is measurable.
Proof
Use the Feldman–Moore Theorem to realize \(\mathfrak G\) as an orbit relation of a countable group G. Then  , and
, and
This set is measurable because G is countable, and \(x\mapsto (x,g(x))\) is measurable. \(\square \)
“Almost everywhere in \(\mathfrak G\)”: Let P(x, y) be a measurable property of pairs \((x,y)\in X\times X\), i.e.,  .
.
Suppose \(\mu \) is a measure on X. We say that P holds \(\mu \)-a.e. in \(\mathfrak G\), if \(\{x\in X: (x,y)\in \mathfrak G\Rightarrow (x,y)\in P\}\) has full measure. The previous corollary guarantees measurability.
Holonomies, invariant functions, invariant measures: Suppose \(\mathfrak G\) is a countable Borel equivalence relation.
-
A \(\mathfrak G\)-holonomy is a bi-measurable bijection \(\kappa :A\rightarrow B\) where \(\mathrm {dom}(\kappa ):=A\), \(\mathrm {im}(\kappa ):=B\) are measurable sets and \((x,\kappa (x))\in \mathfrak G\) for all \(x\in \mathrm {dom}(\kappa )\).
-
A function \(f:\varOmega \rightarrow \mathbb R\) is called \(\mathfrak G\) -invariant, if \(f\circ \kappa |_{\mathrm {dom}(\kappa )}=f|_{\mathrm {dom}(\kappa )}\) for all \(\mathfrak G\)-holonomies \(\kappa \). Equivalently, \(f(x)=f(y)\) whenever \((x,y)\in \mathfrak G\).
-
A (possibly infinite) measure \(\mu \) on \(\varOmega \) is called \(\mathfrak G\) -invariant if \(\mu \circ \kappa |_{\mathrm {dom}(\kappa )}=\mu |_{\mathrm {dom}(\kappa )}\) for all \(\mathfrak G\)-holonomies \(\kappa \).
-
A \(\mathfrak G\)-invariant measure is called ergodic, if every measurable \(\mathfrak G\)-invariant function is equal a.e. to a constant function.
Lemma 8
Suppose G is a countable group acting measurably on  , and let \(\mu \) be a (possibly infinite) measure on \((\varOmega ,\mathscr {F})\). Let \(\mathfrak G:=\mathfrak {orb}(G)\), then
, and let \(\mu \) be a (possibly infinite) measure on \((\varOmega ,\mathscr {F})\). Let \(\mathfrak G:=\mathfrak {orb}(G)\), then
-
1.
\(\mu \) is G-invariant iff \(\mu \) is \(\mathfrak G\)-invariant.
-
2.
\(\mu \) is G-ergodic iff \(\mu \) is \(\mathfrak G\)-ergodic.
The proof is easy and we leave it to the reader.
Induced equivalence relations: Suppose B is a measurable set with positive measure. The induced relation on B is
Lemma 9
Suppose \(\mu \) is a measure on \(\varOmega \) and \(\mu (B)>0\). If \(\mu \) is \(\mathfrak G\)-invariant, then \(\mu |_B\) is \(\mathfrak G[B]\)-invariant. If \(\mu \) is \(\mathfrak G\)-ergodic, then \(\mu |_B\) is \(\mathfrak G[B]\)-ergodic.
Proof
The first statement is trivial, so we prove only the second. Suppose \(f:B\rightarrow \mathbb R\) is \(\mathfrak G[B]\)-invariant. The saturation of B is a \(\mathfrak G\)-invariant measurable set of positive measure (because it contains B). By ergodicity, \(\mathrm {Sat}(B)\) has full measure. Define
The definition is proper because f is \(\mathfrak G[B]\)-invariant. Clearly, F is \(\mathfrak G\)-invariant. By \(\mathfrak G\)-ergodicity, F is equal a.e. on \(\varOmega \) to a constant function. So \(f=F|_B\) is equal a.e. on B to a constant function. \(\square \)
Cocycles and skew-product extensions: Suppose \(\mathfrak G\) is a countable Borel equivalence relation on a standard Borel space  .
.
-
A \(\mathfrak G\)-cocycle is a measurable map \(\varPhi :\mathfrak G\rightarrow \mathbb R\) s.t. \( \varPhi (x,y)+\varPhi (y,z)=\varPhi (x,z)\) for all \((x,y),(y,z)\in \mathfrak G\). Necessarily \(\varPhi (x,x)=0\) and \(\varPhi (x,y)=-\varPhi (y,x)\).
-
The \(\varPhi \)-extension of \(\mathfrak G\) is the equivalence relation on \(\varOmega \times \mathbb R\)
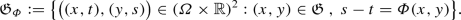
-
Every \(\mathfrak G\)-holonomy \(\kappa :A\rightarrow B\) generates a \(\mathfrak G_\varPhi \)-holonomy \(\kappa _\varPhi :A\times \mathbb R\rightarrow B\times \mathbb R\) given by \( \kappa _\varPhi (x,t)=(\kappa (x),t+\varPhi (x,\kappa (x))). \)
Example: Radon–Nikodym extensions. Suppose \(\varGamma \subset \text {M}\ddot{\mathrm{o}}\text {b}(\mathbb D)\) is countable and discrete group. Let \(\mathrm {Fix}(\varGamma ):=\{z\in \partial \mathbb D: \exists g\in \varGamma \setminus \{id\}\text { s.t. }g(z)=z\}\), and set
together with its Borel subsets. This is a standard Borel space.Footnote 6
Let \(\mathfrak G:=\mathfrak {orb}(\varGamma )\). If \((x,y)\in \mathfrak G\) then there exists a unique \(g\in \varGamma \) such that \(y=g(x)\) (otherwise x is a fixed point of a nontrivial element of \(\varGamma \)). Let
This is a \(\mathfrak G\)-cocycle, because of the chain rule. Then

Lemma 10
Suppose \(\mu \) is \(\mathfrak G_\varPhi \)-ergodic invariant measure on \(X\times \mathbb R\), then for every  and \(K_1,K_2\subseteq \mathbb R\) compact such that \(\mu (A\times K_1), \mu (B\times K_2)>0\) one can find a \(\mathfrak G\)-holonomy \(\kappa \) such that \(\mu [\kappa _\varPhi (A\times K_1)\cap (B\times K_2)]>0\).
and \(K_1,K_2\subseteq \mathbb R\) compact such that \(\mu (A\times K_1), \mu (B\times K_2)>0\) one can find a \(\mathfrak G\)-holonomy \(\kappa \) such that \(\mu [\kappa _\varPhi (A\times K_1)\cap (B\times K_2)]>0\).
Proof
By the Feldman–Moore Theorem, \(\mathfrak G\) is the orbit relation of a countable group G. Every \(g\in G\) determines a \(\mathfrak G_\varPhi \) holonomy with domain \(X\times \mathbb R\) via \(g_\varPhi (x,s)=(g(x),s+\varPhi (x,g(x)))\). The set \(\bigcup _{g\in G}g_\varPhi (A)\) is a measurable \(\mathfrak G_\varPhi \)-invariant set, whence a set of full measure. So for some \(g\in G\), \(\mu [g_\varPhi (A\times K_1)\cap (B\cap K_2)]>0\). \(\square \)
Why do we need all this general nonsense? The Feldman–Moore Theorem says that any countable equivalence relation is the orbit relation of some measurable action of a countable group. The independent-minded reader may wonder what is the point of working in this more abstract setup of equivalence relations, when it is not really more general. There are two main reasons:
-
1.
The language of equivalence relations is convenient in scenarios when it is easier to decide when two points belong to the same orbit than it is to find the parametrization of the orbit and calculate the actual group element which maps one to the other. This is the case for horocycle flows: There is a simple geometric criterion for deciding when two unit tangent vectors belong to the same horocycle—their geodesic rays are forward asymptotic. But to calculate the horocyclic time it takes to move from one to the other is much more subtle.
-
2.
Induction: It is difficult to construct the induced action of a group on a subset, especially in cases when the individual elements of the group are not conservative (as is the case for hyperbolic or parabolic Möbius transformations). But as we saw above, it is very easy to induce equivalence relations on subsets. Of course, by Feldman–Moore, the induced orbit equivalence relation is the orbit relation of some other countable group action—but constructing that group explicitly is not easy.
We will use the operation of inducing repeatedly in the proof of the cocycle reduction theorem. This is the reason we need to use countable equivalence relations.
1.2 7.2 The Cocycle Reduction Theorem
Let \(\mathfrak G\) be a countable Borel equivalence relation on a standard Borel space \((X,\mathscr {B})\). Let \(\varPhi :\mathfrak G\rightarrow \mathbb R\) be a measurable cocycle, and suppose \(\mu \) is a (possibly infinite) \(\mathfrak G_\varPhi \)-ergodic invariant measure on \(X\times \mathbb R\). We assume that \(\mu \) is locally finite: \(\mu (X\times K)<\infty \) for all compact sets \(K\subset \mathbb R\).
A coboundary is a cocycle of the form \(\partial u(x,y):=u(y)-u(x)\). Two cocycles which differ by a coboundary are called cohomologous.
The a.e. range of a cocycle is the smallest closed subgroup of \(\mathbb R\) such that \(\varPhi (x,y)\in H\) \(\mu \)-a.e. in \(\mathfrak G_\varPhi \).
Sometimes one can reduce the range of a cocycle \(\varPhi \) by subtracting from it a coboundary. For example, if \(\varPhi \) is a \(\mathbb Z\)-valued \(\mathfrak G\)-cocycle, but u(x) is real-valued, then \(\varPhi +\partial u\) will be an \(\mathbb R\)-valued cocycle. If we subtract \(\partial u\), then we’re back to a \(\mathbb Z\)-valued cocycle.
How much can we reduce the range by subtracting a coboundary? The cocycle reduction theorem says that the best we can do is
Here \(g^s:X\times \mathbb R\rightarrow X\times \mathbb R\) is the flow \(g^s(x,t)=(x,t+s)\), \(\mu \circ g^s\sim \mu \) means that \(\mu (g^s E)=0\Leftrightarrow \mu (E)=0\) for all measurable \(E\subset X\times \mathbb R\), and \(\mu \circ g^s\perp \mu \) means that \(\mu \circ g^s\) and \(\mu \) are carried by disjoint sets. Equality \(\overset{!}{=}\) is a consequence of ergodicity: Two ergodic invariant measures of the same countable equivalence relation (equiv. countable group action) are either proportional or they are mutually singular.
Theorem 27
(Cocycle reduction theorem) If \(\mu \) is a locally finite \(\mathfrak G_\varPhi \)-ergodic and invariant measure on \(X\times \mathbb R\), then there exists a Borel function \(u:X\rightarrow \mathbb R\) s.t.
-
1.
The set \(\{(x,t):t\in u(x)+H_\mu \}\) has full \(\mu \)-measure.
-
2.
\(\varPhi (x,y)+u(x)-u(y)\in H_\mu \) \(\mu \)–a.e. in \(\mathfrak G_\varPhi \).
-
3.
\(H_\mu \) is contained in any closed subgroup of \(\mathbb R\) with property 1 or with property 2.
So \(H_\mu \) is the minimal \(\mu \)–a.e. range of the cocycles which are \(\mu \)-a.e. cohomologous to \(\varPhi \).
Caution! The reader should note the subtlety in the quantifier in part 2. The measure \(\mu \) is a measure on \(X\times \mathbb R\), not X, and it is not assumed a priori to be a product measure. Therefore, although the \(\mathbb R\)-coordinates of (x, t), (y, s) are not mentioned explicitly, they do matter—because of their influence on the support of \(\mu \). Think of the case when \(\mu \) is carried by the graph of a function.
The third part of the cocycle reduction theorem is easy:
Lemma 11
Suppose \(\mu \) is a locally finite \(\mathfrak G_\varPhi \)-ergodic invariant measure.
-
1.
\(H_\mu \) is a closed subgroup of \(\mathbb R\), so \(H_\mu =\{0\},c\mathbb Z\) or \(\mathbb R\).
-
2.
If \(u:X\rightarrow \mathbb R\) is measurable and H is a closed subgroup of \(\mathbb R\) s.t. \(\{(x,t):t\in u(x)+H\}\) has full measure, then \(H\supseteq H_\mu \).
-
3.
If \(u:X\rightarrow \mathbb R\) is measurable and H is a closed subgroup of \(\mathbb R\) s.t. \(\varPhi +\partial u\in H\) \(\mu \)–a.e. in \(\mathfrak G_\varPhi \), then \(H\supseteq H_\mu \).
Proof
To see the first part, note that there is no loss of generality in assuming that X is a compact metric space, because by Kuratowski’s theorem all standard Borel spaces are measurably isomorphic to such spaces. Now proceed as in the proof of Proposition 1 in Sect. 5.2.
The second part is done by checking that the support of \(\mu \) is invariant under \(g^s\) for all \(s\in H_\mu \).
The third part is done by observing that if \(\varPhi +\partial u\in H\) a.e. in \(\mathfrak G_\varPhi \), then the function \(F:X\times \mathbb R\rightarrow \mathbb R/H\), \(F(x,t):=t-u(x)+H\) is \(\mathfrak G_\varPhi \) invariant, therefore \(\mu \)-a.e. constant. So there exists \(c\in \mathbb R\) s.t. \(\{(x,t):t-u(x)\in c+H\}\) has full measure. Arguing as in part 2, we find that \(H\supseteq H_\mu \). \(\square \)
So \(H_\mu \) is contained in the a.e-range of every cocycle which cohomologous to \(\varPhi \). It remains to construct the coboundary which reduces the range to \(H_\mu \).
We sketch the proof of the cocycle reduction theorem below. For complete details, see [49].
1.3 7.3 The Proof in Case There Are No Square Holes
A square hole is a set \(B\times [a,b]\) where \(B\in \mathscr {B}\), \(\mu (B\times [a,b])=0\), and \(\mu (B\times \mathbb R)\ne ~0\).
Lemma 12
Under the assumptions of the cocycle reduction theorem, if \(\mu \) has no square holes, then \(\mu \circ g^s\sim \mu \) for all \(s\in \mathbb R\). (Here \(g^s(x,\xi )=(x,\xi +s)\).)
Proof
All standard Borel spaces are isomorphic to compact metric spaces, so there is no loss of generality in assuming that X is a compact metric space equipped with a metric d.
Assume by way of contradiction that \(\exists a\in \mathbb R\) s.t. \(\mu \circ g^a\not \sim \mu \). Since \(g^s\) commutes with \(\kappa _\varPhi \) for every \(\mathfrak G\)-holonomy \(\kappa \), \(\mu \circ g^a\) is \(\mathfrak G_\varPhi \)-ergodic and invariant. Two ergodic measures are either equivalent or they are mutually singular (exercise), so \(\mu \circ g^a\perp \mu \). Similarly, \(\mu \circ g^{-a}\perp \mu \), and \( \mu \perp \overline{\mu }:=\mu \circ g^a+\mu \circ g^{-a}. \)
Choose \(f:X\times \mathbb R\rightarrow [0,\infty )\) continuous with compact support s.t.
Since f has compact support, f is uniformly continuous. Choose \(\delta >0\) so that
We will use the assumption that there are no square holes to find a \(\mathfrak G\)-holonomy \(\kappa :A\rightarrow B\) with the following properties:
-
(a)
for all \(x\in A\), \(d(x,\kappa (x))<\delta \);
-
(b)
for all \(x\in A\), \(\min \{|\varPhi (x,\kappa (x))-a|,|\varPhi (x,\kappa (x))+a|\}<\delta \);
-
(c)
\(A\times \mathbb R\) has full measure.
Construction of \(\kappa \): Divide X into a finite pairwise disjoint collection of sets of diameter less than \(\delta \). We will construct \(\kappa \) on each cell U separately in such a way that \(\kappa (U)\subset U\). Then we will glue the pieces into one holonomy noting that bijectivity is not destroyed because the partition elements are disjoint.
To get (c), we only need to worry about partition sets U such that \(\mu (U\times \mathbb R)\ne 0\).
Fix some partition set U such that \(\mu (U\times \mathbb R)\ne 0\). Let \(B(t,r):=(t-r,t+r)\). Since there are no square holes,
Since \(\mu \) is \(\mathfrak G_\varPhi \)-ergodic, we can use Lemma 10 to construct a \(\mathfrak G\)-holonomy \(\kappa \) such that \(\mu [\kappa _\varPhi (U\times B(0,\delta /2))\cap (U\times B(a,\delta /2))]>0\).
Let \(A_1:=\mathrm {dom}(\kappa )\cap \kappa ^{-1}(U)\) and \(B_1:=\kappa (A_1)\), then \(\mu (A_1\times \mathbb R)>0\), \(\mu (B_1\times \mathbb R)>0\) and for all \(x\in A_1\),
So for all \(x\in A_1\), \(d(x,\kappa (x))<\delta \) and \(|\varPhi (x,\kappa (x))-a|<\delta \).
If \(A_1\times \mathbb R\) has full measure in \(U\times \mathbb R\) we are done and can continue to another partition element. If \(B_1\times \mathbb R\) has full measure in \(U\times \mathbb R\) then we are also done, because we can use \(\kappa ^{-1}\).
If \(A_1\times \mathbb R\) and \(B_1\times \mathbb R\) are of positive but non-full measure in \(U\times \mathbb R\), then we let \(\kappa _1:=\kappa \) and construct an extension of \(\kappa _1\) to a bigger domain inside U as follows. Since there are no square holes, \(\mu [(U\setminus A_1)\times B(0,\frac{\delta }{2})],\mu [(U\setminus B_1)\times B(a,\frac{\delta }{2})]\ne 0\). By Lemma 10, there is a \(\mathfrak G\)-holonomy \(\kappa '\) and sets \(A_1'\subset U\setminus A_1\), \(B_1'\subset U\setminus B_1\) such that \(\mu (A_1'\times \mathbb R),\mu (B_1'\times \mathbb R)\ne 0\) and
As before \(d(x,\kappa '(x))<\delta \) and \(|\varPhi (x,\kappa '(x))-a|<\delta \) for \(x\in A'\). Since \(\kappa ,\kappa '\) have disjoint domains and disjoint supports, \(\kappa _2:=\kappa _1\cup \kappa '\) is a well-defined holonomy from a subset of U to U.
It is now a standard matter to proceed by the “method of exhaustion” to show that there exists a holonomy \(\kappa _\infty \) with properties (a),(b) and such that one of \(\mathrm {dom}(\kappa _\infty )\times \mathbb R\), \(\mathrm {im}(\kappa _\infty )\times \mathbb R\) has full measure in \(U\times \mathbb R\). See [49] for details. In first case set \(\kappa |_U:=\kappa _\infty \). In the second case set \(\kappa |_U:=\kappa _\infty ^{-1}\). Now that we are done defining \(\kappa \) a.e. on U, we move to the next partition element. After finitely many steps, we are done.
Using the holonomy \(\kappa \) to prove the lemma: Let \(\kappa _\varPhi (x,t):=(\kappa (x),t+\varPhi (x,\kappa (x)))\).
-
\(\kappa _\varPhi \) preserves \(\mu \), because \(\kappa _\varPhi \) is a \(\mathfrak G_\varPhi \)-holonomy;
-
\(\min \{|f\circ \kappa _\varPhi ^{-1}-f\circ g^a|,|f\circ \kappa _\varPhi ^{-1}-f\circ g^{-a}|\}<\frac{1}{4\mu [f\ne 0]}\), because of (10).
So \(1=\int f d\mu =\int f d\mu \circ \kappa _\varPhi =\int _{\kappa _\varPhi [f\ne 0]}f\circ \kappa _\varPhi ^{-1}\, d\mu \le \int _{\kappa _\varPhi [f\ne 0]}(f\circ g^a+f\circ g^{-a})d\mu +\int _{\kappa _\varPhi [f\ne 0]}\frac{2}{4\mu [f\ne 0]}d\mu \le \int f d\overline{\mu }+\frac{1}{2}<\frac{3}{4}\). This contradiction shows that there can be no a s.t. \(\mu \circ g^a\not \sim \mu \). \(\square \)
Proof of the cocycle reduction theorem when there are no holes: The lemma shows that if there are no square holes, then \(H_\mu =\mathbb R\). In this case, the cocycle reduction theorem holds with \(u\equiv 0\).
1.4 7.4 The Proof in Case There Is a Square Hole
The proof proceeds by determining the support of \(\mu \) locally, and then globally:
-
1.
Step 1: There is a window \(W:=A\times [\alpha ,\beta ]\) with positive \(\mu \)-measure such that \( A\times [\alpha ,\beta ]=\{(x,u_0(x)):x\in A\}\mod \mu \) with \(u_0:A\rightarrow [\alpha ,\beta ]\) measurable.
-
2.
Step 2: \(A\times \mathbb R=\{(x,t): t\in u_0(x)+H_\mu \}\mod \mu \).
-
3.
Step 3: \(X\times \mathbb R=\{(x,t): t\in u(x)+H_\mu \}\mod \mu \) for \(u:X\rightarrow \mathbb R\) measurable such that \(u|_A=u_0\).
The main step is step 1; the other two steps follow from ergodicity and invariance. We will make repeated use of the following fact from measure theory:
Lemma 13
There exists a probability measure \(\nu \) on X and Radon measures \(\mu _x\) on \(\mathbb R\) such that for every nonnegative measurable and \(\mu \)-integrable function \(f:X\times \mathbb R\rightarrow [0,\infty )\),
For \(\nu \)–a.e. \(x\in X\), for every \(\mathfrak G\)-holonomy \(\kappa \) with \(x\in \mathrm {dom}(\kappa )\), \(\mu _{\kappa (x)}\circ \kappa _\varPhi =\mu _x\).
Sketch of proof (see [1, Chap. 1], [22, Chap. 2], [53, Corollary 6.9]). Fix \(\varphi :\mathbb R\rightarrow (0,1)\) such that \(\int \varphi (t)d\mu (x,t)=1\) (such a function exists by local finiteness). Then \(\varphi d\mu \) is a probability measure. Since \(X\times \mathbb R\) is a standard probability space, we have a fiber decomposition of \(\varphi \mu \) by general results in measure theory. Multiplying by \(1/\varphi \) we obtain a fiber decomposition for \(\mu \). Notice that \(\nu (E)\equiv \int _{E\times \mathbb R} \varphi (t)d\mu (x,t)\).
Any two fiber decompositions of \(\varphi \mu \) agree on a set of full measure, because \(\int f\varphi d\mu _x\) is a version of the conditional expectation of f on \(\mathscr {B}\otimes \{\varnothing ,\mathbb R\}\), and \(L^1(X\times \mathbb R)\) is separable.
Let G be a countable group of invertible transformations of X such that \(\mathfrak {orb}(G)=\mathfrak G\) (see the Feldman–Moore Theorem). Comparing the fiber decomposition of \(\mu \) to that of \(\mu \circ \kappa _\varPhi \) for \(\kappa \in G\), we find that for a.e. x, \(\mu _{\kappa (x)}\circ \kappa _\varPhi =\mu _x\) for all \(\kappa \in G\). Since G generates \(\mathfrak G\), this is the case for every \(\mathfrak G\)-holonomy s.t. \(\mathrm {dom}(\kappa )\ni x\). \(\Box \)
Step 1: If \(\mu \) has a square hole, then there is a set with positive measure \(W:=A\times [\alpha ,\beta ]\) and a measurable function \(u_0:A\rightarrow [\alpha ,\beta ]\) such that
-
(a)
for all \(((x,\xi ),(y,\eta ))\in \mathfrak G_\varPhi [W]\equiv \mathfrak G_\varPhi \cap W^2\), \(\varPhi (x,y)=u_0(y)-u_0(x)\);
-
(b)
\(W=\{(x,u_0(x)):x\in A\}\mod \mu \).
Proof
Let \(B\times [a,b]\) be a square hole: \(\mu (B\times [a,b])=0\), \(\mu (B\times \mathbb R)\ne 0\). Fix some \(s\in \mathbb R\setminus [a,b]\) and \(0<\varepsilon <\min \{\frac{1}{6}|a-b|,\frac{1}{2}|s-a|\}\) such that
Without loss of generality \(s<a\), otherwise change coordinates \((x,\xi )\leftrightarrow (x,-\xi )\).
Using Lemma 13, choose \(B_1\subseteq B\) s.t. \(\mu (B_1\times [a,b])=0\), \(\mu (B_1\times \mathbb R)\ne 0\), and so that for all \(x\in B_1\)
-
\(\mu _x\sim \mu _{\kappa (x)}\circ \kappa _\varPhi \) for every \(\mathfrak G[B]\)-holonomy \(\kappa \);
-
\(\mu _x(\{x\}\times [a,b])=0\);
-
\(\mu _x(\{x\}\times (s-\varepsilon ,s+\varepsilon ))>0\).
Next we choose some \(t<s\) and some \(A\subset B_1\) such that \(\mu (A\times \mathbb R)\ne 0\) and so that on top of the three bullets above, every \(x\in A\) also satisfies
-
\(\mu _x(\{x\}\times (t-\varepsilon ,t+\varepsilon ))=0\).
Here is how to do this. Let \(t:=s-(\frac{a+b}{2}-s)\equiv 2s-\frac{a+b}{2}\). We claim that
Indeed, if this were not the case, then by ergodicity there would exist some \(\mathfrak G\)-holonomy \(\kappa \) and some \(B'_1\subset B_1\) such that \(\kappa _\varPhi (B'_1\times (t-\varepsilon ,t+\varepsilon ))\cap (B\times (s-\varepsilon ,s+\varepsilon ))\) has positive measure. In this case, there would also exist some \(B''_1\subset B_1\) with \(\mu (B''_1\times \mathbb R)\ne 0\) such that for all \(x\in B''\),
So \(\kappa _\varPhi \) maps \(B''_1\times (s-\varepsilon ,s+\varepsilon )\) into \(B\times (2s-t-3\varepsilon ,2s-t+3\varepsilon )\subset B\times [a,b]\). But this is impossible, since \(\kappa _\varPhi \) is measure preserving, \(\mu (B\times [a,b])=0\), and
(\(\nu (B_1'')\ne 0\) because \(\mu (B_1''\times \mathbb R)\ne 0\)). Now that we know (11), the existence of A follows from the fiber decomposition of \(\mu \).
Define \(a':=t-\varepsilon \), \(b':=t+\varepsilon \), and choose \([\alpha ,\beta ]\subset (s-\varepsilon ,s+\varepsilon )\) such that \(\mu (A\times [\alpha ,\beta ])>0\) and \( |\alpha -\beta |<\frac{1}{3}\varepsilon \). Necessarily
Indeed, \(|a'-b'|=2\varepsilon \), \(|a-b|>6\varepsilon \), \(|a-\beta |>a-s-\varepsilon \ge \varepsilon \), and \(|b'-\alpha |>(s-\varepsilon )-(t+\varepsilon )=(s-t)-2\varepsilon =(\frac{a+b}{2}-s)-2\varepsilon >(\frac{a+b}{2}-a)-2\varepsilon =\frac{|a-b|}{2}-2\varepsilon \ge \varepsilon \).
We show that \( W:=A\times [\alpha ,\beta ] \) satisfies the requirements of step 1. Define
Recall that \(\mathfrak G[A]:=\mathfrak G\cap A^2\), and fix some \(\mathfrak G[A]\)-holonomy \(\kappa \). If \(x\in A\cap \mathrm {dom}(\kappa )\), \(x':=\kappa (x)\in A\) and \(|\varPhi (x,x')|<|\alpha -\beta |\), then
So \(\varPhi (x,x')\le U(x')-U(x)\). Exchanging the places of \(x,x'\) and noting that \(\varPhi (x',x)=-\varPhi (x,x')\), we find that \(\varPhi (x,x')=U(x')-U(x)\).
It follows that the function \(F(x,\xi ):=\xi -U(x)\) is invariant with respect to the induced equivalence relation \(\mathfrak G_\varPhi [W]\). By Lemma 9, this equivalence relation is ergodic. So \( \xi -U(x)=const\,\mu \text {--a.e. in }W. \)
The step follows with \(u_0(x):=U(x)+\mathrm {const.\,}\)
Step 2: Either \(A\times \mathbb R=\{(x,u_0(x)):x\in A\}\mod \mu \) and \(H_\mu =\{0\}\), or there exists \(c>0\) s.t. \(A\times \mathbb R=\{(x,u_0(x)+cn):x\in A, n\in \mathbb Z\}\mod \mu \) and \(H_\mu =c\mathbb Z\). In both cases, \( \varPhi (x,y)+u_0(x)-u_0(y)\in H_\mu \, \mu \text {--a.e. in }\mathfrak G_\varPhi [A\times \mathbb R]. \)
Sketch of proof (see [49] for details). Let
Notice that \(\mu _x[\{x\}\times (u_0(x),u_1(x))]=0\), and if \(u_1(x)<\infty \) then
Suppose \(((x,\xi ),(x',\eta ))\in \mathfrak G_\varPhi [W]\) and let \(\kappa \) be a \(\mathfrak G\)-holonomy such that \((x',\eta )=\kappa _\varPhi (x,\xi )\). Since \(\mu _{\kappa (x)}\circ \kappa _\varPhi =\mu _x\), \(u_1(x')<\infty \) iff \(u_1(x)<\infty \), and in this case, the identity \(u_0(x')=u_0(x)+\varPhi (x,x')\) implies that
It follows that \(u_1(x')=u_1(x)+\varPhi (x,x').\)
Recall that \(u_0(x')=u_0(x)+\varPhi (x,x')\), then \(u_1(x')-u_0(x')=u_1(x)-u_0(x)\), proving that \(u_1-u_0\) is \(\mathfrak G_\varPhi [W]\)-invariant. By ergodicity, either \(u_1<\infty \) \(\mu \)–a.e. in W and then \(u_1=u_0+\mathrm {const.\,}\), or \(u_1=\infty \) \(\mu \)–a.e. in W. Because \(\mu |_W\sim \int _A \delta _{(x,u_0(x))}d\nu (x)\), instead of saying “\(\mu \)–a.e. in W” we can say “\(\nu \)–a.e. in A.” In summary: \( u_1=u_0+c\,\nu \text {--a.e. in }A\text {, where }c\in [0,\infty ]. \)
We claim that \(c>0\). By step 1, for every \(x\in A\), \(\mu _x\) has a single atom in \(\{x\}\times [\alpha ,\beta ]\) (at \((x,u_0(x))\)). So \(u_0(x)\le \beta \le u_1(x)\), and the only way for c to be equal to zero is to have \(u_0(x)=u_1(x)=\beta \). If this is the case, then
But then by ergodicity, we can find \(A'\subset A\) such that \(\mu (A\times (\beta ,\beta +|\alpha -\beta |))>0\) and a \(\mathfrak G\)-holonomy \(\kappa \) such that \(\kappa (A')\subset A\) and \(|\alpha -\beta |<\varPhi (x,\kappa (x))<0\) on \(A'\). But this is absurd because in this case, \(\kappa _\varPhi \) maps \(A\times \{\beta \}\) into \(A\times [\alpha ,\beta )\) which has zero measure by the assumption that \(u_0=\beta \) on W.
We now separate cases.
Case 1: \(u_1<\infty \) \(\nu \)–a.e. in A.
In this case, a similar argument to the one we just used shows that for \(\nu \)–a.e. every \(x\in A\), \(\mu _x(\{x\}\times (u_1(x),u_1(x)+\delta ))=0\) for all \(\delta \) small enough. So \((x,u_1(x))=(x,u_0(x)+c)\) is an atom of \(\mu _x\). Since \(\mu _x(x,u_0(x))>0\) and \(\mu _x(x,u_0(x)+c)>0\) for \(\nu \)–a.e. \(x\in A\), \(\mu \) and \(\mu \circ g^c\) are not mutually singular. So \(c\in H_\mu \).
Similarly, since \(\mu _x(\{x\}\times (u_0(x),u_0(x)+c))=\mu _x(\{x\}\times (u_0(x),u_1(x)))=0\) for \(\nu \)–a.e. \(x\in A\), \(\mu \not \sim \mu \circ g^\tau \) for \(0<\tau <c\). So \(H_\mu =c\mathbb Z\).
Since \(\mu _x(\{x\}\times (u_0(x),u_0(x)+c))=0\), \(\mu _x(x,u_0(x))>0\), and \(\mu _x(x,u_0(x)+c)>0\) for \(\nu \)–a.e. \(x\in A\), \(\mu _x\sim \sum _{k\in \mathbb Z}\delta _{(x,u_0(x)+kc)}\) for a.e. \(x\in A\). It follows that
The \(\mathfrak G_\varPhi \)-invariance of \(\mu \) now implies that for a.e. \((x,\xi )\in A\times \mathbb R\), for all (countably many) \((y,\eta )\in A\times \mathbb R\) s.t. \(((x,\xi ),(y,\eta ))\in \mathfrak G_\varPhi [A\times \mathbb R]\),
whence \(\varPhi (x,y)+u_0(x)-u_0(y)\in c\mathbb Z\). In other words, \(\varPhi (x,y)+u_0(x)-u_0(y)\in H_\mu \) a.e. in \(\mathfrak G_\varPhi [A\times \mathbb R]\).
Case 2: \(u_1=\infty \) \(\nu \)–a.e. in A
In this case, \(\mu _x(\{x\}\times (u_0(x),\infty ))=0\) but \(\mu _x(x,u_0(x))>0\) \(\nu \)-a.e. in A.
We claim that \(\mu _x((-\infty ,u_0(x))=0\) \(\nu \)–a.e. in A. The argument is similar to the one we used before, so we only sketch it: Had there been some mass below the graph of \(u_0\) on A, then by ergodicity there would be some \(\mathfrak G_\varPhi \)-holonomy which maps a positive measure part of \(A\times \mathbb R\) into \(A\times \mathbb R\) in such a way that \(\varPhi \) takes strictly positive values. This holonomy would shift some positive measure piece of the graph of \(u_0\) strictly up in a measure preserving way. But this is impossible because there is no mass above the graph of \(u_0\).
Thus \(A\times \mathbb R=\{(x,u_0(x)):x\in A\}\mod \mu \). It automatically follows that \(H_\mu =\{0\}\). Again, this implies that \(\varPhi (x,y)+u_0(x)-u_0(y)=0\) a.e. in \(\mathfrak G_\varPhi [A\times \mathbb R]\). \(\square \)
Step 3: There exists \(u:X\rightarrow \mathbb R\) measurable s.t. \(X\times \mathbb R=\{(x,\xi ):\xi \in u(x)+H_\mu \}\mod \mu \) and \(\varPhi (x,y)+u(x)-u(y)\in H_\mu \) \(\mu \)-almost everywhere in \(\mathfrak G\).
Proof. Define \(F_0:A\rightarrow \mathbb R/H_\mu \) by \(F_0(x,\xi ):=u_0(x)+H_\mu \).
We can extend \(F_0\) to \( \mathrm {Sat}(A)=\{y\in X:\exists x\in A\text { s.t. }(x,y)\in \mathfrak G\} \) by setting
The definition is proper, because if \(x_1,x_2\in A\) both satisfy \((x_i,y)\in \mathfrak G\), then
By construction, \(F=F_0\) on A and for every \(x\in \mathrm {Sat}(A)\), for every y s.t. \((x,y)\in \mathfrak G\),
Let \(C:\mathbb R/H_\mu \rightarrow \mathbb R\) be a measurable (even piecewise continuous) function such that \(C(\tau +H_\mu )\in \tau +H_\mu \), and let
Then \(\varPhi (x,y)+u(x)-u(y)\in H_\mu \) a.e. in \(\mathfrak G_\varPhi \).
It immediately follows that \(G(x,\xi ):=\xi -u(x)+H_\mu \) is \(\mathfrak G_\varPhi \)-invariant, whence a.e. constant. The constant is zero because \(G=H_\mu \) on the positive measure set \(A\times [\alpha ,\beta ]\). So \(\xi -u(x)\in H_\mu \) \(\mu \)-a.e., whence \(X\times \mathbb R=\{(x,\xi ):\xi \in u(x)+H_\mu \}\). \(\Box \)
1.5 7.5 Notes and References
The cocycle reduction theorem is taken from [49], as is the proof sketched above. Extensions to cocycles taking values in non-abelian groups are given in [45].
Rights and permissions
Copyright information
© 2019 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Sarig, O. (2019). Horocycle Flows on Surfaces with Infinite Genus. In: Dani, S., Ghosh, A. (eds) Geometric and Ergodic Aspects of Group Actions. Infosys Science Foundation Series(). Springer, Singapore. https://doi.org/10.1007/978-981-15-0683-3_2
Download citation
DOI: https://doi.org/10.1007/978-981-15-0683-3_2
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-15-0682-6
Online ISBN: 978-981-15-0683-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)






 .
.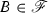 , then
, then 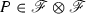 , then
, then